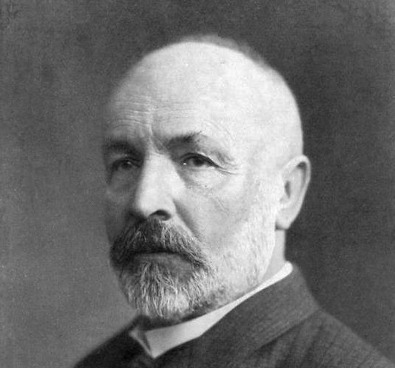


- Les ensembles
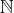 et
et 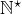 sont-ils équipotents ?
sont-ils équipotents ? - Les ensembles
![Rendered by QuickLaTeX.com ]0,1[](https://math-os.com/wp-content/ql-cache/quicklatex.com-82fba134bd9b6970cdfc90cf14ad8f7b_l3.png) et
et  sont-ils équipotents ?
sont-ils équipotents ? - Les ensembles
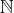 et
et 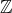 sont-ils équipotents ?
sont-ils équipotents ? - Les ensembles
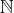 et
et 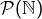 sont-ils équipotents ?
sont-ils équipotents ?
Lorsque les ensembles E et F sont finis, le fait qu’ils soient équipotents équivaut à l’égalité de leurs cardinaux. Cette notion exprime donc de manière précise l’idée que deux ensembles – finis ou non – sont « de même taille ».
Commençons par une simple observation…
1 – Accouplement de deux bijections
Considérons deux ensembles ![]() disjoints, deux ensembles
disjoints, deux ensembles ![]() disjoints et supposons l’existence d’une bijection
disjoints et supposons l’existence d’une bijection ![]() et d’une bijection
et d’une bijection ![]() .
.
Il est alors facile de construire une bijection ![]() , en posant :
, en posant :
![Rendered by QuickLaTeX.com \[\boxed{h:A\cup B\to A'\cup B',\,x\mapsto\left\{\begin{array}{cc}f(x) & \text{si }x\in A\\g(x) & \text{si }x\in B\\\end{array}\right.}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-099d160e8f930175fc55aae2bef0cccb_l3.png)
Pour justifier le caractère bijectif de ![]() , le plus simple est de considérer l’application :
, le plus simple est de considérer l’application :
![]()
et de constater que :
![]()
La première égalité montre notamment que ![]() est injective, et la seconde que
est injective, et la seconde que ![]() est surjective.
est surjective.
2 – Une histoire de point fixe
Rappelons pour commencer qu’étant donnés un ensemble ![]() et une application
et une application ![]() , on appelle point fixe de
, on appelle point fixe de ![]() tout élément
tout élément ![]() vérifiant
vérifiant ![]() .
.
La proposition suivante est un cas particulier d’un résultat connu sous le nom de théorème de Knaster-Tarski. Elle va jouer un rôle-clef dans la preuve que nous verrons du théorème de CBS. Historiquement, ce résultat est apparu en 1928 sous la plume de B. Knaster (1893-1980), mais sous une forme restreinte, puis généralisé en 1955 par A. Tarski (1901-1983).
Proposition
Soit ![]() un ensemble et soit
un ensemble et soit ![]() une application croissante au sens de l’inclusion, c’est-à-dire vérifiant :
une application croissante au sens de l’inclusion, c’est-à-dire vérifiant :
![]()
Alors ![]() possède au moins un point fixe.
possède au moins un point fixe.
Cliquer pour voir / masquer la preuve
Notons ![]() l’ensemble des parties de
l’ensemble des parties de ![]() qui contiennent leur image :
qui contiennent leur image :
![]()
Comme ![]() , on voit déjà que
, on voit déjà que ![]() . Considérons alors :
. Considérons alors :
![]()
Si ![]() , alors
, alors ![]() , car l’intersection d’une famille
, car l’intersection d’une famille ![]() d’ensembles est contenue dans
d’ensembles est contenue dans ![]() pour tout
pour tout ![]() .
.
Par croissance de ![]() , il en résulte que
, il en résulte que ![]() et donc (vu que
et donc (vu que ![]() et par transitivité de l’inclusion) :
et par transitivité de l’inclusion) : ![]() Comme cette dernière inclusion vaut pour tout
Comme cette dernière inclusion vaut pour tout ![]() , il s’ensuit que
, il s’ensuit que ![]() .
.
On a déjà établi une première inclusion. Comme ![]() est croissante, on en déduit que
est croissante, on en déduit que ![]() , ce qui signifie exactement que
, ce qui signifie exactement que ![]() , et ceci entraîne que
, et ceci entraîne que ![]() .
.
Il est maintenant prouvé que ![]() est un point fixe de
est un point fixe de ![]() .
.
Remarque – on aurait pu conclure tout aussi bien en considérant plutôt :
![]()
![]()
Le détail de cette preuve alternative (mais très similaire) est laissé au lecteur 🙂
3 – Le théorème de Cantor-Bernstein-Schröder
Comme annoncé dans l’introduction, il s’agit du résultat suivant :
Théorème CBS
Soient ![]() ,
, ![]() des ensembles.
des ensembles.
On suppose qu’il existe une injection ![]() et une injection
et une injection ![]() .
.
Dans ces conditions, ![]() et
et ![]() sont équipotents.
sont équipotents.
Cliquer pour voir / masquer la preuve
Pour lire ce qui suit, vous aurez notamment besoin d’être à l’aise avec les notions d’image directe et d’image réciproque. A toutes fins utiles, je vous signale cet article, qui expose ces notions fondamentales en partant de zéro.
Commençons par observer qu’étant donnée une application ![]() , l’application
, l’application
![]()
![]()
Considérons alors l’application :
![Rendered by QuickLaTeX.com \[\boxed{\begin{array}{cccc}c\,: & \mathcal{P}(E) & \to & \mathcal{P}(E)\\& A & \mapsto & E-\beta\left<F-\alpha\left<A\right>\right>\end{array}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-43f6e2fb45ebe86d37fd970c59e7010f_l3.png)
On constate (grâce aux propriétés ![]() et
et ![]() ) que
) que ![]() est croissante pour l’inclusion et possède donc (d’après la proposition de la section 2) un point fixe
est croissante pour l’inclusion et possède donc (d’après la proposition de la section 2) un point fixe ![]() . On a donc :
. On a donc :
![]()
c’est-à-dire :
![]()
On dispose alors de la bijection
![]()
et de la bijection
![]()
La notation ![]() est valable (bien que
est valable (bien que ![]() ne soit pas supposée bijective) puisque, d’après
ne soit pas supposée bijective) puisque, d’après ![]() , tout élément de
, tout élément de ![]() possède un antécédent par
possède un antécédent par ![]() (antécédent unique, en raison de l’injectivité de
(antécédent unique, en raison de l’injectivité de ![]() ).
).
Il ne reste alors plus qu’à accoupler ![]() et
et ![]() , comme expliqué à la section 1, pour obtenir une bijection de
, comme expliqué à la section 1, pour obtenir une bijection de ![]() vers
vers ![]() .
.
Corollaire
Il est clair que si ![]() ,
, ![]() et
et ![]() sont trois ensembles finis tels que
sont trois ensembles finis tels que ![]() et si de plus
et si de plus ![]() , alors
, alors ![]() .
.
Que reste-t-il de cette affirmation en remplaçant finis par infinis et l’hypothèse d’égalité des cardinaux par celle d’équipotence de ![]() et
et ![]() ?
?
Sous ces hypothèses modifiées, la conclusion ne persiste pas (contre-exemple : ![]() et l’application
et l’application ![]() est bijective, mais les deux inclusions sont strictes !) mais on peut tout de même dire que
est bijective, mais les deux inclusions sont strictes !) mais on peut tout de même dire que ![]() ,
, ![]() et
et ![]() sont équipotents.
sont équipotents.
En effet, l’inclusion ![]() montre l’existence d’une injection
montre l’existence d’une injection ![]() . Il existe, de même, une injection
. Il existe, de même, une injection ![]() et donc (vu que
et donc (vu que ![]() et
et ![]() sont équipotents par hypothèse) un injection
sont équipotents par hypothèse) un injection ![]() . On termine en invoquant le théorème CBS.
. On termine en invoquant le théorème CBS.
4 – L’ensemble  des rationnels est dénombrable
des rationnels est dénombrable
Il nous suffit de construire une injection de ![]() dans
dans ![]() . Lorsque ce sera fait, il restera à :
. Lorsque ce sera fait, il restera à :
- remarquer qu’il existe évidemment une injection en sens inverse (puisque
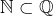 ),
), - appliquer le théorème CBS.
On sait que tout nombre rationnel ![]() peut s’écrire, de manière unique sous la forme :
peut s’écrire, de manière unique sous la forme :
![]()
![Rendered by QuickLaTeX.com \[\boxed{\begin{array}{ccccccc}f\,: & \mathbb{Q} & \to & \mathbb{N}, & r & \mapsto & \left\{\begin{array}{cc}2^{N(r)}\,3^{D(r)} & \text{si }N(r)\geqslant0\\2^{N(r)}\,3^{D(r)}\,5 & \text{sinon}\end{array}\right.\end{array}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d1042950ca6bc8a383297f67985c8181_l3.png)
![]() est injective, en raison de l’unicité de la décomposition en facteurs premiers d’un entier naturel plus grand que 1, ce qui prouve le résultat annoncé.
est injective, en raison de l’unicité de la décomposition en facteurs premiers d’un entier naturel plus grand que 1, ce qui prouve le résultat annoncé.
Cette démonstration repose sur une astuce arithmétique, que l’on retrouve sous une forme similaire dans une preuve courte de la dénombrabilité de ![]() . Les détails sont accessibles en dépliant le paragraphe ci-dessous.
. Les détails sont accessibles en dépliant le paragraphe ci-dessous.
Une preuve courte de la dénombrabilité de 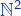 (cliquer pour déplier / replier)
(cliquer pour déplier / replier)
L’application ![]() est bijective. En effet :
est bijective. En effet :
- Soient
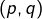 et
et 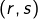 deux couples d’entiers naturels tels que
deux couples d’entiers naturels tels que 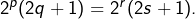 En supposant
En supposant 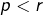 , on aurait
, on aurait 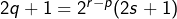 , ce qui est absurde puisque le membre de gauche de cette égalité est impair, tandis que son membre de droite est pair. Pour la même raison, l’hypothèse
, ce qui est absurde puisque le membre de gauche de cette égalité est impair, tandis que son membre de droite est pair. Pour la même raison, l’hypothèse 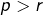 ne tient pas et donc
ne tient pas et donc 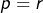 . Il s’ensuit que
. Il s’ensuit que 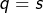 et finalement que
et finalement que 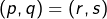 . Ceci montre que
. Ceci montre que  est injective.
est injective. - D’évidence :
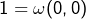 . Et si
. Et si 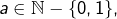 alors on voit en décomposant
alors on voit en décomposant  en produit de facteurs premiers qu’il existe
en produit de facteurs premiers qu’il existe 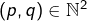 tel que
tel que 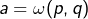 (il suffit de regrouper les facteurs premiers impairs).
(il suffit de regrouper les facteurs premiers impairs).
Ainsi, ![]() et
et ![]() sont équipotents. Comme
sont équipotents. Comme ![]() et
et ![]() sont équipotents (évident : considérer la bijection
sont équipotents (évident : considérer la bijection ![]() ), il s’ensuit que
), il s’ensuit que ![]() et
et ![]() sont équipotents.
sont équipotents.
Noter qu’il existe d’autres façons d’établir ce résultat. Le dessin ci-dessous doit pouvoir vous inspirer (solution en annexe) :
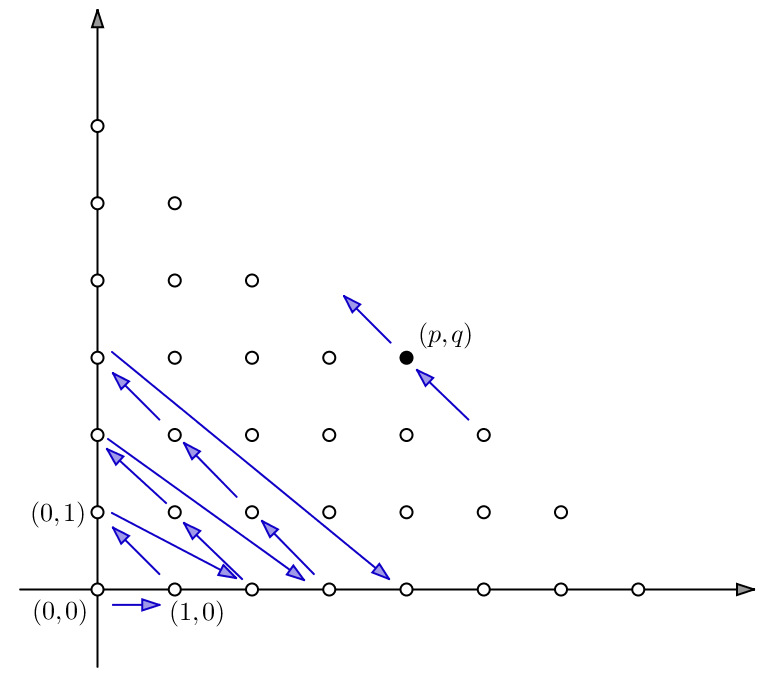
5 – Equipotence de  et
et 
![]()
![]()
![Rendered by QuickLaTeX.com \[\delta(b)=\sum_{n=0}^\infty\frac{b_n}{2^n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f9819ab9509c3cfc318c45b8f30abcb4_l3.png)
![Rendered by QuickLaTeX.com \[\frac12=\sum_{n=2}^\infty\frac{1}{2^n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b0d3fdf08f8044e6897bdefd0778cb50_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\begin{array}{cccc}\psi\,: & \{0,1\}^\mathbb{N} & \to & \mathbb{R}\\\\& b & \mapsto & \displaystyle{\sum_{n=0}^\infty\frac{b_n}{3^n}}\end{array}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-37290a00269f754d4c3987d280885063_l3.png)
![]()
![]()
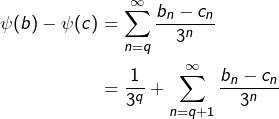
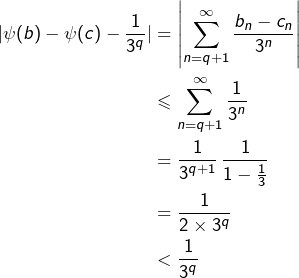
6 – Equipotence de  et
et 
Théorème
Pour cela, nous aurons besoin du :
Lemme
Si ![]() est un ensemble infini tel que
est un ensemble infini tel que ![]() , alors
, alors ![]() .
.
Remarque
Ce lemme n’est plus valable si ![]() est supposé fini.
est supposé fini.
En effet, si ![]() , alors
, alors ![]() donc
donc ![]() .
.
Pourtant
![]()
Signalons, avant de démontrer ce lemme, puis ce théorème, qu’il y a quelque chose de redondant dans l’énoncé de chacun d’eux, à savoir l’hypothèse ![]() . On peut en effet prouver que cette condition est vérifiée par tout ensemble infini (cela exige l’usage de l’axiome du choix). Mais nous n’allons pas détailler ce point et nous contenter de ces énoncés.
. On peut en effet prouver que cette condition est vérifiée par tout ensemble infini (cela exige l’usage de l’axiome du choix). Mais nous n’allons pas détailler ce point et nous contenter de ces énoncés.
Preuve du lemme (cliquer pour déplier / replier)
D’une manière générale, et pour tout ensemble ![]() , l’application
, l’application ![]() est injective. En particulier, il existe une injection de
est injective. En particulier, il existe une injection de ![]() dans
dans ![]() .
.
Montrons l’existence d’une injection en sens inverse.
Comme ![]() est infini (puisque
est infini (puisque ![]() est infini et que
est infini et que ![]() est injective), alors
est injective), alors ![]() . Il en résulte que
. Il en résulte que ![]() . Il suffit donc d’établir l’existence d’une injection
. Il suffit donc d’établir l’existence d’une injection ![]() . Or, par hypothèse, il existe une injection
. Or, par hypothèse, il existe une injection ![]() . Considérons l’application :
. Considérons l’application :
![]()
Soient ![]() et
et ![]() deux couples de parties non vides de
deux couples de parties non vides de ![]() , tels que
, tels que ![]() . Soient
. Soient ![]() et
et ![]() ; alors
; alors ![]() , donc il existe
, donc il existe ![]() tel que
tel que ![]() . Vue l’injectivité de
. Vue l’injectivité de ![]() , ceci impose
, ceci impose ![]() , d’où en particulier
, d’où en particulier ![]() et
et ![]() . On a montré que
. On a montré que ![]() et
et ![]() . Pour des raisons évidentes de symétrie, ces inclusions sont en fait des égalités.
. Pour des raisons évidentes de symétrie, ces inclusions sont en fait des égalités.
On a établi l’existence d’une injection de ![]() dans
dans ![]() et d’une injection de
et d’une injection de ![]() dans
dans ![]() . Il reste à invoquer le théorème CBS pour conclure.
. Il reste à invoquer le théorème CBS pour conclure.
Preuve du théorème (cliquer pour déplier / replier)
Notons 0 et 1 deux éléments distincts de A. L’application :
![]()
Par ailleurs, si l’on note ![]() le graphe de
le graphe de ![]() , alors l’application
, alors l’application
![]()
Or ![]() (il est en effet facile de voir que si
(il est en effet facile de voir que si ![]() , alors
, alors ![]() ), donc il existe une injection
), donc il existe une injection ![]() .
.
A nouveau, le théorème CBS donne la conclusion.
Comme l’indique le titre de cette section, nous souhaitons prouver que ![]() et
et ![]() sont équipotents. D’après le théorème ci-dessus, il suffit d’expliquer pourquoi
sont équipotents. D’après le théorème ci-dessus, il suffit d’expliquer pourquoi ![]() et
et ![]() sont équipotents. Proposons deux points de vue :
sont équipotents. Proposons deux points de vue :
1er point de vue
2ème point de vue
![Rendered by QuickLaTeX.com \[M(x,y)=\sum_{i=1}^\infty\frac{x_i}{10^{2i-1}}+\sum_{i=1}^\infty\frac{y_i}{10^{2i}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-dc8123e07a406f943e8bf947cce8c2a2_l3.png)
![]()
Annexe : une preuve géométrique de la dénombrabilité de 
Le dessin doit suggérer qu’on énumère les couples d’entiers naturels par diagonales successives :
- sur la première diagonale, il n’y a que
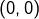 ,
, - sur la seconde, on trouve
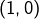 puis
puis 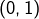 ,
, - sur la troisième, on trouve successivement
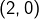 ,
, 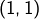 puis
puis 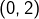 ,
, - etc …
Sur chaque « diagonale », les couples partagent une propriété commune : la somme des coordonnées est fixe. Par conséquent, le couple générique ![]() appartient à la diagonale qui commence par
appartient à la diagonale qui commence par ![]() .
.
Et ce point ![]() est précédè par
est précédè par ![]() , qui termine la diagonale précédente.
, qui termine la diagonale précédente.
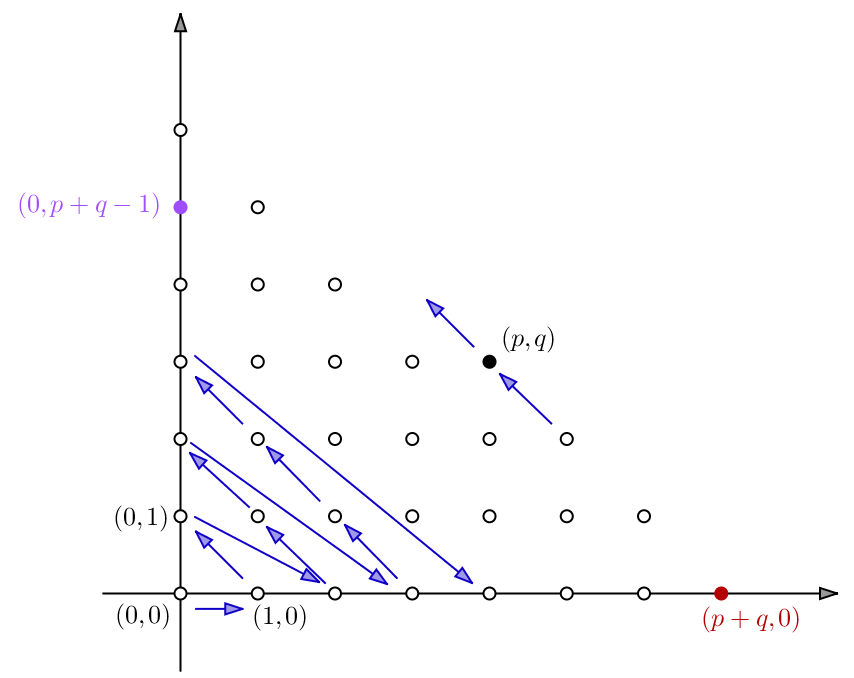
Les points ![]() ,
, ![]() ,
, ![]() ,
, ![]() , … portent les numéros d’ordre 0, 1, 2, 3 …
, … portent les numéros d’ordre 0, 1, 2, 3 …
Quel est, dans ces conditions, le numéro d’ordre de ![]() ?
?
Il n’est pas difficile de voir que les diagonales successives comportent un nombre croissant de couples : un couple pour la première, deux pour la suivante, puis trois etc …
Si l’on prend en compte toutes les diagonales depuis la toute première jusqu’à la diagonale précédent celle qui porte le couple ![]() , on totalise un nombre de couples égal à :
, on totalise un nombre de couples égal à :
![]()
Il reste à ajouter les couples ![]() , …,
, …, ![]() , qui sont au nombre de
, qui sont au nombre de ![]() . Finalement, nous avons deviné la formule qui donne le numéro d’ordre du couple générique
. Finalement, nous avons deviné la formule qui donne le numéro d’ordre du couple générique ![]() et qui, par là-même, nous donne explicitement une bijection de
et qui, par là-même, nous donne explicitement une bijection de ![]() vers
vers ![]() :
:
![]()
Il reste à vérifier proprement que cette application ![]() est effectivement une bijection (et, cerise sur le gateau, à expliciter sa bijection réciproque), mais cela, je vous le laisse en exercice 🙂
est effectivement une bijection (et, cerise sur le gateau, à expliciter sa bijection réciproque), mais cela, je vous le laisse en exercice 🙂
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.



Excellent travail