
1 – Description informelle de la notion de bijection
C’est décidé, je fais expertiser ma collection de livres anciens !
Pour préparer le terrain, il faut étiqueter chaque bouquin et lui attribuer ainsi un numéro d’ordre.
Comme je dispose justement d’un ensemble d’étiquettes (avec un numéro inscrit sur chacune d’elles), ça va être un jeu d’enfant. Mais attention, cet étiquetage doit être « parfait » au sens suivant :
- condition 1 : deux livres distincts ne doivent pas correspondre au même numéro
- condition 2 : chaque numéro doit correspondre à un livre
Dans le jargon des mathématiciens, on exprime cela en disant que :
L’application de l’ensemble X des livres vers l’ensemble Y des numéros qui, à chaque livre associe son numéro, doit être bijective.
Expliquons un peu cette étrange terminologie…
En associant, à chaque livre ![]() de ma collection, un numéro n bien déterminé, je définis une application
de ma collection, un numéro n bien déterminé, je définis une application ![]() de
de ![]() vers
vers ![]()
Afin d’expliciter ce lien, on peut noter : ![]() On dit que
On dit que ![]() est l’image de
est l’image de ![]() par
par ![]() ou (de manière équivalente) que
ou (de manière équivalente) que ![]() est un antécédent de
est un antécédent de ![]() par
par ![]()
En clair, ![]() désigne le numéro inscrit sur l’étiquette portée par le livre
désigne le numéro inscrit sur l’étiquette portée par le livre ![]()
- Si la condition 1 ci-dessus est remplie, on dit que l’application f est injective.
- Si la condition 2 est satisfaite, on dit que f est surjective.
Et si f est à la fois injective et surjective, on dit qu’elle est bijective (ou que c’est une bijection) : cela signifie que chaque numéro possède un unique antécédent par f, autrement dit, chaque numéro identifie un livre et un seul.
Evidemment, ce qui précède peut être généralisé à des ensembles ![]() et
et ![]() absolument quelconques (le terme ensemble désigne une collection d’objets, sans plus de précision : c’est un peu naïf mais on s’en contentera).
absolument quelconques (le terme ensemble désigne une collection d’objets, sans plus de précision : c’est un peu naïf mais on s’en contentera).
Etablir une bijection de ![]() vers
vers ![]() consiste donc à associer, à chaque élément de
consiste donc à associer, à chaque élément de ![]() un élément bien déterminé de
un élément bien déterminé de ![]() de telle sorte que :
de telle sorte que :
Tout élément de Y possède un unique antécédent dans X
Il peut être commode de représenter les ensembles par des « patates » et de dessiner une flèche joignant chaque élément de ![]() à son image dans
à son image dans ![]()
Le diagramme ci-dessous représente une bijection de l’ensemble
{« chien », « chat », « cheval », « lion », « lapin »}
vers l’ensemble
{« chienne », « chatte », « jument », « lionne », « hase »}
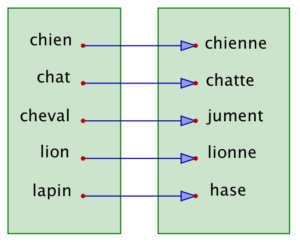
Cette bijection paraît naturelle : à chaque nom de mâle est associé le nom de la femelle correspondante.
Mais on pourrait imaginer autre chose… par exemple :
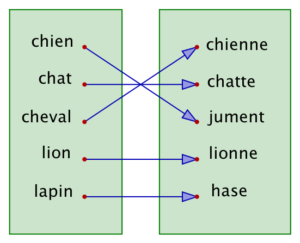
Moins naturel n’est-ce pas ? Et pourtant : j’ai simplement décidé de respecter l’ordre alphabétique ! Parmi les mots appartenant à l’ensemble de gauche, le premier dans l’ordre alphabétique est « chat »; pour cette raison, je décide de lui associer le mot « chatte » qui est, parmi les mots appartenant à l’ensemble de droite, le premier dans l’ordre alphabétique. De même pour le second (« cheval »), auquel j’associe le second (« chienne »). De même pour le troisième (« chien »), auquel j’associe le troisième (« jument »), etc… Vous avez compris.
Il n’y aucune raison de renoncer aux autres possibilités, sans d’ailleurs chercher à leur attribuer une quelconque logique (mâle → femelle, ordre alphabétique, ou autre…). On peut vérifier qu’il existe en tout 120 bijections entre ces deux ensembles. Pourquoi 120 ? Parce que c’est la « factorielle » de 5, c’est-à-dire le produit des entiers de 1 à 5. On peut en effet montrer, de façon générale, qu’étant donnés deux ensembles comportant chacun n éléments, il existe en tout et pour tout n! bijections de l’un vers l’autre.
Pour en savoir davantage au sujet de la factorielle d’un entier naturel, vous pouvez jeter un coup d’œil à cet autre article de vulgarisation.
Observons ce nouvel exemple :
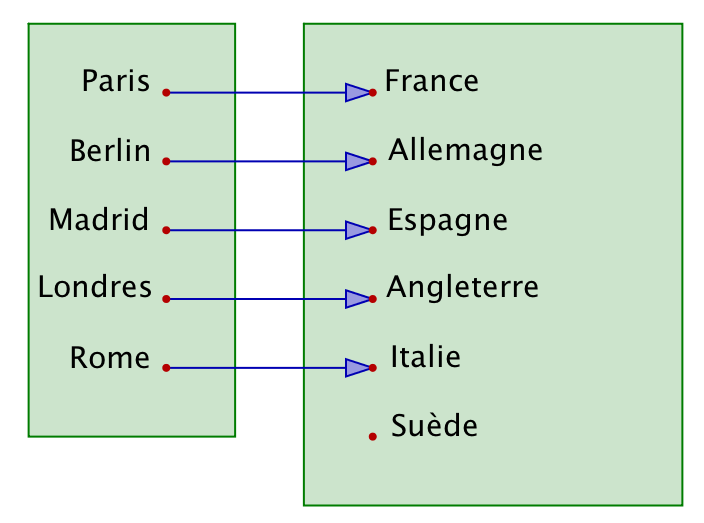
On a considéré ici un ensemble V de cinq noms de capitales européennes :
V = {« Paris », « Berlin », « Madrid », « Londres », « Rome »}
ainsi qu’un ensemble P de six pays européens :
P = {« France », « Allemagne », « Espagne », « Angleterre », « Italie », « Suède »}
A chaque ville, on a associé le pays dont elle est la capitale. Mais la capitale de la Suède n’apparaît pas dans V, et donc l’élément « Suède » ne possède aucun antécédent. En d’entre termes, notre application n’est pas surjective (et, en particulier, pas bijective).
Voyons autre chose …
• A ma gauche, l’ensemble ![]()
• A ma droite, l’ensemble ![]()
Si l’on associe à chaque élément de G le reste de sa division par 3, on obtient ceci :
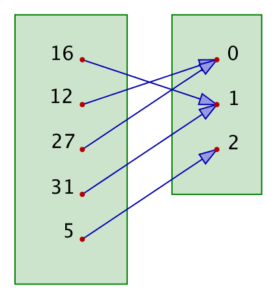
Ainsi, par exemple :
![]()
Cette fois, tous les éléments de l’ensemble de droite sont atteints, mais certains le sont plusieurs fois ! Il s’agit donc d’une application non injective; en particulier, ce n’est pas une bijection.
Pour une présentation plus formelle de ces notions (applications, injections, surjections et bijections), je vous propose de consulter les deux vidéos suivantes de la chaîne Math-OS :
2 – Composer des bijections
Il existe un moyen naturel permettant, à partir de deux applications quelconques, d’en fabriquer une troisième : c’est ce qu’on appelle la composition. De quoi s’agit-il ?
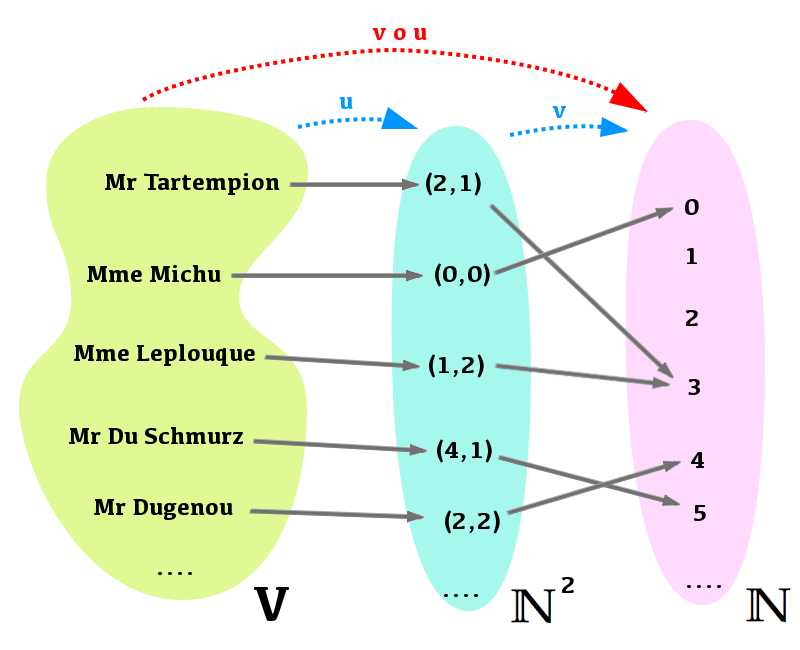
Imaginons l’ensemble ![]() des habitants d’un village et considérons l’application
des habitants d’un village et considérons l’application ![]() qui, à chacune de ces personnes, associe le couple
qui, à chacune de ces personnes, associe le couple ![]() où
où ![]() désigne le nombre de ses garçons et
désigne le nombre de ses garçons et ![]() le nombre de ses filles.
le nombre de ses filles.
Si par exemple Mr Tartempion appartient à ![]() et s’il a trois garçons et une fille, alors son image par
et s’il a trois garçons et une fille, alors son image par ![]() sera le couple
sera le couple ![]()
Considérons ensuite l’application ![]() qui, à tout couple
qui, à tout couple ![]() d’entiers naturels associe
d’entiers naturels associe ![]()
Il est alors possible de composer ![]() par
par ![]() : cela consiste, pour chaque habitant du village, à lui associer l’image par
: cela consiste, pour chaque habitant du village, à lui associer l’image par ![]() de son image par
de son image par ![]() Autrement dit, à chaque personne est associé le nombre de ses enfants.
Autrement dit, à chaque personne est associé le nombre de ses enfants.
Cette nouvelle application est notée ![]() (ce qui se lit «
(ce qui se lit « ![]() rond
rond ![]() »).
»).
Pour formaliser un peu, disons que si ![]() et
et ![]() sont deux applications quelconques, alors
sont deux applications quelconques, alors ![]() est définie par :
est définie par :
![]()
Signalons une propriété à la fois simple et très utile :
Proposition
Si ![]() et
et ![]() sont des bijections, alors c’est aussi le cas de
sont des bijections, alors c’est aussi le cas de ![]()
3 – Des bijections … d’accord, mais pour quoi faire ?
Vous l’aurez deviné en lisant la section 1 : étant donnés deux ensembles finis ![]() et
et ![]() , une condition nécessaire et suffisante pour qu’il soit possible d’établir une bijection (un « fléchage parfait ») de
, une condition nécessaire et suffisante pour qu’il soit possible d’établir une bijection (un « fléchage parfait ») de ![]() vers
vers ![]() est que ces deux ensembles possèdent le même nombre d’éléments (on dit aussi : le même cardinal).
est que ces deux ensembles possèdent le même nombre d’éléments (on dit aussi : le même cardinal).
Cette simple observation constitue l’une des principales clefs de la « combinatoire », domaine des mathématiques où l’on tâche de répondre à des questions du genre « combien tel ensemble fini possède-t-il d’éléments ? ». Donnons-en quelques illustrations.
Exemple 1 : nombre de parties d’un ensemble
Etant donné un ensemble de cardinal ![]() , une question naturelle consiste à déterminer le nombre de ses sous-ensembles. Ainsi, l’ensemble
, une question naturelle consiste à déterminer le nombre de ses sous-ensembles. Ainsi, l’ensemble ![]() possède huit sous-ensembles, à savoir :
possède huit sous-ensembles, à savoir :
- l’ensemble vide, noté
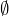
- les singletons
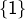 ,
, 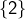 et
et 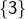 (ce sont les sous-ensembles de cardinal 1)
(ce sont les sous-ensembles de cardinal 1) - les paires
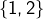 ,
, 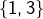 et
et 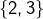 (ce sont les sous-ensembles de cardinal 2)
(ce sont les sous-ensembles de cardinal 2) - l’ensemble
 lui-même
lui-même
D’une manière générale, si ![]() est de cardinal
est de cardinal ![]() alors
alors ![]() possède exactement
possède exactement ![]() sous-ensembles. Trois preuves rigoureuses de cette affirmation sont rassemblées dans l’article « Combien un ensemble fini possède-t-il de parties ? ».
sous-ensembles. Trois preuves rigoureuses de cette affirmation sont rassemblées dans l’article « Combien un ensemble fini possède-t-il de parties ? ».
Sans détailler ici ces preuves un peu techniques, disons simplement que l’une d’elles consiste à établir une bijection entre l’ensemble des sous-ensembles de ![]() et un autre ensemble dont le cardinal est connu (et égal à
et un autre ensemble dont le cardinal est connu (et égal à ![]() ).
).
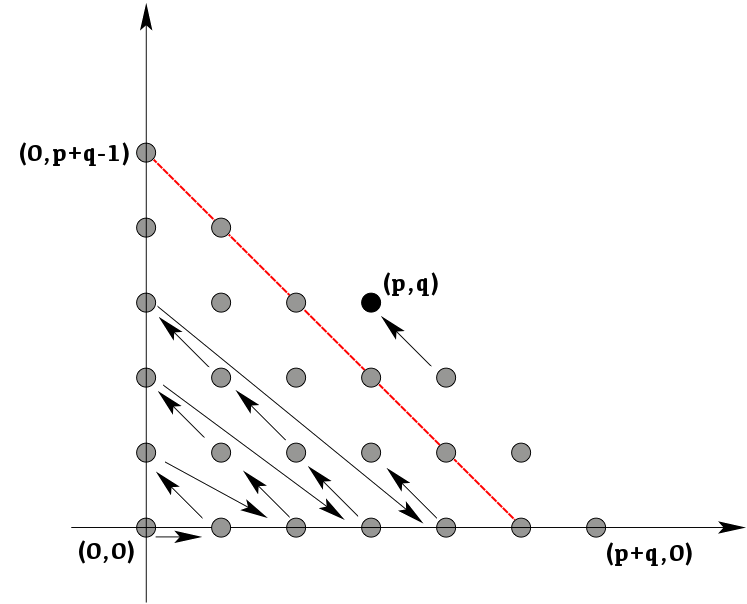
Exemple 2 : nombre de chemins dans un réseau carré
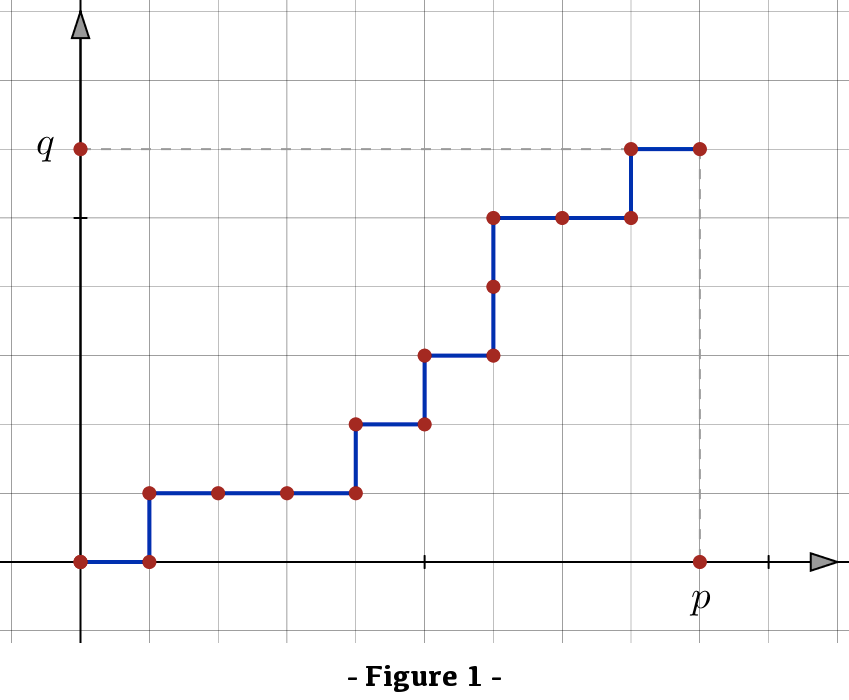
La figure 1 ci-dessous représente un système de coordonnées et un « chemin » joignant l’origine au point de coordonnées (entières positives) ![]() et
et ![]() On s’impose la règle du jeu suivante : en partant de l’origine, on ne peut se déplacer que vers la droite ou vers le haut, d’une unité dans les deux cas.
On s’impose la règle du jeu suivante : en partant de l’origine, on ne peut se déplacer que vers la droite ou vers le haut, d’une unité dans les deux cas.
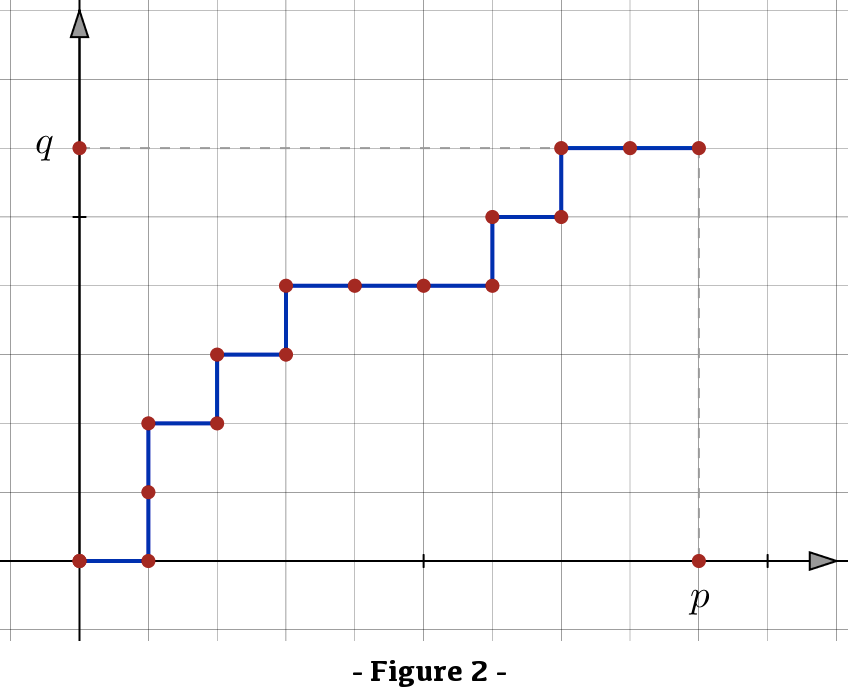
La figure 2 montre un autre chemin possible :
Le nombre de tels chemins dépend bien évidemment de ![]() et
et ![]() On peut le noter
On peut le noter ![]() afin de souligner cette dépendance. Mais par quelle formule peut-on calculer
afin de souligner cette dépendance. Mais par quelle formule peut-on calculer ![]() ?
?
Une manière de répondre consiste à associer à chaque chemin un mot de ![]() lettres, écrit dans un alphabet comportant seulement deux symboles : la lettre ‘D’ (pour indiquer un déplacement vers la droite d’une unité) et la lettre ‘H’ (pour indiquer un déplacement vers le haut d’une unité).
lettres, écrit dans un alphabet comportant seulement deux symboles : la lettre ‘D’ (pour indiquer un déplacement vers la droite d’une unité) et la lettre ‘H’ (pour indiquer un déplacement vers le haut d’une unité).
Ainsi, le chemin représenté à la figure 1 est associé au mot :
D H D D D H D H D H H D D H D
tandis que celui représenté à la figure 2 est associé au mot :
D H H D H D H D D D H D H D D
La connaissance d’un chemin particulier de ![]() vers
vers ![]() détermine un mot de longueur p + q, comportant p fois la lettre ‘D’ et q fois la lettre ‘H’.
détermine un mot de longueur p + q, comportant p fois la lettre ‘D’ et q fois la lettre ‘H’.
Réciproquement, chaque mot de ce type détermine un unique chemin : on voit ainsi apparaître une bijection entre l’ensemble des chemins et celui des mots ayant les caractéristiques précitées. Pour connaître le nombre de chemins, il suffit donc de calculer le nombre de mots.
Or il s’agit là d’une opération de routine : on peut imaginer un casier comportant p + q cases et compter le nombre de manières de choisir p cases parmi p + q (celles où l’on placera une lettre ‘D’). Une fois ce choix effectué, les cases restantes seront fatalement occupées par des lettres ‘H’.
Le nombre de façons de choisir k objets parmi n (sans répétition ni considération d’ordre) est classiquement donné par la formule suivante (le membre de gauche se lit k parmi n) :
![]()
Par conséquent, le nombre de chemins est :
![]()
Par exemple, si p = 3 et q = 2, le nombre de chemins est :
![]()
ce qu’on peut confirmer en énumérant « à la main » les différentes possibilités.
Et si p = 9 et q = 6, ce nombre passe à :
![]()
Au passage, il est intéressant de constater la puissance des méthodes combinatoires : elles donnent accès au calcul du cardinal d’un ensemble, tout en évitant l’énumération explicite de ses éléments (chose impossible à réaliser si ces éléments sont trop nombreux).
Exemple 3 : nombre d’opérations binaires transitives
Il arrive aussi que l’on peine à trouver une bijection entre l’ensemble fini dont on cherche le cardinal et un ensemble de cardinal connu. C’est ainsi que certaines questions de combinatoire, simples en apparence, restent à ce jour non résolues.
Etant donné un ensemble ![]() on est parfois conduit à munir cet ensemble d’une relation binaire, ce qui veut simplement dire que chaque élément de
on est parfois conduit à munir cet ensemble d’une relation binaire, ce qui veut simplement dire que chaque élément de ![]() est en relation avec zéro, un ou plusieurs autre(s). On peut visualiser une relation binaire en dessinant une flèche de
est en relation avec zéro, un ou plusieurs autre(s). On peut visualiser une relation binaire en dessinant une flèche de ![]() vers
vers ![]() lorsque
lorsque ![]() est en relation avec
est en relation avec ![]() Le diagramme ci-dessous représente une relation binaire sur un ensemble de cardinal
Le diagramme ci-dessous représente une relation binaire sur un ensemble de cardinal ![]() On y voit notamment que :
On y voit notamment que :
 est en relation avec
est en relation avec 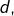
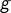 est en relation avec lui-même et avec
est en relation avec lui-même et avec  et avec
et avec 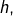
 n’est en relation avec aucun élément.
n’est en relation avec aucun élément.
Une relation binaire est dite transitive si, pour tout triplet ![]() d’éléments de
d’éléments de ![]() le fait que
le fait que ![]() soit en relation avec
soit en relation avec ![]() et que
et que ![]() soit en relation avec
soit en relation avec ![]() entraîne que
entraîne que ![]() est en relation avec
est en relation avec ![]()
Par exemple, dans l’ensemble ![]() on peut définir la relation de divisibilité : étant donnés deux entiers
on peut définir la relation de divisibilité : étant donnés deux entiers ![]() et
et ![]() appartenant à
appartenant à ![]() on dit que «
on dit que « ![]() divise
divise ![]() » lorsqu’il existe un entier naturel
» lorsqu’il existe un entier naturel ![]() tel que
tel que ![]() (on dit aussi que «
(on dit aussi que « ![]() est multiple de
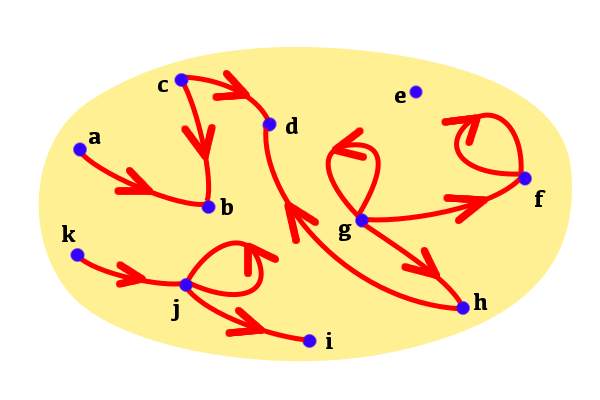
est multiple de ![]() »). En voici une représentation graphique (afin de ne pas surcharger la figure, les pointes des flèches n’ont pas été représentées, mais il n’y a aucun doute quant à leur orientation) :
»). En voici une représentation graphique (afin de ne pas surcharger la figure, les pointes des flèches n’ont pas été représentées, mais il n’y a aucun doute quant à leur orientation) :
Cette relation est transitive : si ![]() divise
divise ![]() et si
et si ![]() divise
divise ![]() alors il existe des entiers naturels
alors il existe des entiers naturels ![]() et
et ![]() tels que
tels que ![]() et
et ![]() d’où
d’où ![]() et donc
et donc ![]() divise
divise ![]()
Il n’est très pas difficile de dénombrer les relations binaires sur un ensemble ![]() de cardinal
de cardinal ![]() : il en existe
: il en existe ![]() (
(![]() à la puissance
à la puissance ![]() ). Disons, sans rentrer dans les détails, que ceci résulte de l’existence d’une bijection de l’ensemble des relations binaires sur
). Disons, sans rentrer dans les détails, que ceci résulte de l’existence d’une bijection de l’ensemble des relations binaires sur ![]() vers l’ensemble des applications de
vers l’ensemble des applications de ![]() dans
dans ![]() .
.
On en vient à la question qui tue …
Question : combien de relations binaires transitives peut-on définir sur un ensemble de cardinal ![]() ?
?
Réponse : un entier ![]() pour lequel aucune formule sympathique n’a été trouvée à ce jour…
pour lequel aucune formule sympathique n’a été trouvée à ce jour…
Tout au plus peut-on (avec l’aide d’un ordinateur) calculer la valeur de ![]() pour de petites valeurs de n, mais guère plus. Voici, compilés dans une table, les 10 premiers termes de cette suite de nombres :
pour de petites valeurs de n, mais guère plus. Voici, compilés dans une table, les 10 premiers termes de cette suite de nombres :
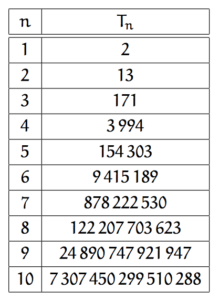
Un bon exercice consiste à dessiner (patates et flèches…) les graphes des ![]() relations binaires possibles sur un ensemble à deux éléments, puis de recenser celles d’entre-elles qui sont transitives (on en trouve
relations binaires possibles sur un ensemble à deux éléments, puis de recenser celles d’entre-elles qui sont transitives (on en trouve ![]() ).
).
4 – Ensembles infinis en bijection
Nous avons dit, au début de la section précédente, qu’étant donnés deux ensembles finis ![]() et
et ![]() , les conditions :
, les conditions :
- il existe une bijection de
 vers
vers 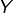
 et
et 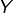 possèdent le même nombre d’éléments
possèdent le même nombre d’éléments
sont équivalentes. Mais pour des ensembles infinis (c’est-à-dire comportant une infinité d’éléments), l’expression « posséder le même nombre d’éléments » n’a plus grand sens…
D’ailleurs, les choses deviennent dans ce contexte nettement moins intuitive : dans certains cas, on observe l’existence de bijections entre deux ensembles pour lesquels on a bien l’impression que l’un est plus « gros » que l’autre… (par exemple parce qu’il le contient strictement).
Cela provient du fait que notre esprit élabore, en raison d’une terminologie inadaptée, une représentation incorrecte de la situation.
Lorsqu’il existe une bijection entre un ensemble E et l’ensemble ![]() des entiers naturels, l’ensemble E est dit dénombrable.
des entiers naturels, l’ensemble E est dit dénombrable.
Voici deux exemples très classiques, mais qui peuvent paraître contre-intuitifs au premier abord :
Dénombrabilité de 
Les entiers naturels 0, 1, 2, etc… forment un ensemble noté ![]()
Si l’on rajoute les entiers négatifs -1,-2, etc… on obtient un ensemble « plus gros » noté ![]() (initiale du mot allemand « Zahl » qui signifie nombre). Les éléments de
(initiale du mot allemand « Zahl » qui signifie nombre). Les éléments de ![]() sont les « entiers relatifs ».
sont les « entiers relatifs ».
Intuitivement, on a envie de dire « qu’il y a deux fois plus d’éléments dans ![]() que dans
que dans ![]() » ! Nous pourrions donc penser qu’il n’existe aucune bijection de
» ! Nous pourrions donc penser qu’il n’existe aucune bijection de ![]() vers
vers ![]()
Pourtant, c’est exactement le contraire qui se passe : on peut énumérer les entiers relatifs de manière à ce que chacun d’eux soit pris en compte et que l’on ne prenne jamais deux fois le même.
Pour cela, il est hors de question de commencer par les entiers positifs, en se disant que « dès qu’on en aura fini avec eux », on pourra passer aux négatifs… et pour cause : on n’aura jamais fini !
En revanche, on peut envisager une « énumération alternée » : un coup positif, un coup négatif, et on recommence…
Le diagramme ci-dessous permet de visualiser les premières étapes de cette énumération :
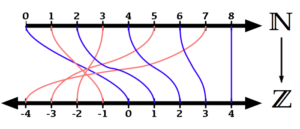
Plus formellement, à chaque entier naturel ![]() on associe un entier relatif noté
on associe un entier relatif noté ![]() défini par :
défini par :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$f\left(n\right)=\left\{ \begin{array}{cc}{\displaystyle \frac{n}{2}} & \text{si }n\text{ est pair}\\\\{\displaystyle -\frac{n+1}{2}} & \text{si }n\text{ est impair}\end{array}\right.$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7c96e3da1a13d94e2700a072c3157fd5_l3.png)
et il est facile de montrer que f est une bijection de ![]() vers
vers ![]()
Ainsi, l’ensemble ![]() des entiers relatifs est donc dénombrable.
des entiers relatifs est donc dénombrable.
Dénombrabilité de 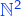
On peut montrer que l’ensemble noté ![]() des couples d’entiers naturels est aussi dénombrable. Une bijection naturelle de
des couples d’entiers naturels est aussi dénombrable. Une bijection naturelle de ![]() vers
vers ![]() est d’ailleurs suggérée par la figure suivante : on énumère les couples d’entiers naturels en partant de
est d’ailleurs suggérée par la figure suivante : on énumère les couples d’entiers naturels en partant de ![]() et en parcourant les “ diagonales ” successives, c’est-à-dire les ensembles
et en parcourant les “ diagonales ” successives, c’est-à-dire les ensembles ![]() pour
pour ![]()
Les ensembles ![]() ,
, ![]() ,
, ![]() , etc… sont deux à deux disjoints et leur union est
, etc… sont deux à deux disjoints et leur union est ![]() tout entier. Mais le point important, c’est que ces ensembles sont tous finis, ce qui garantit que, peu importe le couple
tout entier. Mais le point important, c’est que ces ensembles sont tous finis, ce qui garantit que, peu importe le couple ![]() considéré, on arrivera jusqu’à lui en un nombre fini d’étapes, après avoir parcouru un certain nombre de diagonales. On retrouve là, sous une forme plus élaborée, l’idée qui a permis plus haut de mettre
considéré, on arrivera jusqu’à lui en un nombre fini d’étapes, après avoir parcouru un certain nombre de diagonales. On retrouve là, sous une forme plus élaborée, l’idée qui a permis plus haut de mettre ![]() et
et ![]() en bijection.
en bijection.
Dans la figure ci-dessous, les points qui composent l’ensemble ![]() sont alignés sur le segment rouge :
sont alignés sur le segment rouge :
5 – Une bijection de  vers
vers 
Ce qui suit sera un peu technique et fera intervenir des connaissances généralement enseignées en première année de licence de maths ou de classe préparatoire scientifique.
Pour les besoins d’un explication ultérieure (la non-dénombrabilité de ![]() , cf. section 6), nous allons établir une bijection de
, cf. section 6), nous allons établir une bijection de ![]() vers
vers ![]()
Dans un premier temps, modifions légèrement l’objectif et construisons plutôt une bijection de ![]() vers
vers ![]() Le simple fait de supprimer l’extrémité gauche de l’intervalle
Le simple fait de supprimer l’extrémité gauche de l’intervalle ![]() va en effet nous faciliter les choses…
va en effet nous faciliter les choses…
Considérons l’application
![]()
Afin d’obtenir une bijection de ![]() vers
vers ![]() il suffit de construire une bijection
il suffit de construire une bijection ![]() de
de ![]() vers
vers ![]() et de considérer la composée de
et de considérer la composée de ![]() par
par ![]() (cf. section 2).
(cf. section 2).
Posons donc :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$v:\left]0,1\right[\rightarrow\left]0,1\right],\thinspace x\mapsto\left\{ \begin{array}{cc}2x & \text{si }x\in\left\{ 2^{-n};\thinspace n\in\mathbb{N}^{\star}\right\} \\\\x & \text{sinon}\end{array}\right.$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-203979639b42d1044bb26de12b852618_l3.png)
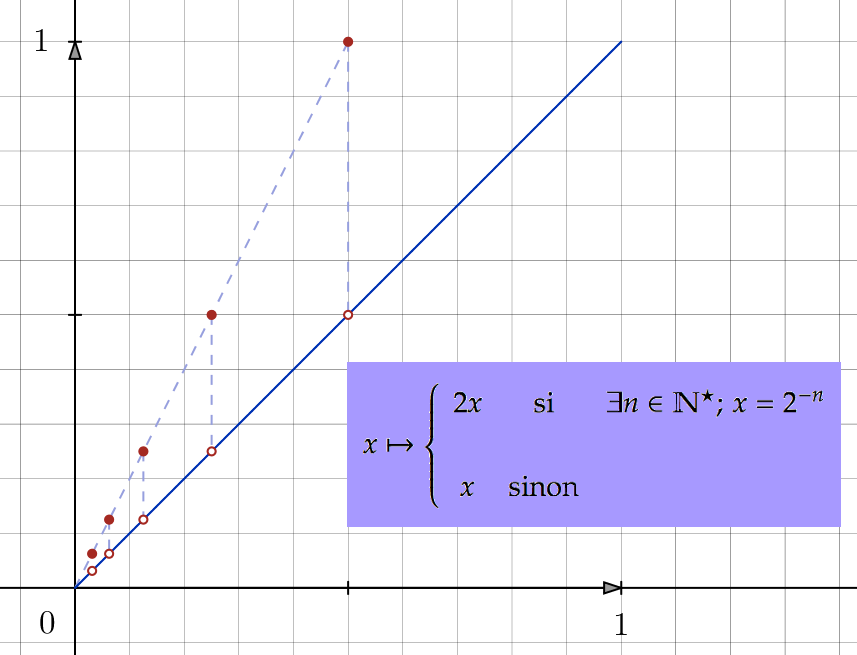
Enfin, l’application
![]()
Nous tenons notre bijection de ![]() vers
vers ![]() .
.
6 – La diagonale de Cantor
On doit au mathématicien allemand Georg Cantor (1845 – 1918) le résultat suivant :
Théorème
L’ensemble ![]() n’est pas dénombrable.
n’est pas dénombrable.
Comme nous disposons (cf. section 5) d’une bijection de ![]() vers
vers ![]() l’existence d’une bijection de
l’existence d’une bijection de ![]() vers
vers ![]() entraînerait (par composition) l’existence d’une bijection de
entraînerait (par composition) l’existence d’une bijection de ![]() vers
vers ![]() Il est donc suffisant de montrer qu’une telle bijection n’existe pas, ce qui se fait bien sûr par l’absurde.
Il est donc suffisant de montrer qu’une telle bijection n’existe pas, ce qui se fait bien sûr par l’absurde.
Tout nombre réel ![]() appartenant à l’intervalle
appartenant à l’intervalle ![]() peut s’écrire, de manière unique, sous la forme d’un développement décimal propre (en abrégé : DDP), c’est-à-dire quelque chose du style :
peut s’écrire, de manière unique, sous la forme d’un développement décimal propre (en abrégé : DDP), c’est-à-dire quelque chose du style :
![]()
Exemple : développement décimal de 1/2
Le nombre ![]() peut s’écrire, au choix :
peut s’écrire, au choix :
➡ 0,500000… avec une infinité de 0 après le 5, ce que tout le monde note simplement 0,5
➡ ou bien 0,499999… avec une infinité de 9 après le 4
Vous avez un doute ? Vous pensez que le second est légèrement inférieur au premier ?
Ok, détaillons …
De façon incontestable :
![]()

![]()
De ces deux écritures, on retiendra donc la première, qui constitue le DDP de ![]()
Supposons maintenant l’existence d’une bijection ![]() Pour chaque entier naturel
Pour chaque entier naturel ![]() le DDP de
le DDP de ![]() peut s’écrire :
peut s’écrire :
![]()
C’est là qu’intervient l’idée géniale ![]() de Cantor. Il considère un nombre réel
de Cantor. Il considère un nombre réel ![]() dont le DDP est
dont le DDP est
![]()
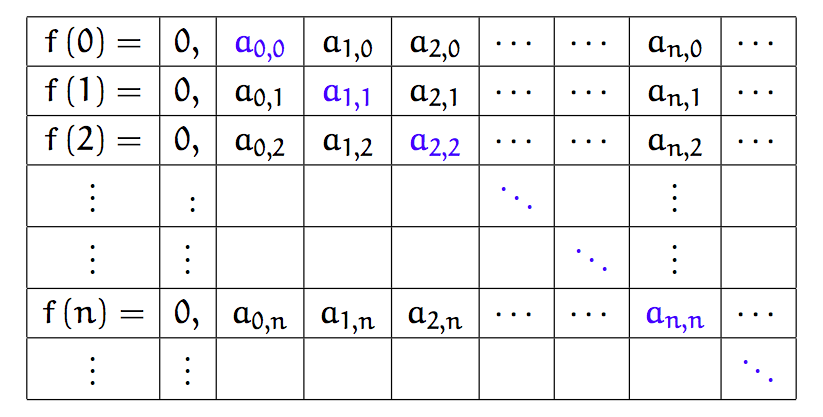
On peut imaginer un tableau comportant, ligne par ligne, les DDP de ![]() ,
, ![]() ,
, ![]() , etc…
, etc…
Ce tableau comporte donc une infinité de lignes et chaque ligne comporte une infinité de colonnes ! L’idée de Cantor consiste donc à choisir une séquence de chiffres ![]() ,
, ![]() ,
, ![]() de telle sorte que, pour tout
de telle sorte que, pour tout ![]() le chiffre
le chiffre ![]() soit distinct du n-ème terme de la diagonale.
soit distinct du n-ème terme de la diagonale.
Comme ![]() et vue l’unicité du DDP, il est certain que
et vue l’unicité du DDP, il est certain que ![]()
De même, comme ![]() et vue l’unicité du DDP, il est certain que
et vue l’unicité du DDP, il est certain que ![]()
L’argument se généralise : quel que soit l’entier naturel n, on est certain que ![]()
Ainsi, ![]() ne possède aucun antécédent par
ne possède aucun antécédent par ![]() , ce qui est absurde puisque
, ce qui est absurde puisque ![]() est supposée bijective !
est supposée bijective !
Vos questions ou remarques seront toujours les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.
