1 – Préambule et notations
Pour tout entier naturel ![]() on désigne par
on désigne par ![]() l’ensemble des entiers
l’ensemble des entiers ![]() vérifiant
vérifiant ![]() .
.
Noter que : ![]()
Définition
Un ensemble E est dit fini lorsqu’il existe un entier naturel ![]() et une bijection de
et une bijection de ![]() vers
vers ![]() . On peut montrer l’unicité d’un tel
. On peut montrer l’unicité d’un tel ![]() : c’est le cardinal de
: c’est le cardinal de ![]() , noté
, noté ![]() .
.
Intuitivement, ![]() indique le nombre d’éléments de
indique le nombre d’éléments de ![]() .
.
On peut démontrer (nous l’admettrons ici) la :
Proposition 1
Proposition 2
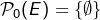
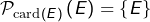
- si
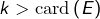 , alors
, alors 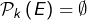
Nous aurons enfin à utiliser le :
Principe Additif
Si ![]() sont deux ensembles finis et disjoints, alors
sont deux ensembles finis et disjoints, alors ![]() est fini et :
est fini et :
![]()
![Rendered by QuickLaTeX.com \[\text{card}\left(\bigcup_{i=1}^{p}E_{i}\right)=\sum_{i=1}^{p}\text{card}\left(E_{i}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8882e097bdf0a3e2a697d77abd9c1a3f_l3.png)
2 – Point de vue combinatoire sur les coefficients binomiaux
Définition
![Rendered by QuickLaTeX.com \[\boxed{\binom{n}{k}=\text{card}\left(\mathcal{P}_{k}\left(\mathbb{N}_{n}\right)\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3df2860214b6571a85821332b466461b_l3.png)
Exemple
![]()
![]()
![]()
3 – Formule de symétrie
Ces ![]() éléments, qui sont mis de côté, sont donc – en un sens – « choisis » eux aussi !
éléments, qui sont mis de côté, sont donc – en un sens – « choisis » eux aussi !
Il n’est donc pas surprenant qu’on ait :
Proposition
Pour tout ![]() et pour tout
et pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\boxed{\binom{n}{k}=\binom{n}{n-k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1b3a7b54f3dda090086b23e889ba2261_l3.png)
C’est la formule de symétrie des coefficients binomiaux.
En voici une justification rigoureuse.
Preuve (cliquer pour déplier / replier)
Soit ![]() un ensemble de cardinal
un ensemble de cardinal ![]() . Pour chaque partie
. Pour chaque partie ![]() de
de ![]() , notons
, notons ![]() le complémentaire de
le complémentaire de ![]() dans
dans ![]() et considérons les applications :
et considérons les applications :
![]()
![]()
Comme le complémentaire du complémentaire d’une partie ![]() n’est autre que
n’est autre que ![]() , il est clair que :
, il est clair que :
![]()
Il s’ensuit que ![]() et
et ![]() sont des bijections (et que chacune est la réciproque de l’autre).
sont des bijections (et que chacune est la réciproque de l’autre).
En particulier, ![]() et
et ![]() sont équipotents, d’où la formule.
sont équipotents, d’où la formule.
4 – Formule de Pascal
Soient ![]() deux entiers naturels tels que
deux entiers naturels tels que ![]() et
et ![]() .
.
Considérons un ensemble ![]() de cardinal
de cardinal ![]() ainsi qu’un élément particulier de
ainsi qu’un élément particulier de ![]() , que nous notons
, que nous notons ![]() .
.
Les parties de ![]() de cardinal
de cardinal ![]() , qui sont au nombre de
, qui sont au nombre de ![]() , peuvent être classées en deux catégories :
, peuvent être classées en deux catégories :
- celles qui ne contiennent pas
 ,
, - celles qui contiennent
 .
.
Les premières sont les parties de cardinal ![]() de
de ![]() . Il en existe
. Il en existe ![]() .
.
Les autres s’obtiennent en ajoutant ![]() à une partie de cardinal
à une partie de cardinal ![]() de
de ![]() : il en existe donc autant que de parties de cardinal
: il en existe donc autant que de parties de cardinal ![]() de
de ![]() , c’est-à-dire
, c’est-à-dire ![]() .
.
Ce raisonnement prouve, via le principe additif, que :
Proposition
Pour tout ![]() et pour tout
et pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\boxed{\binom{n+1}{k+1}=\binom{n}{k+1}+\binom{n}{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1bfb5d8b44f22858a8748ef814291657_l3.png)
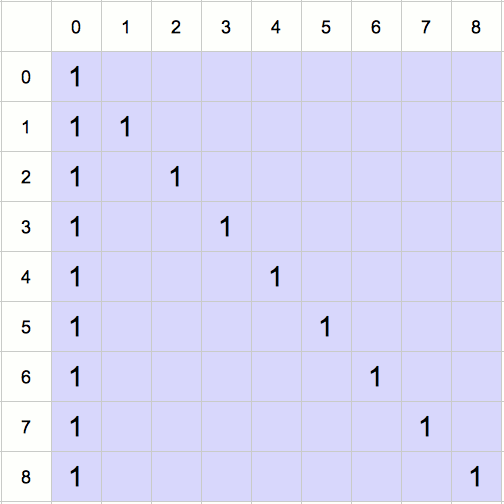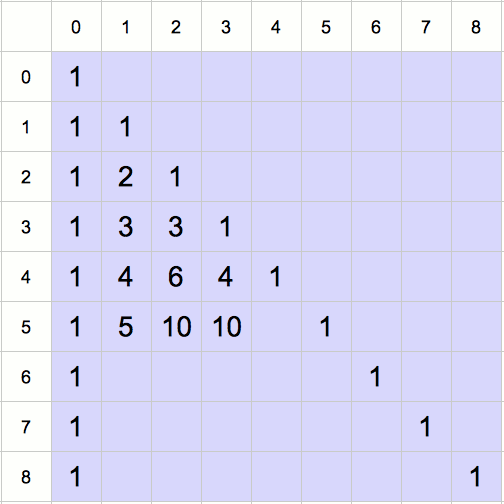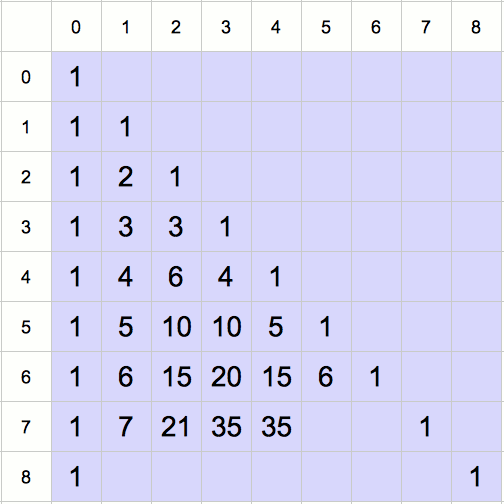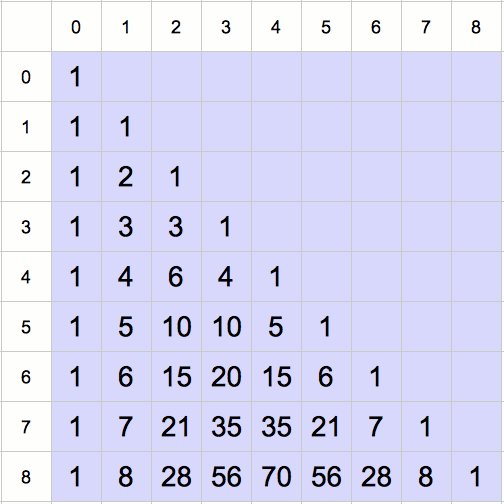
Cette relation (appelée formule de Pascal) permet de construire un tableau, appelé « triangle de Pascal », qui renferme les valeurs des coefficients binomiaux. La valeur de ![]() est placée à l’intersection de la ligne n et de la colonne k.
est placée à l’intersection de la ligne n et de la colonne k.
➣ Comme ![]() pour tout
pour tout ![]() , on place au préalable des ‘1’ sur la colonne 0 et sur la diagonale.
, on place au préalable des ‘1’ sur la colonne 0 et sur la diagonale.
➢ Ensuite, on utilise la formule encadrée pour « garnir » la table, ligne par ligne.
L’animation suivante montre le remplissage du triangle de Pascal, jusqu’à la ligne 8 :
5 – Formule de Fermat
Nous sommes maintenant en mesure d’établir une formule adaptée au calcul direct de ![]() .
.
Il s’agit de la « formule de Fermat » :
Proposition
Pour tout ![]() et pour tout
et pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\boxed{\binom{n}{k}=\frac{n!}{k!\left(n-k\right)!}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ab93fe5b31ec392e14d819912e33b401_l3.png)
Si la notion de factorielle vous est peu familière, je vous suggère la lecture des articles suivants :
- Qu’est-ce qu’une factorielle ? Partie 1 (article de vulgarisation)
- Qu’est-ce qu’une factorielle ? Partie 2 – (article de niveau supérieur)
La formule encadrée se prouve par récurrence sur ![]() . Pour
. Pour ![]() , il est clair que :
, il est clair que :
![]()
Supposons ensuite que, pour un certain ![]() , on ait pour tout
, on ait pour tout ![]() :
:
![]()
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\binom{n+1}{k} & = \binom{n}{k}+\binom{n}{k-1}\\& = \frac{n!}{k!\left(n-k\right)!}+\frac{n!}{\left(k-1\right)!\left(n-k+1\right)!}\\& = \frac{n!}{\left(k-1\right)!\left(n-k\right)!}\left[\frac{1}{k}+\frac{1}{n-k+1}\right]\\& = \frac{n!}{\left(k-1\right)!\left(n-k\right)!}\:\frac{n+1}{k\left(n-k+1\right)}\end{split}\end{equation*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-4ec86cbe294ed2a6e002ab34be7a97db_l3.png)
![]()
Cette égalité est encore vraie pour ![]() et pour
et pour ![]() , et la formule de Fermat est donc établie.
, et la formule de Fermat est donc établie.
Pour les calculs numériques, il est pratique d’utiliser ceci :
Version simplifiée de la formule de Fermat
Pour tout ![]() et pour tout
et pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\boxed{\binom{n}{k}=\frac{n\left(n-1\right)\cdots\left(n-k+1\right)}{k!}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-942c1cf51b0a2324c4a9a50045436201_l3.png)
On retiendra que le numérateur et le dénominateur de cette fraction sont chacun le produit de ![]() entiers consécutifs. Ceci peut aider à mémoriser correctement la formule.
entiers consécutifs. Ceci peut aider à mémoriser correctement la formule.
Quelques Exemples
Exemple 1
De combien de façons peut-on choisir 6 cartes à jouer dans un paquet de 16 cartes ?
Réponse :
![]()
Exemple 2
Une grille de loto comporte 49 numéros.
De combien de façons le joueur peut-il en choisir 6 ?

Réponse :
![]()
Remarquons, pour conclure cette section, que la formule de Fermat exprime une propriété arithmétique intéressante en soi, à savoir qu’étant donné un entier ![]() , tout produit de
, tout produit de ![]() entiers consécutifs est multiple de la factorielle de
entiers consécutifs est multiple de la factorielle de ![]() . En effet, étant donné
. En effet, étant donné ![]() :
:
![]()
Pour plus de détails à ce sujet, je vous invite à lire l’article (n+1)(n+2)…(n+k) est multiple de k!
6 – Formule du binôme de Newton
Au collège, on apprend l’identité remarquable ![]() .
.
La formule du binôme en donne une version généralisée, avec un exposant quelconque :
Proposition
Pour tout ![]() et pour tout
et pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\boxed{\left(a+b\right)^{n}=\sum_{k=0}^{n}\binom{n}{k}a^{k}b^{n-k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c2f25929e91a4a923f7596e76003654b_l3.png)
Commençons par en donner une preuve combinatoire.
En développant « brutalement » l’expression ![]() , on obtient
, on obtient ![]() termes, qui sont tous de la forme
termes, qui sont tous de la forme ![]() pour un certain
pour un certain ![]() .
.
Pour une valeur donnée de ![]() , combien de fois le terme
, combien de fois le terme ![]() apparaît-il ? C’est simple : il suffit de voir que, pour obtenir ce terme, on doit sélectionner la lettre
apparaît-il ? C’est simple : il suffit de voir que, pour obtenir ce terme, on doit sélectionner la lettre ![]() dans
dans ![]() facteurs et la lettre
facteurs et la lettre ![]() dans les
dans les ![]() autres, ce qui peut se faire de
autres, ce qui peut se faire de ![]() façons.
façons.
Pour chaque ![]() , le terme
, le terme ![]() apparaît donc
apparaît donc ![]() fois dans le développement de
fois dans le développement de ![]() . La formule du binôme en résulte.
. La formule du binôme en résulte.
On peut aussi envisager une …
Preuve par récurrence (cliquer pour déplier / replier)
Etant donnés ![]() , on considère l’assertion :
, on considère l’assertion :
![Rendered by QuickLaTeX.com \[\left(\mathcal{A}_{n}\right)\::\qquad\qquad\left(a+b\right)^{n}=\sum_{k=0}^{n}\binom{n}{k}a^{k}b^{n-k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7a0c9340df7c267c0ae73ad3ab79cf30_l3.png)
![]()
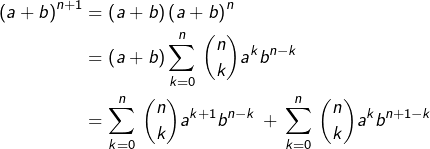
Si l’on effectue dans la première somme le changement d’indice ![]() , il vient :
, il vient :
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\left(a+b\right)^{n+1} & = \sum_{j=1}^{n+1}\,\binom{n}{j-1}a^{j}b^{n+1-j}+\sum_{j=0}^{n}\,\binom{n}{j}a^{j}b^{n+1-j}\\& = a^{n+1}+b^{n+1}+\sum_{j=1}^{n}\,\left[\binom{n}{j-1}+\binom{n}{j}\right]a^{j}b^{n+1-j}\\& = a^{n+1}+b^{n+1}+\sum_{j=1}^{n}\binom{n+1}{j}a^{j}b^{n+1-j}\\& = \sum_{j=0}^{n+1}\,\binom{n+1}{j}a^{j}b^{n+1-j}\end{split}\end{equation*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-75c8b92641ffb345011ebfc0abdd51f4_l3.png)
L’avant-dernière égalité résulte de la formule de Pascal. La dernière s’obtient en ré-insérant les termes ![]() et
et ![]() dans le
dans le ![]() (ils correspondent respectivement à
(ils correspondent respectivement à ![]() et à
et à ![]() ).
).
L’assertion ![]() est donc établie, ce qui achève la démonstration.
est donc établie, ce qui achève la démonstration.
7 – Formule du pion
Proposition
![Rendered by QuickLaTeX.com \[\boxed{k\binom{n}{k}=n\binom{n-1}{k-1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6522b65914c85b49380b011f2feb80ad_l3.png)
Cette appellation est sans doute due à une vague analogie avec le jeu d’échec : lorsqu’un pion attaque un pion adverse, il se déplace d’une case en diagonale (disons depuis la case située à l’intersection de la ligne ![]() et de la colonne
et de la colonne ![]() vers celle située à l’intersection de la ligne
vers celle située à l’intersection de la ligne ![]() et de la colonne
et de la colonne ![]() ), comme l’indique le schéma ci-dessous :
), comme l’indique le schéma ci-dessous :
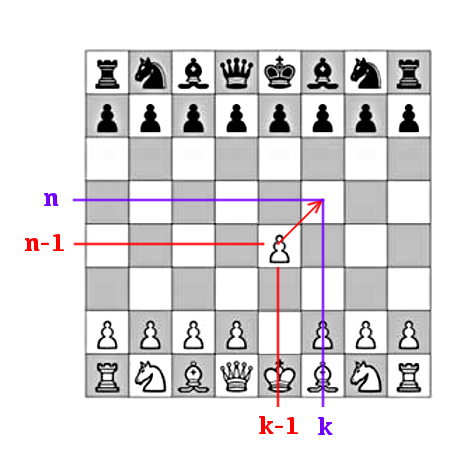
Cette formule peut être établie de deux manières : par un calcul ou bien par un raisonnement combinatoire.
Preuve 1 – par calcul (cliquer pour déplier / replier)
Avec la formule de Fermat, on voit facilement que :
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}k\binom{n}{k} & = k\:\frac{n!}{k!\left(n-k\right)}\\& = \frac{n\left(n-1\right)!}{\left(k-1\right)!\left[\left(n-1\right)-\left(k-1\right)\right]!}\\& = n\binom{n-1}{k-1}\end{split}\end{equation*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-02d8bb8cdcfcf6d3e4831fc1ab20a9da_l3.png)
Mais le point de vue combinatoire est clairement plus instructif …
Preuve 2 – combinatoire (cliquer pour déplier / replier)
Etant donné un ensemble ![]() de cardinal
de cardinal ![]() et un entier
et un entier ![]() tel que
tel que ![]() , on va dénombrer les couples
, on va dénombrer les couples ![]() tels que :
tels que :
![]()
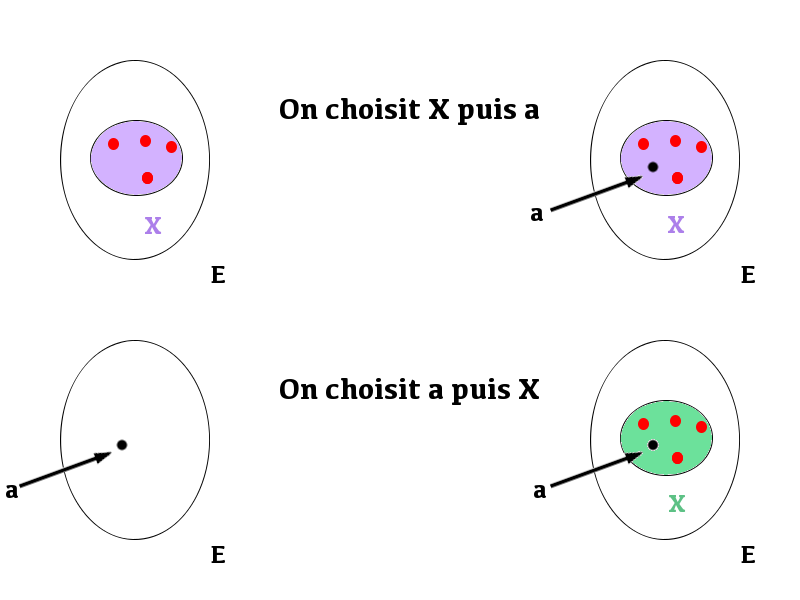
Pour cela, on peut choisir d’abord ![]() de
de ![]() façons, puis choisir
façons, puis choisir ![]() de
de ![]() façons : au total, on trouve
façons : au total, on trouve ![]() couples.
couples.
Une autre méthode consiste à choisir d’abord ![]() de
de ![]() façons, puis à « l’entourer » de
façons, puis à « l’entourer » de ![]() éléments choisis dans
éléments choisis dans ![]() , et ce de
, et ce de ![]() façons : au total, on trouve
façons : au total, on trouve ![]() couples.
couples.
La formule du pion en résulte.
Vous en trouverez un exemple d’utilisation dans la vidéo Calcul de sommes – 01.
L’illustration ci-dessous permet de visualiser les deux manières de compter :
8 – Formule de Vandermonde
Considérons un ensemble ![]() de cardinal
de cardinal ![]() . Le nombre de parties de
. Le nombre de parties de ![]() qui sont de cardinal
qui sont de cardinal ![]() est, par définition
est, par définition ![]() . Mais on peut raisonner autrement.
. Mais on peut raisonner autrement.
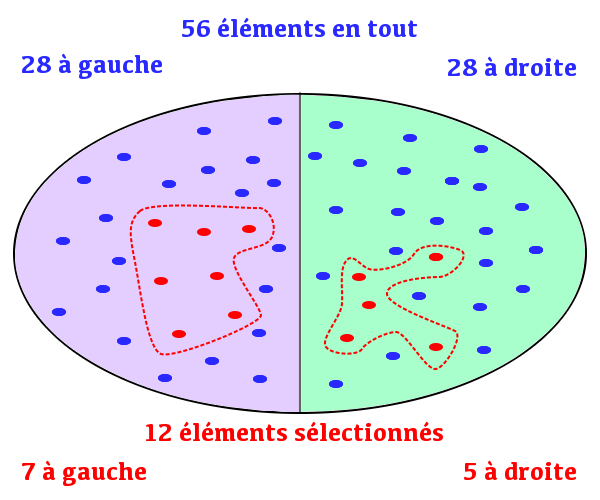
On commence par fixer deux parties complémentaires et de même cardinal ![]() (autrement dit : on place une « cloison » dans
(autrement dit : on place une « cloison » dans ![]() ). Se donner une partie de
). Se donner une partie de ![]() de cardinal
de cardinal ![]() revient alors à choisir, pour un certain
revient alors à choisir, pour un certain ![]() ,
, ![]() éléments d’un côté de la cloison et
éléments d’un côté de la cloison et ![]() éléments de l’autre. La figure ci-dessous montre l’une des
éléments de l’autre. La figure ci-dessous montre l’une des ![]() manières de choisir 12 objets parmi 56 :
manières de choisir 12 objets parmi 56 :
Pour ![]() donné, le nombre de ces double-choix est
donné, le nombre de ces double-choix est ![]() , c’est-à-dire
, c’est-à-dire ![]() .
.
Ces possibilités s’excluent mutuellement, ce qui autorise l’usage du principe additif mentionné en début d’article. En ajoutant, il vient :
![Rendered by QuickLaTeX.com \[q_{n}=\sum_{k=0}^{n}\binom{n}{k}^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-34d95afd7c18973102e6335d08e98176_l3.png)
Par conséquent :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N},\thinspace\sum_{k=0}^{n}\binom{n}{k}^{2}=\binom{2n}{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-024fec1ff5ebcdb43703139c2c8ecdf7_l3.png)
On peut aisément généraliser : pour dénombrer les parties d’un ensemble ![]() de cardinal
de cardinal ![]() qui sont de cardinal
qui sont de cardinal ![]() (avec
(avec ![]() ). On cloisonne
). On cloisonne ![]() en deux parties de cardinaux respectifs
en deux parties de cardinaux respectifs ![]() et
et ![]() puis, en raisonnant comme ci-dessus, on parvient à la formule de Vandermonde :
puis, en raisonnant comme ci-dessus, on parvient à la formule de Vandermonde :
![Rendered by QuickLaTeX.com \[\boxed{\forall\left(a,b\right)\in\mathbb{N}^{2},\:\forall n\in\llbracket0,a+b\rrbracket,\thinspace\sum_{k=\max\left{ 0,n-b\right} }^{\min\left{ a,n\right} }\binom{a}{k}\binom{b}{n-k}=\binom{a+b}{n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2343514aa9e628dea2ea5be573cd85fa_l3.png)
Si l’on convient que ![]() dès que
dès que ![]() ou
ou ![]() , cette formule s’écrit plus simplement :
, cette formule s’écrit plus simplement :
Proposition
Pour tout ![]() et pour tout
et pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=0}^{n}\binom{a}{k}\binom{b}{n-k}=\binom{a+b}{n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3241426d3aacfa494fb8992d4472b870_l3.png)
En voici une illustration «concrète». Etant donné un jeu de 32 cartes, on peut compter le nombre de «mains» (une main est un ensemble de 5 cartes extraites du jeu) : il en existe évidemment ![]() . Si l’on note
. Si l’on note ![]() le nombre de mains comportant exactement
le nombre de mains comportant exactement ![]() rois (pour
rois (pour ![]() ), on voit que :
), on voit que :
![]()
![]()
![]()
![]()
9 – Somme d’une colonne dans le triangle de Pascal
Reprenons le triangle de Pascal et examinons ce qui se passe lorsqu’on ajoute les termes d’une colonne, depuis le terme diagonal (qui vaut 1) jusqu’à une certaine profondeur.
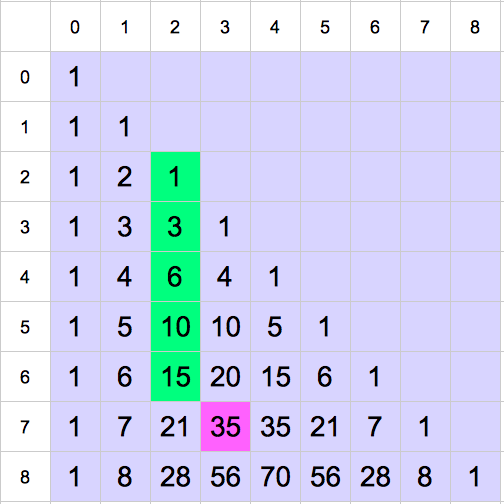
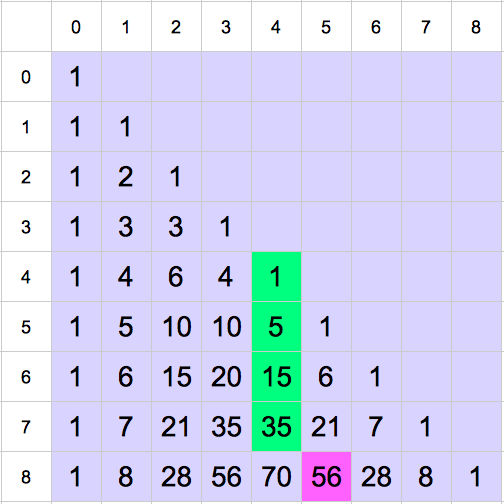
Après quelques essais, on conjecture qu’une telle somme est égale au coefficient binomial situé « en-dessous, à droite » de la colonne considérée. Plus formellement :
Proposition
Pour tout ![]() et pour tout
et pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=p}^{n}\binom{k}{p}=\binom{n+1}{p+1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c25feb297177250dc93bae964d0aae3e_l3.png)
Cette relation est prouvable grâce à une sommation télescopique (pour savoir ce qu’est une « sommation télescopique », voir l’article : Manipulation de sommes à l’aide du symbole ∑)
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\sum_{k=p}^{n}\binom{k}{p} & = 1+\sum_{k=p+1}^{n}\binom{k}{p}\\\\& = 1+\sum_{k=p+1}^{n}\left[\binom{k+1}{p+1}-\binom{k}{p+1}\right]\\\\& = 1+\binom{n+1}{p+1}-\binom{p+1}{p+1}\\\\& = \binom{n+1}{p+1}\end{split}\end{equation*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-9949457a6c68b05dec3af97e6c7c6c53_l3.png)
Là encore, il est intéressant d’interpréter le résultat de manière combinatoire.
Détail de la preuve combinatoire (cliquer pour déplier / replier)
Ce point de vue est celui proposé par GD (voir plus bas dans les commentaires)
Notons ![]() la partie de
la partie de ![]() constituée des parties de
constituée des parties de ![]() de cardinal
de cardinal ![]() et dont le plus grand élément est
et dont le plus grand élément est ![]() , de sorte que
, de sorte que
![Rendered by QuickLaTeX.com \[{\mathcal P}_{p+1}\left(\llbracket1,n+1\rrbracket\right)=\bigcup_{k=p}^{n}E_{k+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2e026ca813fef7cea2af01fc67e450e1_l3.png)
![Rendered by QuickLaTeX.com \[\text{card}\left({\mathcal P}_{p+1}\left(\llbracket1,n+1\rrbracket\right)\right)=\sum_{k=p}^{n}\text{card}\left(E_{k+1}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-86c71fcdcbcb725c1acec8aaa8e0c662_l3.png)
Or, pour chaque ![]() , les éléments de
, les éléments de ![]() sont les
sont les
![]()
![]()
On retrouve ainsi la formule :
![Rendered by QuickLaTeX.com \[\binom{n+1}{p+1}=\sum_{k=p}^{n}\binom{k}{p}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-80ca56f8c5f04cb9b894e589c67a744f_l3.png)
10 – Coefficients binomiaux et nombres de Fibonacci
Reprenons le triangle de Pascal et ajoutons cette fois les termes d’une diagonale ascendante, comme indiqué sur la figure ci-dessous :
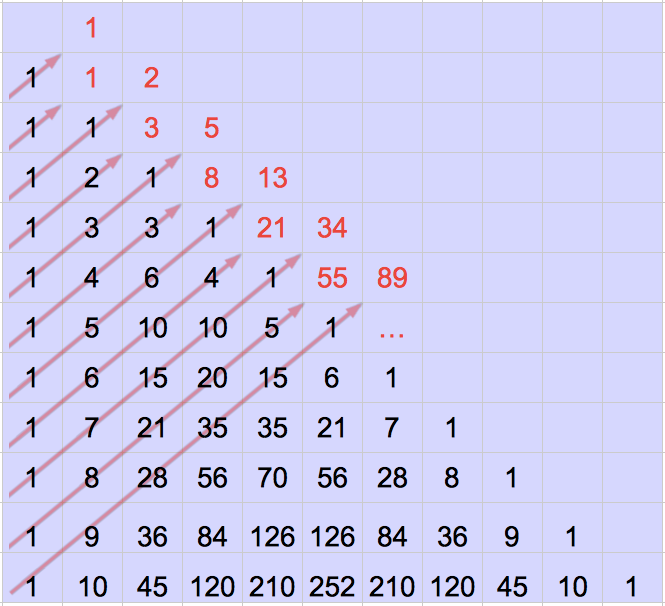
On voit apparaître une suite, qui commence par : 1, 1, 2, 3, 5, 8, 13, 21, 55, 89, 144, …
Vous aurez probablement reconnu les premiers termes de la célèbre suite de Fibonacci. Rappelons que cette suite est définie par :
![]()
Cette observation nous amène formuler la :
Proposition
Pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\sum_{k=0}^{\left\lfloor \frac{n}{2}\right\rfloor }\binom{n-k}{k}=F_{n+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e8536b2cf3245e21cc715d47a1abdf30_l3.png)
Preuve par récurrence (cliquer pour déplier / replier)
L’égalité se vérifie sans peine pour ![]() . Supposons-la vraie pour aux rangs
. Supposons-la vraie pour aux rangs ![]() et
et ![]() , pour un certain entier
, pour un certain entier ![]() et montrons qu’alors :
et montrons qu’alors :
![Rendered by QuickLaTeX.com \[\sum_{k=0}^{\left\lfloor \frac{n+1}{2}\right\rfloor }\binom{n+1-k}{k}=F_{n+2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-aee5b639dcaf8a04ff3703a682952663_l3.png)
Pour cela, distinguons deux cas, selon la parité de ![]() .
.
➣ Si ![]() est pair, on voit en posant
est pair, on voit en posant ![]() et en invoquant pour commencer la formule de Pascal, que :
et en invoquant pour commencer la formule de Pascal, que :
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\sum_{k=0}^{p+1}\binom{2p+2-k}{k} & = \binom{2p+2}{0}+\sum_{k=1}^{p}\left[\binom{2p+1-k}{k}+\binom{2p+1-k}{k-1}\right]+\binom{p+1}{p+1}\\\\& = \left[1+\sum_{k=1}^{p}\binom{2p+1-k}{k}\right]+\left[1+\sum_{j=0}^{p-1}\binom{2p-j}{j}\right]\end{split}\end{equation*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-ffda16b8d155933257e6c8bde77a7877_l3.png)
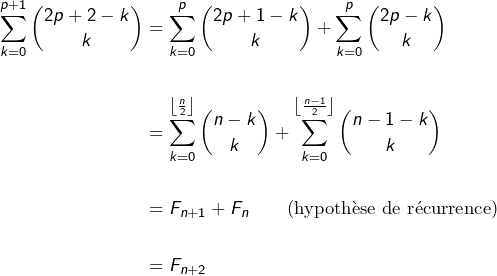
➣ Si ![]() est impair, on pose cette fois
est impair, on pose cette fois ![]() et le calcul est similaire :
et le calcul est similaire :
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\sum_{k=0}^{p}\binom{2p+1-k}{k} & = 1+\sum_{k=1}^{p}\left[\binom{2p-k}{k}+\binom{2p-k}{k-1}\right]\\\\& = \left[1+\sum_{k=1}^{p}\binom{2p-k}{k}\right]+\sum_{j=0}^{p-1}\binom{2p-1-j}{j}\\\\& = \sum_{k=0}^{p}\binom{2p-k}{k}+\sum_{k=0}^{p-1}\binom{2p-1-k}{k}\\\\& = \sum_{k=0}^{\left\lfloor \frac{n}{2}\right\rfloor }\binom{n-k}{k}+\sum_{k=0}^{\left\lfloor \frac{n-1}{2}\right\rfloor }\binom{n-1-k}{k}\\\\& = F_{n+1}+F_{n}\\\\& = F_{n+2}\end{split}\end{equation*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-5829993a081d96758f88514a1c4a72d7_l3.png)
Preuve combinatoire (cliquer pour déplier / replier)
Imaginons un petite grenouille, confortablement installée au pied d’un escalier. Elle doit le gravir, mais en respectant une consigne : elle ne peut effectuer que des sauts dirigés vers le haut de l’escalier et ne peut franchir qu’une marche ou deux à chaque saut.

De combien de façons la grenouille peut-elle gravir l’escalier ? Notons ![]() la réponse, qui dépend bien sûr du nombre
la réponse, qui dépend bien sûr du nombre ![]() de marches …
de marches …
On calcule facilement ![]() « à la main » pour les petites valeurs de
« à la main » pour les petites valeurs de ![]() :
:
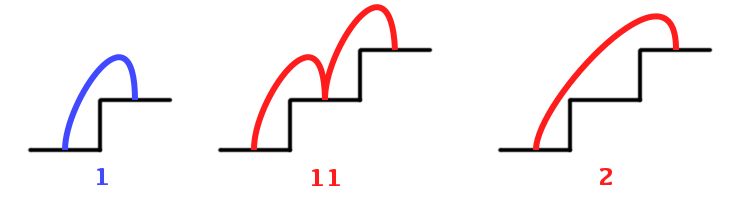
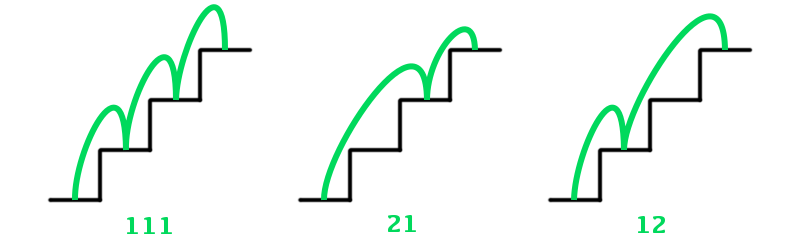
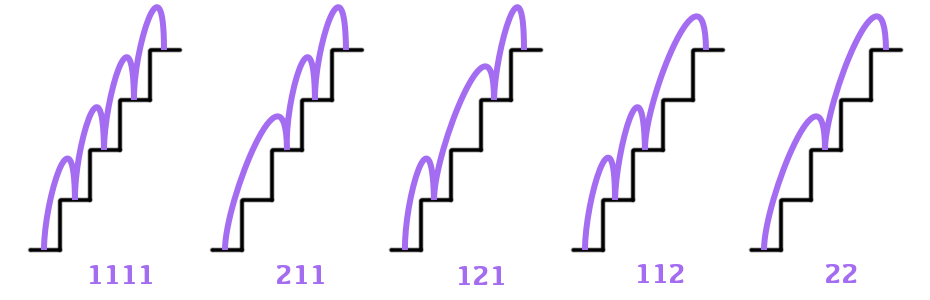
Ces quelques observations suggèrent la formule générale :
![]()
Celle-ci se prouve à l’aide d’une récurrence d’ordre 2.
Manifestement : ![]() ,
, ![]() . Supposons (hypothèse de récurrence) que
. Supposons (hypothèse de récurrence) que ![]() et
et ![]() .
.
Etant donné un escalier de ![]() marches (avec
marches (avec ![]() ), il existe
), il existe ![]() manières de le gravir en terminant par un saut de deux marches, et il en existe
manières de le gravir en terminant par un saut de deux marches, et il en existe ![]() autres se terminant par le franchissement d’une seule marche. Au total :
autres se terminant par le franchissement d’une seule marche. Au total : ![]() , comme souhaité.
, comme souhaité.
Changeons maintenant de point de vue pour le calcul de ![]() . Etant donné un entier naturel
. Etant donné un entier naturel ![]() , considérons le nombre de façons de gravir un escalier de
, considérons le nombre de façons de gravir un escalier de ![]() marches, en effectuant exactement
marches, en effectuant exactement ![]() sauts de deux marches (ce qui impose
sauts de deux marches (ce qui impose ![]() ).
).
Le nombre total de sauts effectués est alors : ![]() . Une telle façon de gravir l’escalier s’identifie à un mot de
. Une telle façon de gravir l’escalier s’identifie à un mot de ![]() lettres, chaque lettre pouvant être ‘1’ ou ‘2’ et le mot comportant un total de
lettres, chaque lettre pouvant être ‘1’ ou ‘2’ et le mot comportant un total de ![]() lettres ‘2’ : il existe
lettres ‘2’ : il existe ![]() tels mots. Le nombre de façons de gravir l’escalier est donc :
tels mots. Le nombre de façons de gravir l’escalier est donc :
![Rendered by QuickLaTeX.com \[\boxed{\forall n\in\mathbb{N}^{\star},\,u_{n}=\sum_{k=0}^{\left\lfloor \frac{n}{2}\right\rfloor }\,\binom{n-k}{k}}\qquad\left(\clubsuit\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-11a37ce4de763cd8729468e1b5409c66_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=0}^{\left\lfloor \frac{n}{2}\right\rfloor }\,\binom{n-k}{k}=F_{n+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-af9e234f804cb50aec9876c442b9ca73_l3.png)
J’espère que cet article vous sera utile !
Vous pouvez commencer à chercher des exercices relatifs aux coefficients binomiaux. Je vous ai préparé des énoncés ici.
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.


Une petite remarque : dans la démonstration de 9, il est inutile de faire intervenir les applications strictement croissantes.
Il suffit de dénombrer directement le nombre des parties à n+1 éléments d’un ensemble à p+1 éléments, soit n+1 parmi p+1
Puis on distingue selon la valeur du plus grand élément d’une telle partie, qui est nécessairement compris entre n+1 et p+1.
Si ce plus grand élément est k+1 avec n ≤ k ≤ p, on détermine une telle partie par ses n autres éléments dans [1, k].
Et il y a n parmi k telles façons de le faire.
La formule 9 en résulte aussitôt.
Bonjour et merci pour ce commentaire. En effet, ce point de vue est plus simple et donc plus éclairant. Je vais le signaler dans le corps du texte.
Dans l’argument plus rigoureux pour la symétrie des coefficients binomiaux, n’a t’on pas plutôt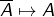 lorsqu’on écrit l’application
lorsqu’on écrit l’application 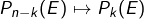 ?
?
Bonjour Joseph,
Le formalisme adopté dans l’article est le bon. D’une manière générale, lorsqu’on définit une application u de manière explicite, on spécifie son ensemble de départ E et son ensemble d’arrivée F ainsi que le “mécanisme” par lequel on associe, à chaque élément de E, son image par u. Un élément générique de E est généralement désigné par une lettre (x, y, …), à la rigueur par un couple ou plus généralement un n-uplet si E est un produit cartésien de deux ou plusieurs ensembles, mais JAMAIS par une expression plus complexe.
Par exemple, il est ILLICITE de définir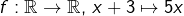 .
.
Dans l’exemple qui nous intéresse, on définit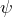 en disant qu’à chaque partie de E de cardinal n-k, on associe son complémentaire dans E. Cela dit, il est certain que si une partie de E de cardinal n-k se présente sous la forme du complémentaire d’un certain B, alors son image par
en disant qu’à chaque partie de E de cardinal n-k, on associe son complémentaire dans E. Cela dit, il est certain que si une partie de E de cardinal n-k se présente sous la forme du complémentaire d’un certain B, alors son image par 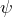 est B.
est B.