
Voici deux formules célèbres :
Formule du binôme de Newton
Pour tout entier naturel ![]() et tout couple
et tout couple ![]() de nombres réels :
de nombres réels :
(![]() )
) ![Rendered by QuickLaTeX.com \[\left(a+b\right)^{n}=\sum_{k=0}^{n}\binom{n}{k}a^{k}b^{n-k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-01d8dde42010981b0f6434ea83a3ed7f_l3.png)
Formule de Leibniz
Soit ![]() un intervalle de
un intervalle de ![]() (ni vide ni réduit à un singleton).
(ni vide ni réduit à un singleton).
Pour tout entier naturel ![]() et tout couple
et tout couple ![]() de fonctions indéfiniment dérivables sur
de fonctions indéfiniment dérivables sur ![]() :
:
(![]() )
) ![Rendered by QuickLaTeX.com \[\left(fg\right)^{\left(n\right)}=\sum_{k=0}^{n}\binom{n}{k}f^{\left(k\right)}g^{\left(n-k\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ddacdc907e90a5a141fe128842f593f5_l3.png)
Si ![]() est
est ![]() fois dérivable, sa dérivée
fois dérivable, sa dérivée ![]() ème est notée
ème est notée ![]() Les parenthèses autour de l’exposant permettent d’éviter toute confusion avec une puissance ordinaire (produit de
Les parenthèses autour de l’exposant permettent d’éviter toute confusion avec une puissance ordinaire (produit de ![]() fonctions égales à
fonctions égales à ![]() ou avec une itérée (composée de
ou avec une itérée (composée de ![]() par elle-même,
par elle-même, ![]() fois).
fois).
La ressemblance formelle entre les formules ![]() et
et ![]() est assez frappante !
est assez frappante !
- Comment expliquer cela ?
- Peut-on déduire chacune d’elles à partir de l’autre ?
- Ces deux formules peuvent-elles être vues comme des cas particuliers d’un résultat plus général ?
Telles sont les questions que je vous propose d’aborder dans cet article.
Une version abrégée de cette question est aussi consultable sur HighKholle
1 – Preuve classique de 
La formule du binôme se démontre généralement par récurrence.
On trouvera par ici une preuve détaillée, que je vous suggère vivement d’étudier avant de poursuivre la lecture de cet article.
Mais on aura besoin, dans la suite, d’une version plus générale de ce résultat :
Formule du binôme dans un anneau
Soit ![]() un anneau et soit
un anneau et soit ![]() un couple d’éléments de
un couple d’éléments de ![]() vérifiant
vérifiant ![]()
On dit que ![]() et
et ![]() commutent.
commutent.
Alors, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\left(a+b\right)^{n}=\sum_{k=0}^{n}\binom{n}{k}a^{k}b^{n-k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-96efa5408ea34faae09d7053a97a21d4_l3.png)
Rappelons à toutes fins utiles que, par définition d’un anneau :
- l’opération
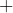 est commutative, associative et possède un élément neutre (qu’on peut noter
est commutative, associative et possède un élément neutre (qu’on peut noter 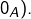 En outre, tout
En outre, tout 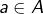 possède un symétrique pour l’opération
possède un symétrique pour l’opération 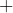 (c’est l’opposé de
(c’est l’opposé de 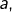 noté
noté 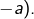
- l’opération
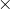 est associative et possède un élément neutre (qu’on peut noter
est associative et possède un élément neutre (qu’on peut noter 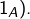 De plus, l’opération
De plus, l’opération  est distributive à gauche et à droite sur l’opération
est distributive à gauche et à droite sur l’opération 
Enfin, si ![]() et
et ![]() alors
alors ![]() désigne, par définition :
désigne, par définition :
![]()
![]()
![]()
La démonstration de cette version plus générale se fait par récurrence, tout comme dans le champ réel… mais sauriez-vous expliquer précisément où intervient l’hypothèse de commutation ?
2 – Preuve classique de 
Nous démontrons dans cette section la formule de Leibniz, en procédant par récurrence.
Un intervalle ![]() non trivial est fixé une fois pour toutes.
non trivial est fixé une fois pour toutes.
On considère, pour tout ![]() l’assertion suivante :
l’assertion suivante :
Assertion 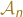
Pour tout couple ![]() d’applications indéfiniment dérivable sur
d’applications indéfiniment dérivable sur ![]() :
:
![Rendered by QuickLaTeX.com \[ \left(fg\right)^{\left(n\right)}=\sum_{k=0}^{n}\binom{n}{k}f^{\left(k\right)}g^{\left(n-k\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-20c8e339c3cd4a2693a8f1e7b3cbfaff_l3.png)
➣ L’assertion ![]() est évidemment vraie, puisque
est évidemment vraie, puisque ![]() : on ne dérive pas, tout simplement.
: on ne dérive pas, tout simplement.
➣ Supposons ![]() vraie pour un certain
vraie pour un certain ![]() et considérons un couple
et considérons un couple ![]() d’applications indéfiniment dérivables sur
d’applications indéfiniment dérivables sur ![]() En dérivant une fois la formule au rang
En dérivant une fois la formule au rang ![]() on obtient, par linéarité de la dérivation :
on obtient, par linéarité de la dérivation :
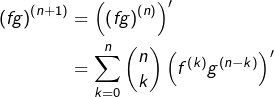
![Rendered by QuickLaTeX.com \[\left(fg\right)^{\left(n+1\right)}=\sum_{k=0}^{n}\binom{n}{k}\left(f^{\left(k+1\right)}g^{\left(n-k\right)}+f^{\left(k\right)}g^{\left(n+1-k\right)}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d2175fbc7cc1c09ace0e9494299bf883_l3.png)
![Rendered by QuickLaTeX.com \[\left(fg\right)^{\left(n+1\right)} =\sum_{k=1}^{n+1}\binom{n}{k-1}f^{\left(k\right)}g^{\left(n+1-k\right)}+\sum_{k=0}^{n}\binom{n}{k}f^{\left(k\right)}g^{\left(n+1-k\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e72c349689c9ba1fd82a4938c55bb014_l3.png)
![Rendered by QuickLaTeX.com \[\left(fg\right)^{\left(n+1\right)}=f^{\left(n+1\right)}g+fg^{\left(n+1\right)}+\sum_{k=1}^{n}\left[\binom{n}{k-1}+\binom{n}{k}\right]f^{\left(k\right)}g^{\left(n+1-k\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8cef4e0bd1985bf234e0aaada9579f24_l3.png)
![]()
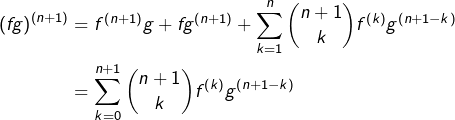
Remarque 1
Si vous avez en tête la preuve par récurrence de la formule du binôme, vous devez bien sentir qu’on a essentiellement refait la même chose… d’où l’idée de chercher une connexion entre les deux résultats : c’est ce qui motive le présent article.
Remarque 2
Il existe une meilleure version de la formule de Leibniz, dans laquelle les fonctions ![]() et
et ![]() sont supposées seulement
sont supposées seulement ![]() fois dérivables. J’ai choisi de me limiter au cas où
fois dérivables. J’ai choisi de me limiter au cas où ![]() et
et ![]() sont indéfiniment dérivables, afin de simplifier la présentation.
sont indéfiniment dérivables, afin de simplifier la présentation.
3 – Déduire  de
de  : astucieux mais simple
: astucieux mais simple
Considérons deux réels ![]() ainsi que les applications
ainsi que les applications ![]() définies par :
définies par :
![]()
![]()
![]()
Supposons connue la formule de Leibniz et appliquons-la à ce couple ![]() Il vient, pour tout
Il vient, pour tout ![]() et pour tout
et pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\left(a+b\right)^{n}e^{\left(a+b\right)t}=\sum_{k=0}^{n}\binom{n}{k}a^{k}e^{at}b^{n-k}e^{bt}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-52bbeb4c6a5c1104e8f9b46e5de8736e_l3.png)
![Rendered by QuickLaTeX.com \[\left(a+b\right)^{n}=\sum_{k=0}^{n}\binom{n}{k}a^{k}b^{n-k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-96efa5408ea34faae09d7053a97a21d4_l3.png)
On a démontré la formule du binôme (dans le champ réel) en partant de la formule de Leibniz.
Et dans l’autre sens ? Voyons …
4 – Déduire  de
de  : pas commode !
: pas commode !
A présent, on suppose connue la formule du binôme dans un anneau (c’est-à-dire la version générale décrite à la section 1).
Considérons le ![]() -espace vectoriel
-espace vectoriel ![]() et l’anneau
et l’anneau ![]()
Les vecteurs de ![]() sont donc les applications indéfiniment différentiables de
sont donc les applications indéfiniment différentiables de ![]() dans
dans ![]()
Quant aux éléments de ![]() ce sont les endomorphismes de
ce sont les endomorphismes de ![]() Parmi eux se trouvent les endomorphismes de dérivation partielle
Parmi eux se trouvent les endomorphismes de dérivation partielle ![]() et
et ![]() , qui commutent d’après le théorème de Schwarz .
, qui commutent d’après le théorème de Schwarz .
On peut donc appliquer la formule du binôme :
(![]() )
) ![Rendered by QuickLaTeX.com \[\left(\frac{\partial}{\partial x}+\frac{\partial}{\partial y}\right)^{n}=\sum_{k=0}^{n}\,\binom{n}{k}\,\frac{\partial^{n}}{\partial x^{k}\,\partial y^{n-k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5fd753c3b46de3430d7970da457994d5_l3.png)

ATTENTION !
Les deux membres de l’égalité ci-dessus appartiennent à l’anneau ![]()
Etant données ![]() de classe
de classe ![]() appliquons
appliquons ![]() à
à ![]() définie par :
définie par :
![]()
![Rendered by QuickLaTeX.com \[\left(\frac{\partial}{\partial x}+\frac{\partial}{\partial y}\right)^{n}\left(f\otimes g\right)=\sum_{k=0}^{n}\,\binom{n}{k}\,f^{\left(k\right)}\otimes g^{\left(n-k\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-659094fabeeb01ab0f3971e073917516_l3.png)
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\left(fg\right)^{\left(n\right)} & = \left[\left(\frac{\partial}{\partial x}+\frac{\partial}{\partial y}\right)^{n}\circ\psi\right]\left(f\otimes g\right)\\& = \left[\psi\circ\left(\frac{\partial}{\partial x}+\frac{\partial}{\partial y}\right)^{n}\right]\left(f\otimes g\right)\end{split}\end{equation*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-6eecc475d32b32576b868fa46c544682_l3.png)
![Rendered by QuickLaTeX.com \[\left(fg\right)^{\left(n\right)}=\sum_{k=0}^{n}\,\binom{n}{k}\,\psi\left(f^{\left(k\right)}\otimes g^{\left(n-k\right)}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7a248645ec2f160b05ed47cefd26df60_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\left(fg\right)^{\left(n\right)}=\sum_{k=0}^{n}\,\binom{n}{k}\,f^{\left(k\right)}\,g^{\left(n-k\right)}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cbbc059ce7466ed71fdcffb443e251eb_l3.png)
Pas commode, en effet … mais on a bien établi la formule de Leibniz en partant de la formule du binôme.
Remarque
En mathématiques, il est fréquent qu’un « élargissement du contexte » permette de démontrer confortablement un résultat qui s’énonce a priori dans un contexte plus restreint. Par exemple, une somme de nombres réels peut parfois être calculée plus commodément en étant considérée comme la partie réelle ou imaginaire d’une somme de nombres complexes. Cette situation apparaît par exemple à l’exercice n° 6 de cette fiche d’exercices.
C’est ce qui s’est produit dans la preuve de la formule de Leibniz qu’on vient de voir : un problème concernant des fonctions d’une seule variable a été résolu en passant par un contexte plus large, faisant intervenir des fonctions de deux variables !
5 – On prend de la hauteur…
Dans l’introduction, nous nous sommes demandés s’il existait un résultat général englobant les formules ![]() et
et ![]() comme des cas particuliers. Voici un élément de réponse :
comme des cas particuliers. Voici un élément de réponse :
Lemme
Soit ![]() un anneau commutatif.
un anneau commutatif.
On considère un ![]() module
module ![]() ainsi qu’un morphisme
ainsi qu’un morphisme ![]() .
.
Si ![]() est une famille d’éléments de
est une famille d’éléments de ![]() vérifiant :
vérifiant :
![]()
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\forall n\in\mathbb{N},\thinspace f^{n}\left(T_{0,0}\right)=\displaystyle{\sum_{k=0}^{n}\binom{n}{k}T_{k,n-k}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c722f14a9b68262f686be076ba3b4dfb_l3.png)
La preuve se fait par récurrence sur ![]() via la formule de Pascal pour les coefficients binomiaux, exactement selon le modèle déjà expliqué plus haut.
via la formule de Pascal pour les coefficients binomiaux, exactement selon le modèle déjà expliqué plus haut.
Voici maintenant deux cas particuliers qui nous intéressent :
Cas particulier n° 1
Etant donné un anneau commutatif ![]() :
:
- on choisit
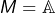 et l’on fixe
et l’on fixe 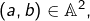
- on choisit
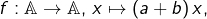
- on pose
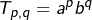 pour tout
pour tout 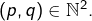
➣ on retrouve la formule du binôme (dans le cas d’un anneau \textbf{\emph{commutatif}}).
Cas particulier n° 2
Avec ![]() :
:
- on choisit
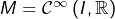 où
où 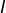 est un intervalle non trivial et l’on fixe
est un intervalle non trivial et l’on fixe 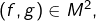
- on choisit
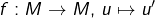 (morphisme de dérivation)
(morphisme de dérivation) - on pose
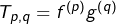 pour tout
pour tout 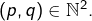
➣ on retrouve la formule de Leibniz.
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Wha plutôt chouette ! merci pour l’article