
Dans cet article, je vous propose un tour d’horizon des principales méthodes utilisées pour établir l’injectivité ou la surjectivité d’une application. Si ces notions vous sont peu familières, les deux vidéos suivantes pourront vous aider (on y trouve les principales définitions et des exemples simples) :
☞ Correspondances, Fonctions, Applications — Partie 1
☞ Correspondances,Fonctions, Applications — Partie 2
Dans ce qui suit, les notions suivantes sont supposées connues :
ensemble, élément, application, ensemble de départ ou d’arrivée, image, antécédents.
1 – Injectivité
Définition
Etant donnés deux ensembles ![]() ainsi qu’une application
ainsi qu’une application ![]() on dit que
on dit que ![]() est injective (ou bien que
est injective (ou bien que ![]() est une injection) lorsque deux éléments distincts de
est une injection) lorsque deux éléments distincts de ![]() possèdent nécessairement des images distinctes par
possèdent nécessairement des images distinctes par ![]()
En d’autres termes, ![]() est injective lorsque deux éléments de
est injective lorsque deux éléments de ![]() ayant la même image par
ayant la même image par ![]() sont nécessairement égaux. Cette seconde formulation (contraposée de la précédente) se formalise ainsi :
sont nécessairement égaux. Cette seconde formulation (contraposée de la précédente) se formalise ainsi :
![]()
Pour les démonstrations d’injectivité, on préfère généralement recourir à cette version, car la relation d’égalité possède de « bonnes propriétés » que la relation « être différent de » ne possède pas. Notamment :
- elle est transitive (si
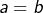 et
et 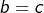 , alors
, alors  ), alors que, bien entendu, les conditions
), alors que, bien entendu, les conditions 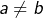 et
et 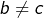 n’impliquent pas
n’impliquent pas 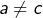 .
. - des égalités entre nombres réels (ou complexes) peuvent être ajoutées membre à membre, alors que cette procédure est illicite avec la relation « différent de ». Par exemple :
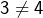 et
et 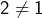 mais
mais 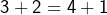 . Même remarque avec la multiplication membre à membre.
. Même remarque avec la multiplication membre à membre.
Bref, afin de prouver qu’une application est injective, vous devrez généralement considérer deux éléments de l’ensemble de départ possédant la même image, puis faire votre possible pour montrer qu’ils sont nécessairement égaux.
Voir à ce sujet l’article Viser la cible !… ou : Comment démontrer une implication ?
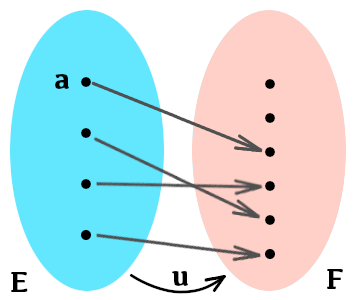
Si l’on s’autorise l’utilisation d’un diagramme sagittal (deux patates et des flèches …), la condition d’injectivité signifie que jamais deux flèches issues de l’ensemble de départ n’aboutissent en un même élément de l’ensemble d’arrivée :
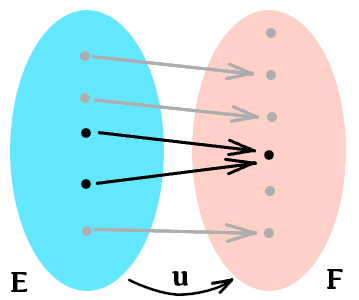
2 – Exemples
Exemple 1
L’application
![]()
Exemple 2
L’application « partie entière »
![]()
En effet : ![]() et
et ![]()
Avant de poursuivre, arrêtons-nous un instant sur un point de logique.

Pour justifier la non-injectivité d’une application, il suffit d’exhiber un seul couple formé de deux éléments distincts et possédant la même image.
Pour le premier exemple, j’ai choisi le couple ![]() et pour le second, j’ai opté pour
et pour le second, j’ai opté pour ![]()
En revanche, pour faire la preuve de l’injectivité d’une application, examiner quelques exemples ne suffira pas ! Il faut absolument considérer un couple quelconque d’éléments de l’ensemble de départ et montrer que s’ils ont la même image, alors ils sont égaux. Les deux exemples qui suivent illustrent ce point. Le premier est rudimentaire, le second est un peu plus élaboré.
Exemple 3
L’application
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$f:\mathbb{R}-\left\{ 2\right\} \rightarrow\mathbb{R},\thinspace x\mapsto\dfrac{4x-1}{x-2}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0cec7a13dc8188bda2e6084a3672242a_l3.png)
![]()
![]()
![]()
Exemple 4
Montrons que l’application
![]()
![]()
![]()
![]()
Précisons que l’application ![]() n’est pas injective ! En effet :
n’est pas injective ! En effet : ![]() mais ces deux nombres complexes ont le même cube.
mais ces deux nombres complexes ont le même cube.
Voici un cinquième exemple, plus abstrait. En outre, les ensembles de départ et d’arrivée ne sont plus des parties de ![]() …
…
Exemple 5
Notons ![]() l’ensemble des applications de
l’ensemble des applications de ![]() dans lui-même et intéressons-nous à l’application :
dans lui-même et intéressons-nous à l’application :
![]()
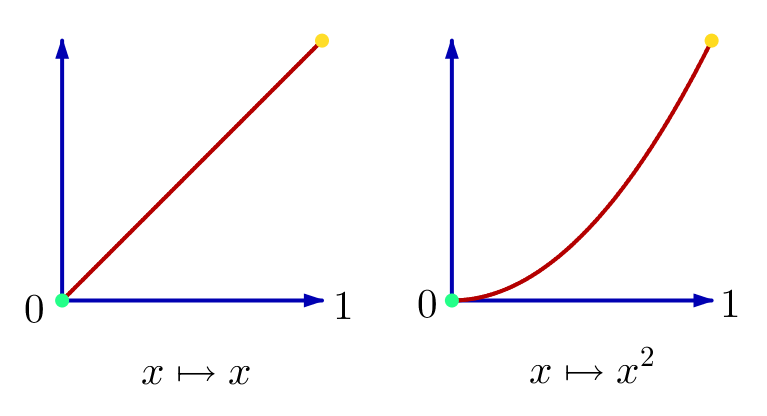
En considérant ![]() et
et ![]() on constate que
on constate que ![]() bien que
bien que ![]() Ceci prouve que
Ceci prouve que ![]() n’est pas injective.
n’est pas injective.
Maintenant, notons ![]() la restriction de
la restriction de ![]() à l’ensemble des applications affines (rappel : les applications affines sont celles de la forme
à l’ensemble des applications affines (rappel : les applications affines sont celles de la forme ![]() avec
avec ![]() arbitraire).
arbitraire).
Soient ![]() deux applications affines telles que
deux applications affines telles que ![]()
En posant, pour tout ![]() :
:
![]()
Ceci prouve l’injectivité de ![]()
Remarque
On aurait pu s’intéresser aux noyaux de ![]() et
et ![]() après avoir constaté leur linéarité.
après avoir constaté leur linéarité.
3 – Surjectivité
Définition
On dit qu’une application ![]() est surjective (ou bien : que c’est une surjection) lorsque tout élément
est surjective (ou bien : que c’est une surjection) lorsque tout élément ![]() de
de ![]() admet (au moins) un antécédent par
admet (au moins) un antécédent par ![]()
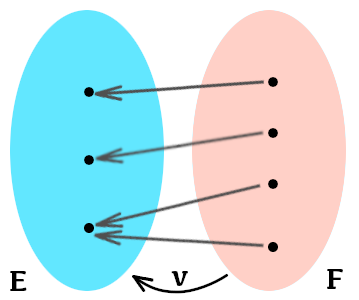
Visuellement, chaque élément de l’ensemble d’arrivée doit être atteint par une flèche (au moins) provenant de l’ensemble de départ :
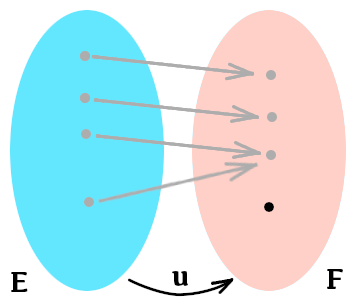
Voici la version formalisée de la définition :
![]()
Prouver, en appliquant cette définition, qu’une application ![]() est surjective, consiste à se donner un élément
est surjective, consiste à se donner un élément ![]() quelconque (dans l’ensemble d’arrivée) puis à remuer ciel et terre pour établir l’existence d’un élément
quelconque (dans l’ensemble d’arrivée) puis à remuer ciel et terre pour établir l’existence d’un élément ![]() (dans l’ensemble de départ) vérifiant
(dans l’ensemble de départ) vérifiant ![]()
Pour le dire encore autrement : il s’agit de montrer que, pour tout ![]() l’équation
l’équation ![]() (d’inconnue
(d’inconnue ![]() possède au moins une solution.
possède au moins une solution.
Dans certains cas simples, il est possible d’exhiber (au moyen d’une formule) une solution à cette équation. Par exemple, si l’on considère l’application
![]()
![]()
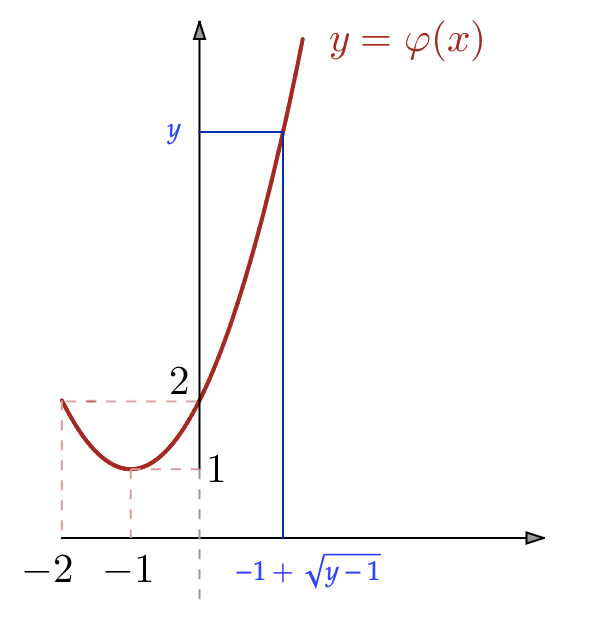
Ainsi, ![]() est surjective (mais non injective, soit dit en passant, puisque les éléments de
est surjective (mais non injective, soit dit en passant, puisque les éléments de ![]() possèdent deux antécédents par
possèdent deux antécédents par ![]() à savoir
à savoir ![]() et
et ![]()
L’exemple ci-dessus doit être considéré comme exceptionnel, car le calcul explicite d’un antécédent reste en général hors de portée. Les choses deviennent alors subtiles : il faut montrer que l’équation ![]() possède au moins une solution, mais sans pouvoir en expliciter aucune !
possède au moins une solution, mais sans pouvoir en expliciter aucune !
Par exemple, dans le cas de ![]() il n’est pas possible de résoudre l’équation
il n’est pas possible de résoudre l’équation ![]() , sauf dans des cas particuliers (
, sauf dans des cas particuliers (![]() par exemple : on voit tout de suite que
par exemple : on voit tout de suite que ![]() convient).
convient).
On contourne cette difficulté en invoquant le théorème des valeurs intermédiaires. En effet, pour tout ![]() l’application
l’application ![]() est continue et ses limites en
est continue et ses limites en ![]() et
et ![]() sont respectivement
sont respectivement ![]() et
et ![]() ce qui assure l’existence d’un réel
ce qui assure l’existence d’un réel ![]() tel que
tel que ![]() c’est-à-dire un antécédent pour
c’est-à-dire un antécédent pour ![]()
4 – Encore des exemples
Exemple 1
L’application
![]()
Exemple 2
L’application
![]()
En effet, étant donné ![]() si
si ![]() il suffit de choisir
il suffit de choisir ![]() et, si
et, si ![]() il suffit de choisir
il suffit de choisir ![]()
Ajoutons que cette application est loin d’être injective, puisque si le couple ![]() est antécédent d’un certain
est antécédent d’un certain ![]() alors le couple
alors le couple ![]() aussi, et ceci pour tout
aussi, et ceci pour tout ![]() Tout nombre réel possède donc une infinité d’antécédents !
Tout nombre réel possède donc une infinité d’antécédents !
Exemple 3
Notons ![]() l’ensemble des entiers supérieurs ou égaux à 2. L’application
l’ensemble des entiers supérieurs ou égaux à 2. L’application
![]()
Ajoutons que cette application n’est pas injective puisque ![]() et
et ![]() ont la même image.
ont la même image.
Exemple 4
Considérons enfin l’application
![]()
![]()
Voici encore un exemple où la surjectivité d’une application est établie de façon indirecte. Mais en l’occurrence, une preuve directe est facile à produire. En effet, quels que soient les réels ![]() et
et ![]() le quadruplet :
le quadruplet :
![]()
5 – On récapitule …
Marquons une courte pause et reformuleons de manière un peu différente et surtout plus synthétique, ce que nous avons vu jusqu’ici :
➡ Dire que ![]() est injective signifie que :
est injective signifie que :
tout élément de ![]() possède au plus un antécédent par
possède au plus un antécédent par ![]()
➡ Dire que ![]() est surjective signifie que :
est surjective signifie que :
tout élément de ![]() possède au moins un antécédent par
possède au moins un antécédent par ![]()
L’écart entre les deux notions tient donc simplement au remplacement d’un mot par un autre …
Que se passe-t-il lorsqu’on superpose les deux conditions ? Autrement dit, que dire d’une application qui serait à la fois injective et surjective ?
Une telle application s’appelle, par définition, une bijection.
Observons que cette condition signifie :
- d’une part, que tout élément de l’ensemble de départ possède une image et une seule (mais cela n’est rien d’autre que la définition d’une application),
- d’autre part, que tout élément de l’ensemble d’arrivée possède un antécédent et un seul (résultat de la superposition des locutions « au plus » et « au moins »).
Une bijection est donc ce qu’on pourrait appeler une « correspondance parfaite » entre les ensembles ![]() et
et ![]() Pour en savoir davantage à ce sujet, on pourra consulter l’article Qu’est-ce qu’une bijection, au juste ?
Pour en savoir davantage à ce sujet, on pourra consulter l’article Qu’est-ce qu’une bijection, au juste ?
6 – Composition d’injections ou de surjections
On considère ici trois ensembles ![]() et
et ![]() ainsi que deux applications
ainsi que deux applications ![]() et
et ![]()
Rappelons par précaution que l’application ![]() est appelée la composée de
est appelée la composée de ![]() par
par ![]() et notée
et notée ![]() (ce qu’on lit « v rond u »).
(ce qu’on lit « v rond u »).
La proposition suivante nous apporte quatre petites propriétés à la fois très simples et très utiles :
Proposition
Injectivité ou surjectivité d’une composée :
(1) Si ![]() et
et ![]() sont injectives, alors
sont injectives, alors ![]() aussi.
aussi.
(2) Si ![]() et
et ![]() sont surjectives, alors
sont surjectives, alors ![]() aussi.
aussi.
(3) Si ![]() est injective, alors
est injective, alors ![]() aussi.
aussi.
(4) Si ![]() est surjective, alors
est surjective, alors ![]() aussi.
aussi.
Preuve (cliquer pour déplier / replier)
Pour (1) : si ![]() sont tels que
sont tels que ![]() alors
alors ![]() (car
(car ![]() est injective) et donc
est injective) et donc ![]() (car
(car ![]() est injective). Ceci prouve l’injectivité de
est injective). Ceci prouve l’injectivité de ![]()
Pour (2) : si ![]() alors il existe
alors il existe ![]() tel que
tel que ![]() (car
(car ![]() est surjective) puis (comme
est surjective) puis (comme ![]() est surjective) il existe
est surjective) il existe ![]() tel que
tel que ![]() Ainsi
Ainsi ![]() et ceci prouve la surjectivité de
et ceci prouve la surjectivité de ![]()
Pour (3) : si ![]() sont tels que
sont tels que ![]() alors
alors ![]() et donc, comme
et donc, comme ![]() est injective, il s’ensuit que
est injective, il s’ensuit que ![]() Ceci montre l’injectivité de
Ceci montre l’injectivité de ![]()
Enfin, pour (4) : si ![]() alors il existe par surjectivité de
alors il existe par surjectivité de ![]() un élément
un élément ![]() tel que
tel que ![]() En posant
En posant ![]() on constate que
on constate que ![]() et que
et que ![]() ceci montre la surjectivité de
ceci montre la surjectivité de ![]()
Avec les mêmes notations, on en déduit des points (3) et (4) précédents que :
Corollaire
Si ![]() est bijective, alors
est bijective, alors ![]() est injective et
est injective et ![]() et surjective.
et surjective.
Un cas particulier important est celui où ![]() vérifie
vérifie ![]() , c’est-à-dire :
, c’est-à-dire :
![]()
Une telle application est dite involutive (on dit aussi qu’il s’agit d’une involution).
Vu que l’application identique est bijective, on voit qu’une involution est nécessairement injective et surjective, donc bijective.
7 – Injectivité et stricte monotonie
Limitons nous ici au cas d’une application ![]() où
où ![]() sont deux parties non vides de
sont deux parties non vides de ![]()
Rappelons que ![]() est dite strictement croissante lorsque, pour tout couple
est dite strictement croissante lorsque, pour tout couple ![]() d’éléments de
d’éléments de ![]() l’hypothèse
l’hypothèse ![]() entraîne
entraîne ![]()
La stricte décroissance est définie de manière analogue et ![]() est dite strictement monotone lorsqu’elle est soit strictement croissante, soit strictement décroissante.
est dite strictement monotone lorsqu’elle est soit strictement croissante, soit strictement décroissante.
De manière évidente :
Proposition
Dans le contexte défini ci-dessus, la stricte monotonie entraîne l’injectivité.
Ce résultat, bien que rudimentaire, est très utile. C’est ainsi que l’injectivité de l’application
![]()
Quant à la réciproque de l’implication
![]()
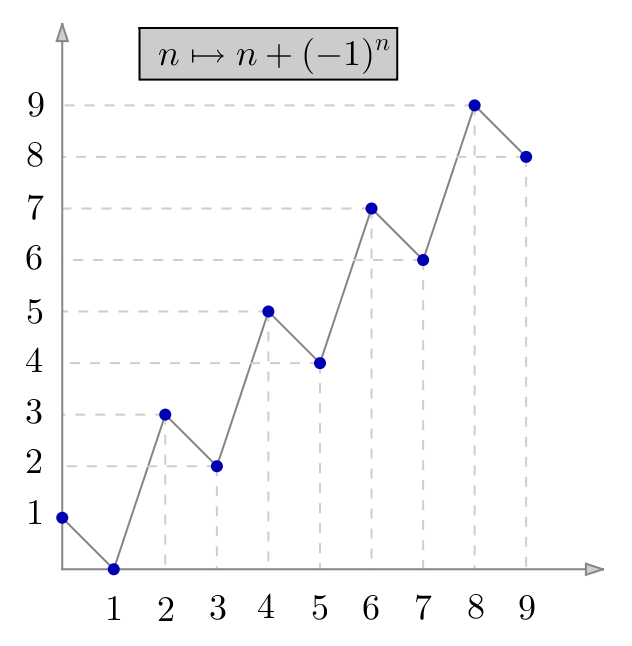
- Considérons deux entiers naturels
 distincts et envisageons deux cas, pour montrer qu’ils possèdent des images distinctes :
distincts et envisageons deux cas, pour montrer qu’ils possèdent des images distinctes :- Si
 et
et  sont de même parité, alors leurs images respectives sont
sont de même parité, alors leurs images respectives sont  et
et  (s’ils sont tous deux pairs) ou bien
(s’ils sont tous deux pairs) ou bien  et
et  (s’ils sont tous deux impairs) donc sont distinctes.
(s’ils sont tous deux impairs) donc sont distinctes. - Si
 et
et 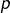 sont de parités contraires, alors c’est encore le cas de leurs images (car ajouter ou retrancher 1 à un entier inverse sa parité), qui sont donc distinctes.
sont de parités contraires, alors c’est encore le cas de leurs images (car ajouter ou retrancher 1 à un entier inverse sa parité), qui sont donc distinctes.
- Si
- Comme
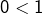 et
et 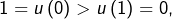 on voit que
on voit que  n’est pas croissante. Et comme
n’est pas croissante. Et comme 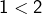 et
et 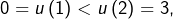 on voit qu’elle n’est pas décroissante non plus.
on voit qu’elle n’est pas décroissante non plus.
Le premier point montre que la suite ![]() est injective, et le second qu’elle est non monotone (plus précisément, elle n’est monotone à partir d’aucun rang).
est injective, et le second qu’elle est non monotone (plus précisément, elle n’est monotone à partir d’aucun rang).
La situation serait-t-elle différente sans le cas où ![]() et
et ![]() sont des intervalles ? L’exemple qui suit montre que non …
sont des intervalles ? L’exemple qui suit montre que non …
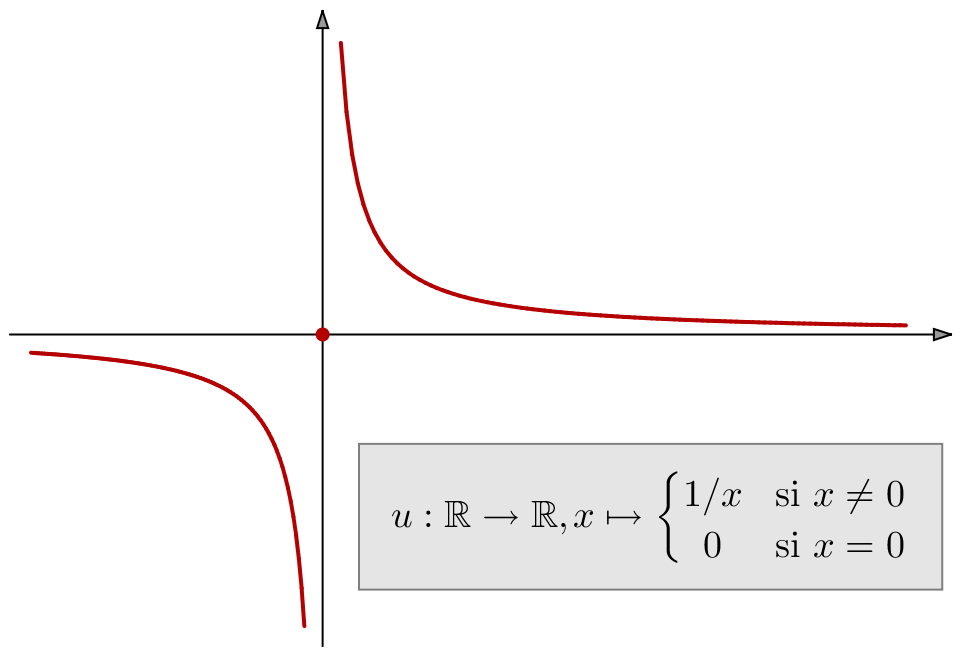
Cette application est une involution donc d’une bijection (voir fin de la section 6) et, en particulier, une injection. Pour autant, ![]() n’est pas strictement monotone. En effet :
n’est pas strictement monotone. En effet :
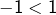 et
et 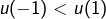 donc
donc  n’est pas strictement décroissante,
n’est pas strictement décroissante,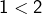 et
et 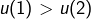 donc
donc  n’est pas strictement croissante.
n’est pas strictement croissante.
Toutefois, un joli théorème nous apporte une réciproque partielle :
Théorème
Si ![]() est un intervalle (de longueur non nulle) et si
est un intervalle (de longueur non nulle) et si ![]() est continue et injective, alors
est continue et injective, alors ![]() est strictement monotone.
est strictement monotone.
Preuve (cliquer pour déplier / replier)
Soient ![]() tels que
tels que ![]() . Comme
. Comme ![]() est injective, alors
est injective, alors ![]() Supposons dans la suite de cette preuve que
Supposons dans la suite de cette preuve que ![]() et montrons que
et montrons que ![]() est strictement croissante (dans le cas où
est strictement croissante (dans le cas où ![]() il suffit d’appliquer ce qui va suivre à
il suffit d’appliquer ce qui va suivre à ![]() pour conclure que
pour conclure que ![]() est strictement croissante, et donc que
est strictement croissante, et donc que ![]() est strictement décroissante).
est strictement décroissante).
Soient ![]() tels que
tels que ![]()
Afin de prouver que ![]() considérons l’application auxiliaire :
considérons l’application auxiliaire :
![]()
Dans le cas contraire, il existerait ![]() tel que :
tel que :
![]()
![]()
![]()
Mais
Or, ![]() donc
donc ![]() soit finalement :
soit finalement : ![]()
8 – Dans un sens ou dans l’autre …
La proposition suivante indique un lien intéressant entre les notions d’injectivité et de surjectivité :
Proposition
Soient ![]() et
et ![]() deux ensembles non vides. Alors l’existence d’une injection
deux ensembles non vides. Alors l’existence d’une injection ![]() équivaut à l’existence d’une surjection
équivaut à l’existence d’une surjection ![]()
Preuve (cliquer pour déplier / replier)
Supposons l’existence d’une injection ![]() On peut alors construire une surjection
On peut alors construire une surjection ![]() de la manière suivante. On commence par choisir un élément
de la manière suivante. On commence par choisir un élément ![]() Pour chaque élément
Pour chaque élément ![]() de
de ![]() on envisage deux cas :
on envisage deux cas :
- si
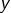 possède un antécédent par
possède un antécédent par 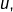 on sait que celui-ci est unique (hypothèse d’injectivité). Notons-le
on sait que celui-ci est unique (hypothèse d’injectivité). Notons-le  et posons :
et posons : 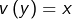
- si
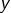 ne possède pas d’antécédent par
ne possède pas d’antécédent par 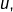 posons
posons 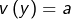
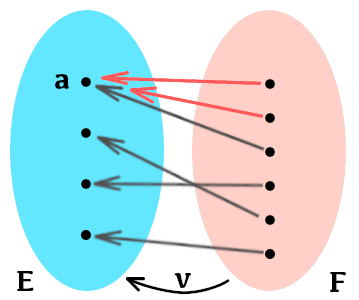
L’application ![]() ainsi définie est surjective puisque
ainsi définie est surjective puisque ![]()
Supposons maintenant l’existence d’une surjection ![]() Pour chaque élément
Pour chaque élément ![]() choisissons l’un ses antécédents (il en existe : hypothèse de surjectivité) et notons-le
choisissons l’un ses antécédents (il en existe : hypothèse de surjectivité) et notons-le ![]() (et ne nous cachons pas derrière notre petit doigt : nous sommes en train d’utiliser l’axiome du choix).
(et ne nous cachons pas derrière notre petit doigt : nous sommes en train d’utiliser l’axiome du choix).
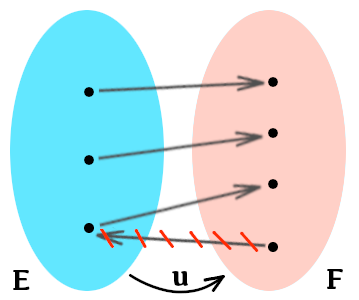
L’application ![]() ainsi définie est injective puisque
ainsi définie est injective puisque ![]()
Dans le cas d’ensembles finis, l’existence d’une injection ![]() équivaut à la condition
équivaut à la condition ![]() Rappelons que le nombre d’éléments d’un ensemble fini
Rappelons que le nombre d’éléments d’un ensemble fini ![]() est appelé le cardinal de
est appelé le cardinal de ![]() et noté
et noté ![]()
De même, l’existence d’une surjection ![]() équivaut à la condition
équivaut à la condition ![]() Ceci rend évidente la proposition ci-dessus, au moins pour des ensembles
Ceci rend évidente la proposition ci-dessus, au moins pour des ensembles ![]() finis. Et il est intéressant de noter que sa validité persiste en général (pour des ensembles non supposés finis).
finis. Et il est intéressant de noter que sa validité persiste en général (pour des ensembles non supposés finis).
Cette remarque peut en évoquer une autre, à savoir que (toujours pour des ensembles finis) l’existence simultanée d’une injection ![]() et d’une injection
et d’une injection ![]() se traduit par une double inégalité entre les cardinaux, autrement dit par l’équipotence des deux ensembles
se traduit par une double inégalité entre les cardinaux, autrement dit par l’équipotence des deux ensembles ![]() et
et ![]() (deux ensembles sont dits équipotents lorsqu’il existe une bijection de l’un vers l’autre. Dans le cas d’ensembles finis, cette condition équivaut à l’égalité des cardinaux). Là encore, il est frappant de constater que la propriété reste vraie pour des ensembles non supposés finis, mais la preuve est beaucoup plus délicate. Pour en savoir plus à ce sujet, on pourra consulter l’article le théorème de Cantor-Bernstein-Schröder.
(deux ensembles sont dits équipotents lorsqu’il existe une bijection de l’un vers l’autre. Dans le cas d’ensembles finis, cette condition équivaut à l’égalité des cardinaux). Là encore, il est frappant de constater que la propriété reste vraie pour des ensembles non supposés finis, mais la preuve est beaucoup plus délicate. Pour en savoir plus à ce sujet, on pourra consulter l’article le théorème de Cantor-Bernstein-Schröder.
9 – Intervention d’une hypothèse de finitude
Rappelons qu’un espace vectoriel ![]() est dit « de dimension finie » lorsqu’il est engendré par une famille finie de vecteurs. On montre alors qu’il existe des familles finies qui sont à la fois libres et génératrices de
est dit « de dimension finie » lorsqu’il est engendré par une famille finie de vecteurs. On montre alors qu’il existe des familles finies qui sont à la fois libres et génératrices de ![]() Ces sont les bases de
Ces sont les bases de ![]() En outre, toutes les bases sont composées d’un même nombre
En outre, toutes les bases sont composées d’un même nombre ![]() de vecteurs. Cet entier
de vecteurs. Cet entier ![]() est appelé la dimension de
est appelé la dimension de ![]() et noté
et noté ![]()
Voici deux propositions « jumelles », données ici sans démonstration (la seconde est un corollaire bien connu du théorème du rang) :
Proposition ✧
On considère deux ensembles finis ![]() On suppose que
On suppose que ![]() et l’on considère une application
et l’on considère une application ![]() Alors :
Alors :
![]()
Proposition ✦
On considère deux espaces vectoriels ![]() et
et ![]() (sur un même corps
(sur un même corps ![]() On suppose qu’ils sont de même dimension finie et l’on considère une application linéaire
On suppose qu’ils sont de même dimension finie et l’on considère une application linéaire ![]() Alors :
Alors :
![]()
Donnons, pour chacune de ces propositions, deux exemples d’utilisation :
Exemple ✧1
Soient ![]() deux entiers naturels non nuls, premiers entre eux (c’est-à-dire tels que
deux entiers naturels non nuls, premiers entre eux (c’est-à-dire tels que ![]()
On note classiquement ![]() l’ensemble des entiers de 1 à
l’ensemble des entiers de 1 à ![]() et l’expression
et l’expression ![]() désigne (non moins classiquement) le reste de la division euclidienne de
désigne (non moins classiquement) le reste de la division euclidienne de ![]() par
par ![]()
Montrons que l’application
![]()
Avant toute chose, rappelons que ![]() pour tout entier
pour tout entier ![]() ce qui montre que
ce qui montre que ![]() est bien à valeurs dans
est bien à valeurs dans ![]()
Pour prouver la surjectivité de ![]() l’idée consiste à établir plutôt son injectivité, puis à invoquer la proposition ✧ …
l’idée consiste à établir plutôt son injectivité, puis à invoquer la proposition ✧ …
Soient donc ![]() tels que :
tels que :
![]()
![]()
Exemple ✧2
Considérons un groupe fini ![]() de cardinal impair et notons
de cardinal impair et notons ![]() son élément neutre. Montrons que :
son élément neutre. Montrons que :
![]()
Introduisons l’application
![]()
Il s’agit d’établir sa bijectivité.
Etant donné ![]() l’ordre
l’ordre ![]() de
de ![]() est impair puisque c’est un diviseur de
est impair puisque c’est un diviseur de ![]() Notons
Notons ![]() et posons
et posons ![]() Vu que
Vu que ![]() (conséquence du théorème de Lagrange ! Voir à ce sujet la vidéo
(conséquence du théorème de Lagrange ! Voir à ce sujet la vidéo
Théorème de Lagrange et ordre d’un élément dans un groupe fini), on constate que :
![]()
Exemple ✦1
Fixons un entier ![]() et considérons deux sous-espaces vectoriels de l’espace
et considérons deux sous-espaces vectoriels de l’espace ![]() des matrices carrées réelles de taille
des matrices carrées réelles de taille ![]() :
:
- l’ensemble
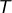 des matrices triangulaires supérieures
des matrices triangulaires supérieures - l’ensemble
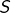 des matrices symétriques
des matrices symétriques
L’application :
![]()
Si ![]() appartient au noyau, alors
appartient au noyau, alors ![]() est à la fois triangulaire supérieure et antisymétrique, donc nulle. De ce fait,
est à la fois triangulaire supérieure et antisymétrique, donc nulle. De ce fait, ![]() est injective et donc bijective puisque :
est injective et donc bijective puisque :
![]()
Terminons avec un exemple tiré du cours d’algèbre bilinéaire …
Exemple ✦2
Soit ![]() un espace vectoriel euclidien, c’est-à-dire un
un espace vectoriel euclidien, c’est-à-dire un ![]() espace vectoriel de dimension finie, muni d’un produit scalaire. Le produit scalaire de deux vecteurs
espace vectoriel de dimension finie, muni d’un produit scalaire. Le produit scalaire de deux vecteurs ![]() est noté
est noté ![]()
On note encore ![]() le dual de
le dual de ![]() c’est-à-dire l’espace des formes linéaires sur
c’est-à-dire l’espace des formes linéaires sur ![]()
Dans ce contexte, considérons l’application linéaire
![]()
Si ![]() alors
alors ![]() pour tout
pour tout ![]() En particulier
En particulier ![]() et donc
et donc ![]() Ceci montre que
Ceci montre que ![]() est injective.
est injective.
Mais comme ![]() il s’ensuit que
il s’ensuit que ![]() est surjective.
est surjective.
Ainsi, ![]() est un isomorphisme (appelé isomorphisme canonique entre un espace vectoriel euclidien et son dual).
est un isomorphisme (appelé isomorphisme canonique entre un espace vectoriel euclidien et son dual).
Ce thème est abordé plus en détail dans l’exercice n° 2 de la fiche Exercices sur le produit scalaire – 01
J’espère que cet article vous aura permis de mieux maîtriser les méthodes de base pour montrer qu’une application est (ou n’est pas) injective ou surjective.
N’hésitez pas à me laisser vos questions et remarques en commentaires ou bien en passant par le formulaire de contact.
