
Dans cet article, je vous propose d’étudier des exemples de résolution d’équations à une inconnue, dans le champ réel. Après avoir introduit le vocabulaire usuel et présenté un cadre général, nous limiterons celui-ci aux équations algébriques de petit degré.
De quoi s’agit-il ?
Une équation est simplement une égalité dans laquelle figure une inconnue (que l’on désigne par une lettre, souvent la lettre ‘x’, mais cela n’est pas obligatoire).
But du jeu : déterminer les solutions de cette équation, c’est-à-dire les valeurs (réelles) que l’on peut attribuer à l’inconnue de telle sorte que l’égalité soit vérifiée.
L’ensemble des solutions, que l’on peut noter ![]() est une partie de
est une partie de ![]() qui peut très bien être vide. C’est le cas pour l’équation
qui peut très bien être vide. C’est le cas pour l’équation ![]() C’est aussi le cas pour l’équation
C’est aussi le cas pour l’équation ![]() .
.
Et lorsque ![]() est non vide, on cherche à en déterminer les éléments, de façon exacte. Cependant, il est fréquent (même pour des équations d’apparence très simple) que cet objectif ne soit pas accessible. On peut alors se contenter d’une information réduite, en répondant par exemple aux questions suivantes :
est non vide, on cherche à en déterminer les éléments, de façon exacte. Cependant, il est fréquent (même pour des équations d’apparence très simple) que cet objectif ne soit pas accessible. On peut alors se contenter d’une information réduite, en répondant par exemple aux questions suivantes :
- combien de solutions existe-t-il ?
- peut-on obtenir, pour chacune d’elles, un encadrement arbitrairement fin ?
Dans tout ce qui suit, on se limitera à des situations se ramenant à des équations du second degré. Ce cadre sera toutefois quelque peu élargi, à la section 4.
Un prochain article (de niveau lycée également) abordera l’étude d’équations trigonométriques.
Le décor est posé. Commençons par un exemple que ne devrait soulever aucune difficulté.
1 – Exemple Introductif
Il s’agit de l’équation du second degré suivante :
(![]() )
) ![]()
![]()
![]()
On commence par observer que l’équation ![]() peut s’écrire :
peut s’écrire :
![]()
![]()
![]()
![]()
![]()
2 – Théorie générale
Dans cette section, on généralise ce qui précède en présentant la théorie (pas de panique !.. c’est une théorie bien modeste) des équations de la forme :
![]()
![]() Si
Si ![]() l’équation est en quelque sorte dégénérée (l’inconnue n’y figure même plus !). La question peut même paraître assez étrange, voire absurde :
l’équation est en quelque sorte dégénérée (l’inconnue n’y figure même plus !). La question peut même paraître assez étrange, voire absurde :
Quelles sont les valeurs de ![]() pour lesquelles
pour lesquelles ![]() ?
?
Etrange en effet… mais parfaitement envisageable ! Et la réponse est :
- toutes, si
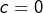
- aucune, si
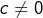
En d’autres termes, si l’on note ![]() l’ensemble des solutions de l’équation
l’ensemble des solutions de l’équation ![]() , alors :
, alors :
![]()
![]() Si
Si ![]() , on obtient l’équation du premier degré suivante :
, on obtient l’équation du premier degré suivante :
![]()
![]()
![]() Si
Si ![]() l’équation est dite du second degré. J’ai consacré en 2010, trois vidéos à ce thème (les deux premières abordent, comme ici, l’étude dans le champ réel. La troisième envisage la résolution dans le champ complexe et dépasse donc le cadre du présent article). Je vous invite à les visionner :
l’équation est dite du second degré. J’ai consacré en 2010, trois vidéos à ce thème (les deux premières abordent, comme ici, l’étude dans le champ réel. La troisième envisage la résolution dans le champ complexe et dépasse donc le cadre du présent article). Je vous invite à les visionner :
Toutefois, afin de préserver l’unité de la présentation, les calculs vont maintenant être détaillés, en conservant les notations adoptées plus haut.
L’idée principale consiste à transformer l’équation ![]() pour la mettre sous forme canonique.
pour la mettre sous forme canonique.
L’adjectif « canonique » est à prendre au sens de standard. C’est ainsi que l’on nomme l’écriture suivante, qui est équivalente à ![]() :
:
(![]() )
) ![]()
L’intérêt de mettre l’équation sous cette nouvelle forme est clair : on cherche à faire apparaître une différence de deux carrés (exactement comme dans l’exemple particulier traité à la section 1).
C’est bien parti, puisque le membre de gauche de ![]() est la différence entre le carré de
est la différence entre le carré de ![]() et un nombre réel
et un nombre réel ![]() à savoir :
à savoir :
![]()
Il faut donc discuter selon le signe de ![]() ce qui va conduire à distinguer (discriminer …) trois cas, selon que
ce qui va conduire à distinguer (discriminer …) trois cas, selon que ![]() est strictement positif, nul ou strictement négatif.
est strictement positif, nul ou strictement négatif.
Mais vu que ![]() tout repose en fait sur les épaules de
tout repose en fait sur les épaules de ![]() qu’on appelle donc, tout naturellement, le discriminant de l’équation
qu’on appelle donc, tout naturellement, le discriminant de l’équation ![]()
![]() Le membre de gauche de
Le membre de gauche de ![]() est une différence de deux carrés. On factorise et l’on trouve l’équation équivalente :
est une différence de deux carrés. On factorise et l’on trouve l’équation équivalente :
![Rendered by QuickLaTeX.com \[\left(x+\frac{b-\sqrt{\Delta}}{2a}\right)\left(x+\frac{b+\sqrt{\Delta}}{2a}\right)=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8104b114d83d13d15db5bfd5270fdbd6_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{S_{a,b,c}=\left\{ \frac{-b+\sqrt{\Delta}}{2a},\thinspace\frac{-b-\sqrt{\Delta}}{2a}\right\} }\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c695944535ef7dab527439a3c733fb64_l3.png)
![]() L’équation
L’équation ![]() se réduit à :
se réduit à :
![]()
![Rendered by QuickLaTeX.com \[\boxed{S_{a,b,c}=\left\{ -\frac{b}{2a}\right\} }\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-aea2c4522c0c42c6f4ba9afc5da9eba9_l3.png)
![]() On observe que, pour tout
On observe que, pour tout ![]() :
:
![]()
![]()
Donnons, pour clore cette section, un exemple pour chacun des trois cas :
Exemple 1 avec 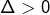
Résolution de
![]()
Le discriminant est ![]() Les solutions sont donc :
Les solutions sont donc :
![]()
Exemple 2 avec 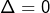
Résolution de
![]()
Le discriminant est ![]() L’unique solution est :
L’unique solution est :
![]()
Exemple 3 avec 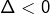
Résolution de
![]()
Le discriminant est ![]()
Cette équation ne possède aucune solution réelle.
Remarque
L’usage du discriminant réduit simplifie (très légèrement) la résolution de l’équation
![]()
![]()
Si ![]() les solutions sont données par les formules :
les solutions sont données par les formules :
![Rendered by QuickLaTeX.com \[\boxed{\frac{-b'\pm\sqrt{\Delta'}}{a}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2ca491db704bfdc526738c670733a307_l3.png)
Ainsi, dans l’exemple 3 ci-dessus, on pouvait écrire :
![]()
3 – Second degré en mode furtif
Il arrive que le processus de résolution conduise, après quelques manipulations, à une équation du second degré. Sans prétendre à l’exhaustivité, examinons (sur des exemples) quelques uns des principaux scénarios …
Exemple 1 – Avec des fractions
On demande de résoudre :
![Rendered by QuickLaTeX.com \[\boxed{\frac{1}{x}+\frac{1}{x+1}+\frac{1}{x+2}=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5a92cf9d1ed49735a62fc8dfeeba4c91_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{S=\left\{ -1-\frac{\sqrt{3}}{3},\thinspace-1+\frac{\sqrt{3}}{3}\right\} }\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6918f72241aa1aadb11fe95e5f46f4e4_l3.png)
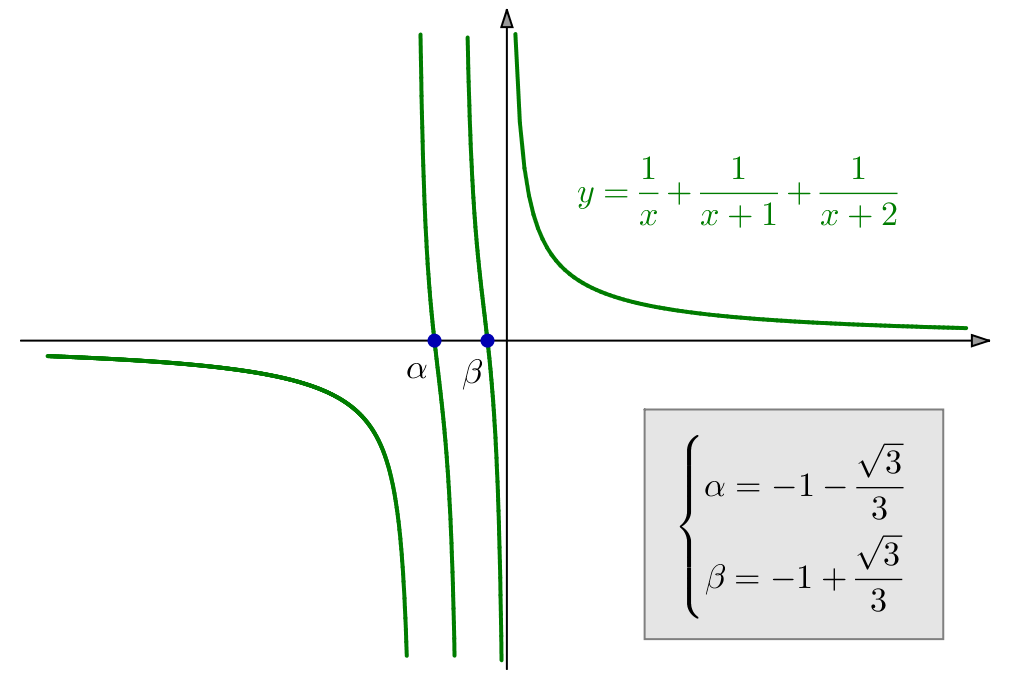
Exemple 2 – Encore des fractions
On demande de résoudre :
![Rendered by QuickLaTeX.com \[\boxed{\frac{x}{x^{2}-1}+\frac{1}{x}=\frac{7}{6}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-25520912ef57062a4f6fe66583df459b_l3.png)
Pour tout ![]() l’équation proposée équivaut à :
l’équation proposée équivaut à :
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{S=\left\{ \frac{-1-\sqrt{22}}{7},\thinspace\frac{-1+\sqrt{22}}{7},\thinspace2\right\} }\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0244aa530c040b9d3d241e3b1505cbe4_l3.png)
Noter le choix « avantageux » de la constante au second membre de l’équation.
Avec une autre valeur (par exemple 1 au lieu de ![]() on déboucherait en général sur une équation du troisième degré dont la résolution ne serait pas élémentaire (et nécessiterait l’usage des formules de Cardan).
on déboucherait en général sur une équation du troisième degré dont la résolution ne serait pas élémentaire (et nécessiterait l’usage des formules de Cardan).
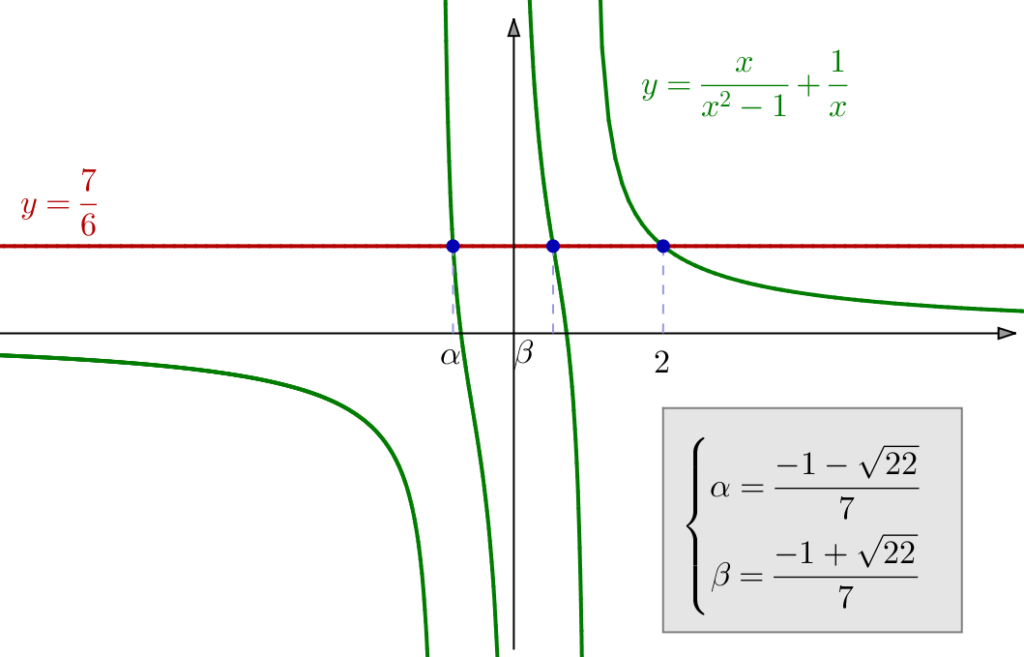
Exemple 3 – Avec des racines carrées
On demande de résoudre :
![]()
Pour tout ![]() les deux membres sont clairement positifs et l’on obtient une équation équivalente en élevant chacun au carré :
les deux membres sont clairement positifs et l’on obtient une équation équivalente en élevant chacun au carré :
![]()
![]()
Si ![]() le membre de droite est strictement négatif et ne peut donc pas être égal au membre de gauche.
le membre de droite est strictement négatif et ne peut donc pas être égal au membre de gauche.
Et si ![]() alors l’équation équivaut à :
alors l’équation équivaut à :
![]()
![]()
Son discriminant réduit est :
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{S=\left\{ \frac{78+12\sqrt{11}}{25}\right\} }\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9f97cb764f08a2ace80dc65efb9ffe4e_l3.png)
Exemple 4 – Avec des valeurs absolues
On demande de résoudre :
![]()
Il est naturel de distinguer trois cas, selon les signes des expressions ![]() et
et ![]()
![]() Pour
Pour ![]() l’équation s’écrit
l’équation s’écrit ![]() c’est-à-dire
c’est-à-dire ![]() ou encore
ou encore ![]()
Mais les réels ![]() et
et ![]() ne vérifient pas la condition
ne vérifient pas la condition ![]() et ne sont donc pas retenus.
et ne sont donc pas retenus.
![]() Pour
Pour ![]() on résout
on résout ![]() c’est-à-dire
c’est-à-dire ![]() Parmi les deux solutions de cette équation du second degré, seule
Parmi les deux solutions de cette équation du second degré, seule ![]() est retenue.
est retenue.
![]() Enfin, pour
Enfin, pour ![]() l’équation prend la forme
l’équation prend la forme ![]() c’est-à-dire
c’est-à-dire ![]() : seule la solution
: seule la solution ![]() est retenue.
est retenue.
Finalement :
![]()
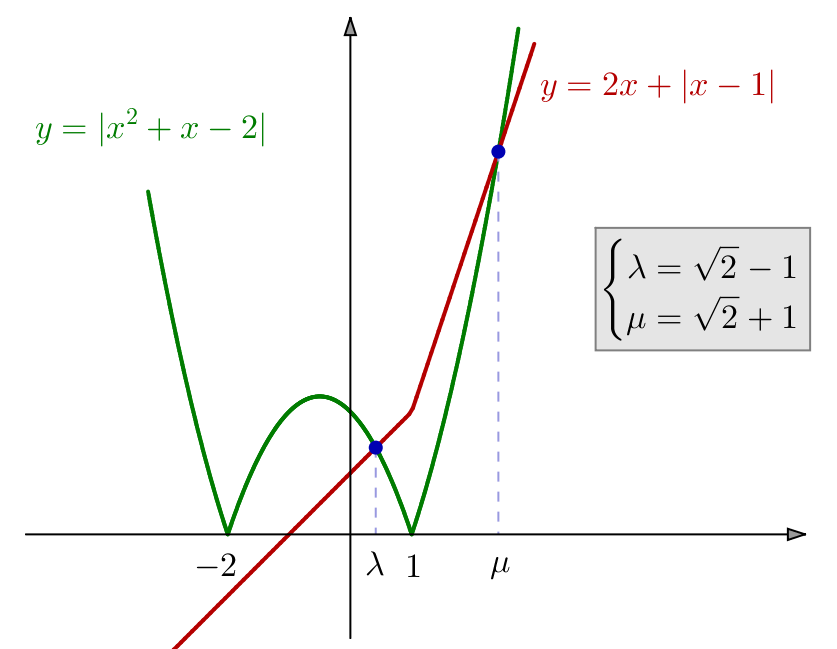
Exemple 5 – Avec une racine carrée et une valeur absolue
On demande de résoudre :
![]()
Si
Et pour ![]() l’équation proposée équivaut à :
l’équation proposée équivaut à :
![]()
![]()
![]()
Alors l’équation prend la forme :
![]()
![]()
![]()
![]()
![]()
![]()
Cette fois, l’équation équivaut à :
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{\mathcal{S}=\left\{ \frac{3-3\sqrt{17}}{8},\thinspace-\frac{3}{5},\thinspace0,\thinspace\frac{3+3\sqrt{17}}{8}\right\} }\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-908e2af8f95c36fa9543a8882c4c855a_l3.png)
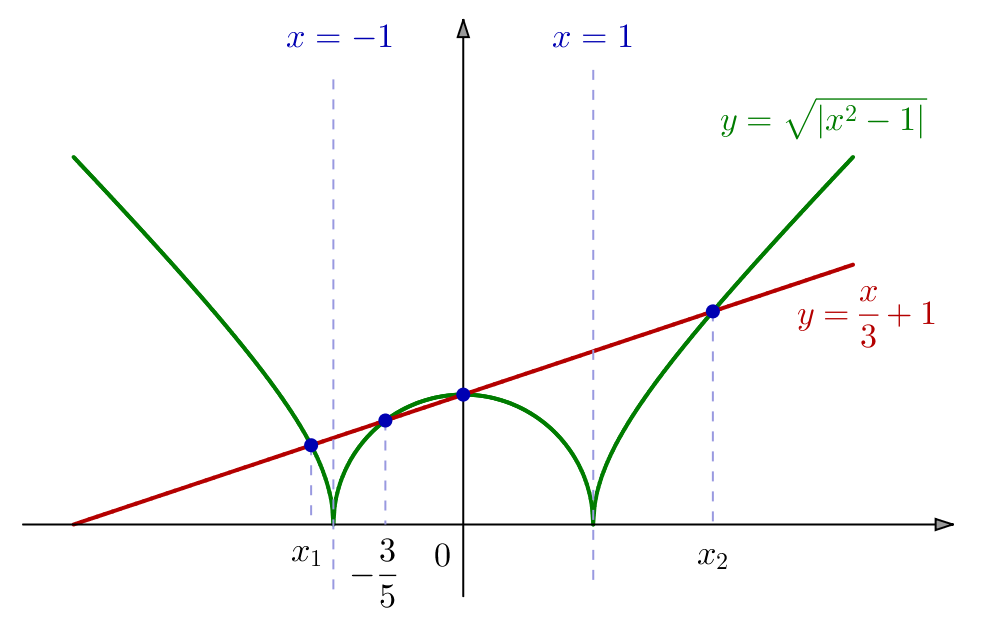
Exemple 6 – Avec un changement d’inconnue
On demande de résoudre :
(![]() )
) ![]()
Au fait … qu’est-ce qu’une équation algébrique ? [cliquer pour déplier]
Il convient de préciser ce point de vocabulaire. On désigne ainsi les équations de la forme ![]() , où
, où ![]() est un polynôme. Autrement dit, une équation est dite algébrique lorsqu’elle est de la forme :
est un polynôme. Autrement dit, une équation est dite algébrique lorsqu’elle est de la forme :
(![]() )
) ![]()
les symboles ![]() désignant des réels fixés, appelés coefficients de l’équation.
désignant des réels fixés, appelés coefficients de l’équation.
De manière générale, une équation algébrique de la forme ![]() est dite de degré
est dite de degré ![]() à condition toutefois que la coefficient
à condition toutefois que la coefficient ![]() soit non nul.
soit non nul.
Les équations du second degré sont donc des équations algébriques particulières : elles correspondent à ![]() dans la définition ci-dessus.
dans la définition ci-dessus.
L’équation suivante est algébrique de degré 7 :
![]()
Une équation qui n’est équivalente à aucune équation algébrique est dite transcendante. C’est par exemple le cas de l’équation ![]()
En regardant l’équation ![]() de plus près, on constate que les exposants auxquels figure l’inconnue
de plus près, on constate que les exposants auxquels figure l’inconnue ![]() sont tous pairs.
sont tous pairs.
Ceci suggère de changer temporairement de cible et de poser ![]() ce qui nous conduit à considérer l’équation auxiliaire :
ce qui nous conduit à considérer l’équation auxiliaire :
(![]() )
) ![]()
![]()
Les calculs précédents montrent que, pour tout ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[\boxed{S=\left\{ -\sqrt{2},-1,-\frac{1}{2},\frac{1}{2},1,\sqrt{2}\right\} }\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-dbafa967dcd56926aaaf00a82145440c_l3.png)
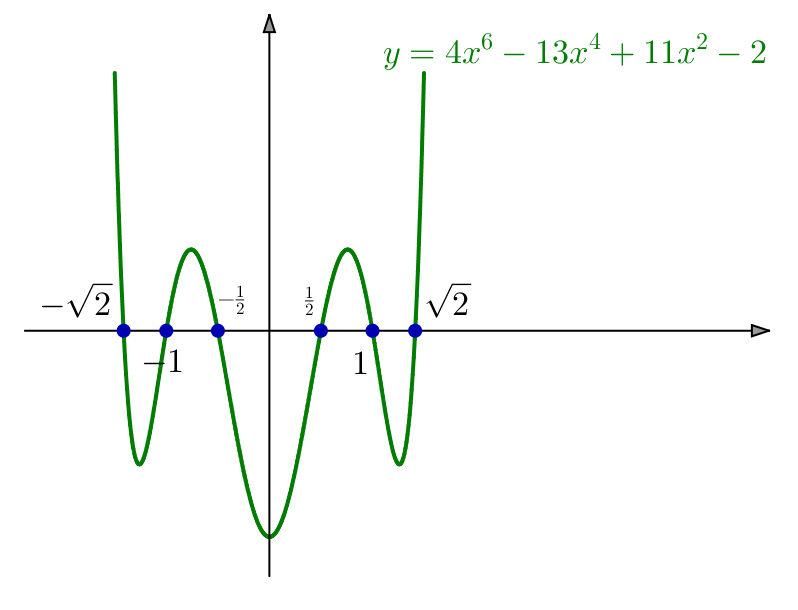
Exemple 7 – Un changement d’inconnue plus élaboré
Dans l’exemple précédent, l’ensemble de solutions de l’équation proposée était invariant par la transformation ![]() ce qui veut simplement dire que l’opposé de toute solution était encore solution.
ce qui veut simplement dire que l’opposé de toute solution était encore solution.
Les équations algébriques ayant cette propriété sont aisément reconnaissables : ce sont celles dans lesquelles l’inconnue figure à des exposants qui sont tous de même parité (cette formulation peut être rendue rigoureuse, mais on s’en contentera).
Les équations algébriques ne possédant pas 0 pour solution et pour lesquels l’inverse de toute solution est encore solution sont appelées équations réciproques.
On les reconnaît facilement : la liste des coefficients forme un palindrome.
Un palindrome est une liste de symboles qui reste inchangée lorsqu’on la renverse. Par exemple, la liste des chiffres de l’entier ![]() ou bien la liste des lettres du mot « radar », etc …
ou bien la liste des lettres du mot « radar », etc …
Pas clair ? Considérons l’équation algébrique :
![]()
![]()
Alors, il est possible traiter ce genre d’équations avec le changement d’inconnue :
![Rendered by QuickLaTeX.com \[\boxed{y=x+\frac{1}{x}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fa2667564ab66826f278301d1a10d08b_l3.png)
On constate cette que égalité impose :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{S=\left\{ \frac{-9-\sqrt{65}}{4},\thinspace\frac{-9+\sqrt{65}}{4},\thinspace\frac{1}{2},\thinspace2\right\} }\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-557c740a380fd46ec7f183002dd3bd50_l3.png)
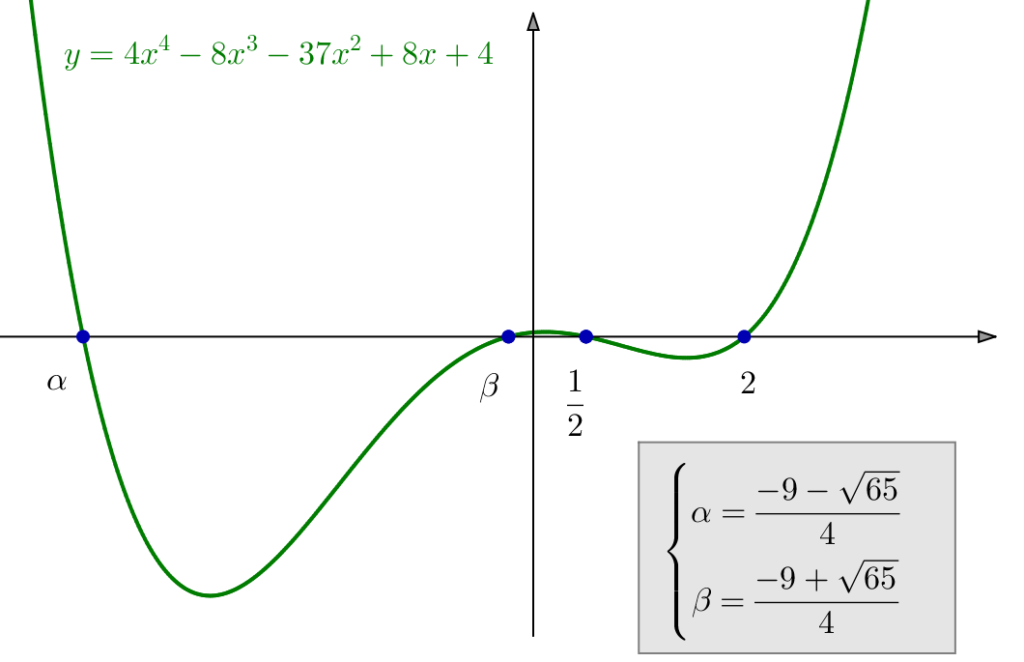
Afin qu’on puisse y voir quelque chose, les unités ne sont pas identiques sur chacun des axes de coordonnées : le tracé a subi une compression d’un facteur 100 en ordonnées. Pour le dire autrement, on a tracé en axes orthonormés le graphe de ![]()
4 – Résolution explicite impossible
La résolution des équations algébriques est maîtrisée depuis fort longtemps pour ce qui concerne le second degré, comme en attestent des inscriptions cunéiformes retrouvées sur des tablettes d’argile datant de près de 4000 ans et remontant à l’époque babylonienne.
C’est à l’école mathématique italienne de la renaissance (XVIème siècle) que l’on doit la mise au point de techniques de résolutions des équations des 3ème et 4ème degrés avec, au passage, l’invention (ou la découverte ?) de ce qu’on devait plus tard appeler les nombres complexes.
Les travaux de J.L. Lagrange, suivis au début du XIX-ème siècle par ceux de N.H. Abel et E. Galois, devaient enfin aboutir à une connaissance complète du sujet et parvenir notamment au résultat suivant, à la fois profond et surprenant :
Théorème (délibérément non formalisé)
Il n’est pas possible d’exprimer en toute généralité les solutions des équations algébriques de degré 5 ou plus, en fonction des coefficients de celles-ci, par des formules utilisant seulement les quatre opérations usuelles (addition, soustraction, multiplication et division) ainsi que les extractions de racines (carrées, cubiques, etc …).
Cela ne signifie pas qu’il s’agisse de formules difficiles d’accès et que personne ne soit encore parvenu à les trouver … Le message est clair et définitif : de telles formules n’existent pas !
Bien sûr, on parle ici de formules générales : rien n’interdit de tomber, ici ou là, sur une équation algébrique de degré 5 (ou plus) que l’on sache résoudre explicitement.
Pour en savoir davantage sur ce sujet passionnant, je recommande vivement cet article écrit par le mathématicien Arnaud Beauville. Il comporte quatre chapitre : le premier nous concerne plus spécialement puisqu’il aborde l’histoire des équations du second degré; mais les trois suivants, quoique moins faciles d’accès, sont tout aussi passionnants. A noter aussi, du même auteur, cette présentation à lire en plein écran avec une visionneuse PDF (comme Acrobat Reader
par exemple). On peut aussi consulter cette vidéo, dans laquelle Arnaud Beauville nous raconte cette histoire en une cinquantaine de minutes.
Bref, il faut se résigner : la résolution d’une équation algébrique de degré supérieur ou égal à 5 n’est pas envisageable, au sens où on l’entend habituellement (voir l’encadré ci-dessus). Mais on peut néanmoins trouver des valeurs approchées, aussi précises qu’on le souhaite, pour les solutions.
Je propose de conclure cet article en examinant l’équation :
(![]() )
) ![]()
![]()
On observe en outre que ![]() et que
et que ![]() ce qui prouve que
ce qui prouve que ![]()
Le moyen le plus élémentaire améliorer cet encadrement est la méthode de dichotomie.
Elle consiste à construire une couple de suites réelles ![]() et
et ![]() de la manière suivante :
de la manière suivante :
D’une part :
![]()
![]() si
si ![]() et
et ![]() sont de signes contraires, alors :
sont de signes contraires, alors :
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{ccc}a_{n+1} & = & a_{n}\\\\b_{n+1} & = & \frac{a_{n}+b_{n}}{2}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-074fa4bed6f5d62cd3b6167669b95140_l3.png)
![]() et sinon :
et sinon :
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{ccc}a_{n+1} & = & \frac{a_{n}+b_{n}}{2}\\\\b_{n+1} & = & b_{n}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d9d6c353fa8818a3797deae30542bb9e_l3.png)
Les quelques lignes de code ci-dessous, écrites en Python, permettent le calcul d’une valeur approchée de ![]() avec une précision arbitraire. Vous n’aurez aucun mal à les adapter au cas d’une autre équation.
avec une précision arbitraire. Vous n’aurez aucun mal à les adapter au cas d’une autre équation.
from fractions import Fraction as fr
def f(x):
x2 = x * x
x4 = x2 * x2
return x * x4 + 2 * x - 1
def dichot(a, b, e):
u = a
v = b
while v - u > e:
m = (u + v) / 2
if f(m) >= 0:
v = m
else:
u = m
return (u,v)La fonction dichot, invoquée avec les arguments 0, 1 et 1e-7 renvoie les bornes d’un encadrement d’amplitude ![]() pour
pour ![]() .
.
L’import du module fractions autorise la manipulation de rationnels (plutôt que de nombres à virgule flottante), ce qui élimine non seulement les erreurs d’arrondis mais permet aussi d’atteindre une précision arbitraire.
dichot (0,1,1e-7)(0.4863889813423157, 0.48638904094696045)
>>> dichot(fr(0,1), fr(1,1), fr(1,10000000))Fraction(8160253,16777216),Fraction(4080127,8388608))
Le résultat de la première évaluation signifie que :
![]()
![]()
![]()
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.




Bonjour Monsieur,
Lorsque vous évoquez Messieurs Lagrange, Abel et Galois avant le théorème de fin d’article, une barre I s’est perdue entre les deux X pour évoquer le 19-ème siècle (ou alors vous testez la culture historique de certains de vos élèves qui seraient ici 🙂 ) !
Bien à vous.
Encore une coquille débusquée grâce à votre lecture attentive ! Merci 🙂