
Cet article présente quelques unes des principales techniques pour étudier les variations d’une fonction numérique et obtenir ensuite un tracé suffisamment précis de son graphe.
Les exemples proposés sont de difficulté variée. La plupart sont accessibles dès la terminale. Quelques uns sont plus élaborés et requièrent davantage de connaissances.
Dans tout ce qui suit, ![]() désigne une fonction numérique, c’est-à-dire une fonction
désigne une fonction numérique, c’est-à-dire une fonction ![]() de
de ![]() dans
dans ![]() .
.
1 – Domaine de définition
On démarre l’étude de ![]() en déterminant les réels
en déterminant les réels ![]() pour lesquels l’expression
pour lesquels l’expression ![]() est bien définie. L’ensemble de ces valeurs est appelé le domaine de définition de
est bien définie. L’ensemble de ces valeurs est appelé le domaine de définition de ![]() On peut le noter
On peut le noter ![]()
Par exemple, le calcul de :
![]()
![Rendered by QuickLaTeX.com \[\boxed{D_{f}=\left[-1,\frac{1}{3}\right[\cup\left]\frac{1}{3},1\right]}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-73825c3a1f9dc9b36d35833020a15e77_l3.png)
Et pour que l’expression :
![]()
![]()
![]()
Exercice 1
Vous pouvez vous entraîner en déterminant les domaines de définition des fonctions suivantes :
![Rendered by QuickLaTeX.com \[\begin{array}{ccc}f\left(x\right)={\displaystyle \frac{x-1}{x^{2}-4}} & ; & g\left(x\right)={\displaystyle \frac{1}{x-\frac{1}{x}}}\\ \\h\left(x\right)={\displaystyle \frac{\sqrt{x}}{1+\sqrt{x}}} & ; & u\left(x\right)={\displaystyle \frac{x^{2}-2x+1}{\left(x-1\right)^{2}}}\\ \\v\left(x\right)={\displaystyle \sqrt{x}-\frac{1}{\sqrt{1-x}}} & ; & w\left(x\right)={\displaystyle \frac{x-1-\sqrt{-x}}{x^{2}-x}}\end{array}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-28bb0e69982719d1926cc512d02d2681_l3.png)
![Rendered by QuickLaTeX.com \[\begin{array}{ccc}F\left(x\right)={\displaystyle \ln\left(\frac{x^{2}-1}{x}\right)} & ; & G\left(x\right)={\displaystyle \frac{\ln\left(x\right)}{\sqrt{1+\ln\left(x\right)}}}\\ \\H\left(x\right)={\displaystyle \frac{x}{e^{x}-1-x}} & ; & U\left(x\right)={\displaystyle \frac{\ln\left(\ln\left(x\right)\right)}{\ln\left(x\right)-2}}\\ \\V\left(x\right)=\ln\left(\sin\left(x\right)\right) & ; & W\left(x\right)={\displaystyle \frac{\sin\left(x\right)}{\cos^{2}\left(x\right)+\left(2x-\pi\right)^{2}}}\end{array}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-80cac1fc41bbaaecb6e07042707f6efd_l3.png)
2 – Eventuelles symétries
Le graphe de ![]() est par définition :
est par définition :
![]()
Ce graphe peut parfois présenter des symétries. En les détectant à l’avance, on limite l’étude de ![]() à une partie de
à une partie de ![]() On trace alors une portion du graphe, que l’on complète ensuite pour obtenir le graphe entier, en utilisant la (ou les) symétrie(s) en question.
On trace alors une portion du graphe, que l’on complète ensuite pour obtenir le graphe entier, en utilisant la (ou les) symétrie(s) en question.
Les deux symétries les plus simples, auxquelles nous nous limiterons, sont les suivantes :
- symétrie par rapport à une droite « verticale » d’équation
 pour un certain
pour un certain 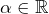
- symétrie centrale par rapport à un point
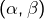
Formalisons cette histoire de symétrie.
Définition
Soit ![]() On dit que
On dit que ![]() est symétrique par rapport à
est symétrique par rapport à ![]() lorsque :
lorsque :
![]()
Noter que ![]() peut ne pas appartenir à
peut ne pas appartenir à ![]() Par exemple :
Par exemple : ![]() est symétrique par rapport à 0.
est symétrique par rapport à 0.
On peut alors établir la :
Proposition
Soit ![]() une partie de
une partie de ![]() symétrique par rapport à
symétrique par rapport à ![]() et soit
et soit ![]() une application.
une application.
On note ![]() le graphe de
le graphe de ![]() .
.
- Si :
alors![Rendered by QuickLaTeX.com \[\forall x\in A,\thinspace f\left(x\right)=f\left(2\alpha-x\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-38094bedbedd9c8ecb2b0c415e877e06_l3.png)
 présente une symétrie par rapport à la droite d’équation
présente une symétrie par rapport à la droite d’équation 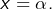
- S’il existe
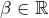 tel que :
tel que :
alors![Rendered by QuickLaTeX.com \[\forall x\in A,\thinspace f\left(x\right)+f\left(2\alpha-x\right)=2\beta\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-771d9851f2ed610a1d633ab6cfb749f5_l3.png)
 présente une symétrie centrale de centre
présente une symétrie centrale de centre 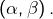
Donnons deux exemples; un pour chacun des deux scénarios …
Exemple 1
Considérons la fonction ![]() définie par :
définie par :
![]()
![]()
Tout d’abord, modifions l’écriture de ![]() en remarquant que :
en remarquant que :
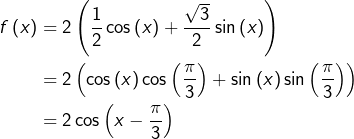
On voit maintenant que :
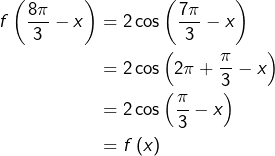
d’équation
Précisons que cette droite n’est pas le seul axe de symétrie ! Pour tout ![]() la droite d’équation
la droite d’équation ![]() est axe de symétrie.
est axe de symétrie.
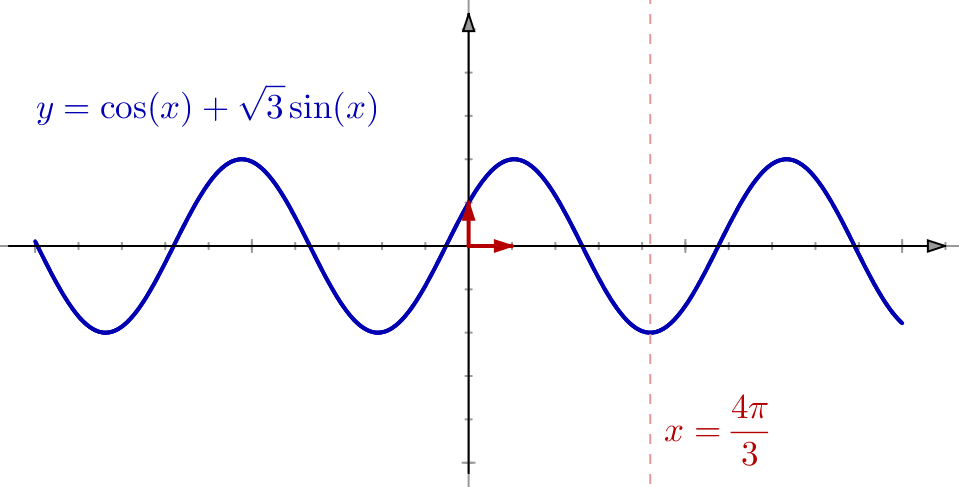
Exemple 2
Considérons la fonction ![]() définie par :
définie par :
![Rendered by QuickLaTeX.com \[\boxed{\forall x\in\mathbb{R},\thinspace g\left(x\right)=\frac{e^{x}}{e^{x}+1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c104fe5b8f2143ca4ef624b2aeca1090_l3.png)
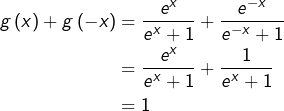
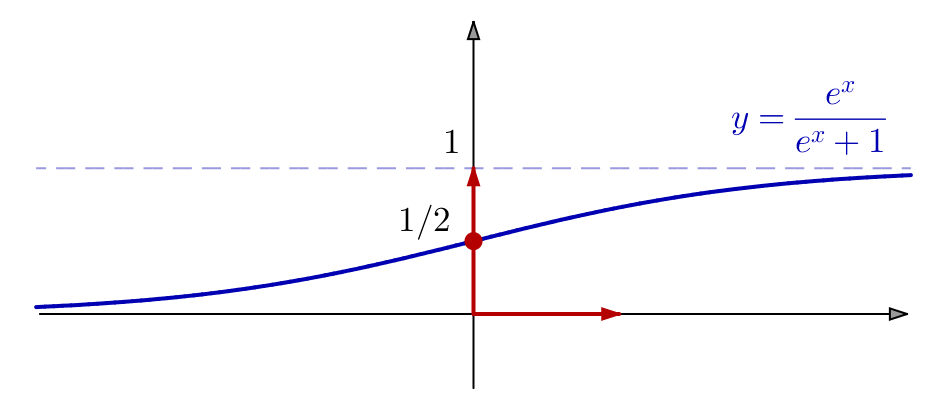
Ce point ![]() est aussi l’unique point d’inflexion du graphe de
est aussi l’unique point d’inflexion du graphe de ![]() (voir section 5).
(voir section 5).
Exercice 2
1°) Vérifier que la courbe d’équation
![]()
2°) Vérifier que la courbe d’équation
![]()
3 – Périodicité éventuelle
Définition
Une partie ![]() de
de ![]() est dite invariante par translation de
est dite invariante par translation de ![]() (pour un certain réel
(pour un certain réel ![]() lorsque :
lorsque :
![]()
Par exemple, ![]() est invariant par translation de 1.
est invariant par translation de 1.
On notera que si ![]() est invariant par translation de
est invariant par translation de ![]() alors
alors ![]() est aussi invariant par translation de
est aussi invariant par translation de ![]() quel que soit l’entier
quel que soit l’entier ![]()
Exercice 3
Sauriez-vous prouver que si ![]() est invariant par translation de
est invariant par translation de ![]() alors il en va de même pour
alors il en va de même pour ![]() ?
?
Exercice 4
On note ![]() . Montrer qu’il existe des nombres réels
. Montrer qu’il existe des nombres réels ![]() arbitrairement petits tels que
arbitrairement petits tels que ![]() soit invariant par translation de
soit invariant par translation de ![]()
Nous pouvons maintenant définir la notion de fonction périodique.
Définition
Etant donné ![]() et une partie
et une partie ![]() de
de ![]() invariante par translation de
invariante par translation de ![]() une application
une application ![]() est dite T-périodique lorsque :
est dite T-périodique lorsque :
![]()
Noter qu’on a alors :
![]()
![]()
Lorsqu’une fonction est ![]() périodique, son graphe est invariant par translation de vecteur
périodique, son graphe est invariant par translation de vecteur ![]() (et aussi de vecteur
(et aussi de vecteur ![]() et, plus généralement, de vecteur
et, plus généralement, de vecteur ![]() pour tout entier
pour tout entier ![]()
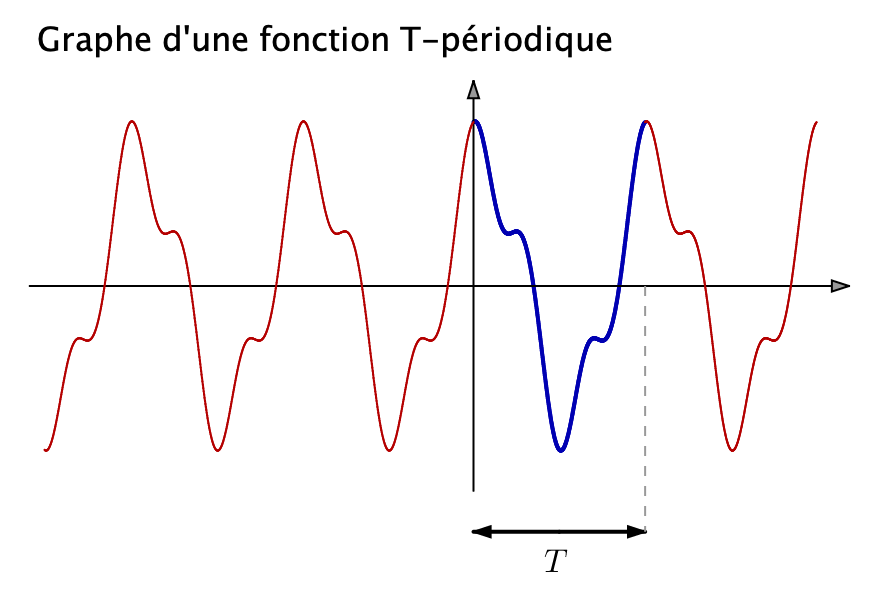
Trois exemples classiques de fonctions périodiques :
- L’application
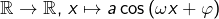 est
est 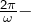 périodique (
périodique (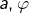 deux réels donnés).
deux réels donnés). - L’application
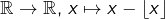 est
est 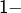 périodique.
périodique. - Si l’on pose
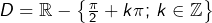 , alors l’application
, alors l’application 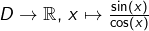 (appelée fonction tangente) est
(appelée fonction tangente) est  périodique.
périodique.
Illustration dynamique
Graphe de ![]()
En jouant avec les sliders, on modifie ![]() (l’amplitude) ,
(l’amplitude) , ![]() (la pulsation) et
(la pulsation) et ![]() (le déphasage). Les touches P (plus) et M (moins) permettent de (dé-)zoomer. Le système de coordonnées peut être translaté en cliquant-déplaçant dans la zone d’affichage.
(le déphasage). Les touches P (plus) et M (moins) permettent de (dé-)zoomer. Le système de coordonnées peut être translaté en cliquant-déplaçant dans la zone d’affichage.
Exercice 5
Si ![]() sont périodiques, peut-on affirmer que
sont périodiques, peut-on affirmer que ![]() est aussi périodique ?
est aussi périodique ?
4 – Rôle de la dérivée
On s’intéresse maintenant au sens de variation d’une fonction.
Commençons par préciser le vocabulaire :
Définition
Soit ![]() une partie de
une partie de ![]() et soit
et soit ![]() une application.
une application.
➡ ![]() est dite croissante lorsque :
est dite croissante lorsque :
![]() pour tout couple
pour tout couple ![]() tel que
tel que ![]()
➡ ![]() est dite strictement croissante lorsque :
est dite strictement croissante lorsque :
![]() pour tout couple
pour tout couple ![]() tel que
tel que ![]()
Définitions analogues pour « décroissante » et « strictement décroissante ».
Enfin, ![]() est dite (strictement) monotone si elle est (strictement) croissante ou (strictement) décroissante.
est dite (strictement) monotone si elle est (strictement) croissante ou (strictement) décroissante.
Attention !! Une erreur classique consiste à affirmer que si ![]() vérifie
vérifie
![]()
Preuve (cliquer pour déplier / replier)
Considérons, pour tout ![]() l’application :
l’application :
![]()
![]()
Supposons ![]() Alors :
Alors :
![Rendered by QuickLaTeX.com \[\left\{\begin{array}{c}f_{\omega}'\left(0\right)=1+\omega>0\\\\f_{\omega}'\left(\frac{\pi}{\omega}\right)=1-\omega<0\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9a04a9ba483320b08a7cbd4d5274c2a4_l3.png)
Par continuité de ![]() on en déduit qu’il existe :
on en déduit qu’il existe :
- un intervalle
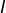 centré en 0 tel que
centré en 0 tel que 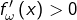 pour tout
pour tout 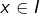
- un intervalle
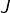 centré en
centré en 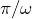 tel que
tel que 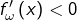 pour tout
pour tout 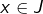
Par conséquent, ![]() est strictement croissante sur
est strictement croissante sur ![]() , strictement décroissante sur
, strictement décroissante sur ![]() et donc pas monotone (sur
et donc pas monotone (sur ![]() . Dans le même temps, on observe que :
. Dans le même temps, on observe que :
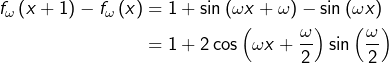
![]()
![]()
Le résultat suivant est fondamental :
Théorème
Soit ![]() un intervalle non trivial
un intervalle non trivial ![]() et soit
et soit ![]() une application dérivable.
une application dérivable.
- Si
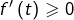 pour tout
pour tout 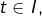 alors
alors  est croissante.
est croissante. - Si
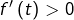 pour tout
pour tout 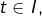 alors
alors  est strictement croissante.
est strictement croissante.
Bien entendu, si ![]() pour tout
pour tout ![]() alors
alors ![]() est décroissante. Il suffit d’appliquer le premier point du théorème à
est décroissante. Il suffit d’appliquer le premier point du théorème à ![]() .
.
De même, si ![]() pour tout
pour tout ![]() alors
alors ![]() est strictement décroissante.
est strictement décroissante.
On prouve ce théorème grâce à la formule des accroissements finis :
Soient ![]() tels que
tels que ![]() D’après la formule des accroissements finis :
D’après la formule des accroissements finis :
![]()
Et de même, sous l’hypothèse ![]() on voit que
on voit que ![]() ce qui montre la stricte croissance de
ce qui montre la stricte croissance de ![]()
Ajoutons quelques observations :
- L’hypothèse que
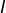 est un intervalle n’est pas superflue ! Par exemple, l’application
est un intervalle n’est pas superflue ! Par exemple, l’application
possède une dérivée strictement négative en tout point, mais n’est pas monotone. En effet : d’une part![Rendered by QuickLaTeX.com \[\Phi:\mathbb{R}^{\star}\rightarrow\mathbb{R},\thinspace x\mapsto\frac{1}{x}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-23abec6ad379b57d4a8dd07723ec0e30_l3.png)
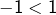 et
et  donc
donc  n’est pas décroissante et, d’autre part
n’est pas décroissante et, d’autre part 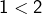 et
et  donc
donc  n’est pas croissante. Bien entendu, la restriction de
n’est pas croissante. Bien entendu, la restriction de  à chacun des intervalles
à chacun des intervalles ![Rendered by QuickLaTeX.com \left]-\infty,0\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-96cffb96d97afa19bd62834dd5bc71a5_l3.png) et
et ![Rendered by QuickLaTeX.com \left]0,+\infty\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-90d2d03eec9a031b0d2601b2f615f2df_l3.png) est strictement décroissante.
est strictement décroissante. - La réciproque de
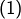 est vraie (mais nettement moins utile) : si
est vraie (mais nettement moins utile) : si  est croissante alors
est croissante alors 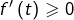 pour tout
pour tout 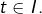
- La réciproque de
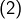 est fausse. Autrement dit,
est fausse. Autrement dit,  peut être strictement croissante même si
peut être strictement croissante même si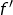 s’annule. Par exemple, l’application
s’annule. Par exemple, l’application 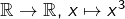 est strictement croissante bien que sa dérivée s’annule en
est strictement croissante bien que sa dérivée s’annule en 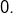 Afin de préciser cette remarque, on peut énoncer le :
Afin de préciser cette remarque, on peut énoncer le :
Théorème
Soit ![]() un intervalle non trivial
un intervalle non trivial ![]() et soit
et soit ![]() une application dérivable. Alors, les assertions suivantes sont équivalentes :
une application dérivable. Alors, les assertions suivantes sont équivalentes :
 est strictement croissante
est strictement croissante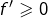 et l’ensemble
et l’ensemble 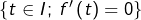 est d’intérieur vide
est d’intérieur vide
En particulier, il suffit que ![]() soit positive et ne s’annule qu’en un nombre fini de points pour que
soit positive et ne s’annule qu’en un nombre fini de points pour que ![]() soit strictement croissante.
soit strictement croissante.
Exercice 6
Donner un exemple d’une application ![]() dérivable, strictement croissante et dont la dérivée s’annule une infinité de fois.
dérivable, strictement croissante et dont la dérivée s’annule une infinité de fois.
5 – Convexité
Considérons un intervalle non trivial ![]() et une application
et une application ![]()
Notons toujours ![]() le graphe de
le graphe de ![]()
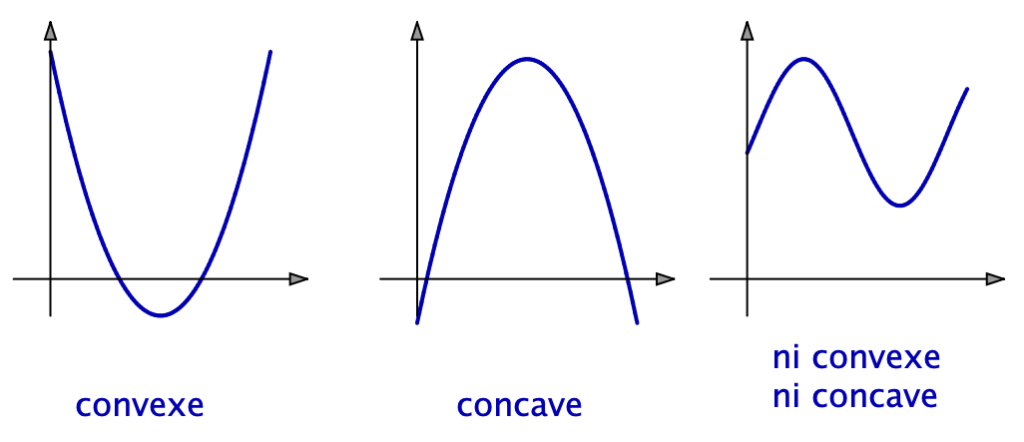
Naïvement parlant, ![]() est convexe lorsque
est convexe lorsque ![]() est « tourné vers le haut » et concave lorsque
est « tourné vers le haut » et concave lorsque ![]() est « tourné vers le bas ».
est « tourné vers le bas ».
Cela dit, une définition rigoureuse de la convexité s’impose. La voici :
Définition
L’application ![]() est dite convexe lorsque, pour tout couple
est dite convexe lorsque, pour tout couple ![]() d’éléments de
d’éléments de ![]() et pour tout
et pour tout ![]() :
:
![]()
Ajoutons que ![]() est dite concave lorsque
est dite concave lorsque ![]() est convexe, ce qui revient simplement à dire que le sens de l’inégalité est renversé.
est convexe, ce qui revient simplement à dire que le sens de l’inégalité est renversé.
Pour en savoir un peu plus, on pourra consulter cette rubrique du lexique Math-OS.
Dans cet article de niveau lycée, nous n’approfondirons pas davantage ce point de vue. L’accent est plutôt mis sur la :
Proposition
Etant donnée ![]() deux fois dérivable, les assertions suivantes sont équivalentes :
deux fois dérivable, les assertions suivantes sont équivalentes :
 est convexe
est convexe- pour tout
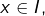
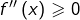
Comme on peut s’en douter, on a aussi : ![]() concave si et seulement si
concave si et seulement si ![]() pour tout
pour tout ![]() Il suffit d’appliquer la proposition ci-dessus à
Il suffit d’appliquer la proposition ci-dessus à ![]()
Lorsque la dérivée seconde de ![]() s’annule et change de signe pour
s’annule et change de signe pour ![]() le graphe
le graphe ![]() de
de ![]() change de concavité. On dit que
change de concavité. On dit que ![]() est un point d’inflexion pour
est un point d’inflexion pour ![]() Sur l’illustration ci-dessous, on en dénombre sept :
Sur l’illustration ci-dessous, on en dénombre sept :
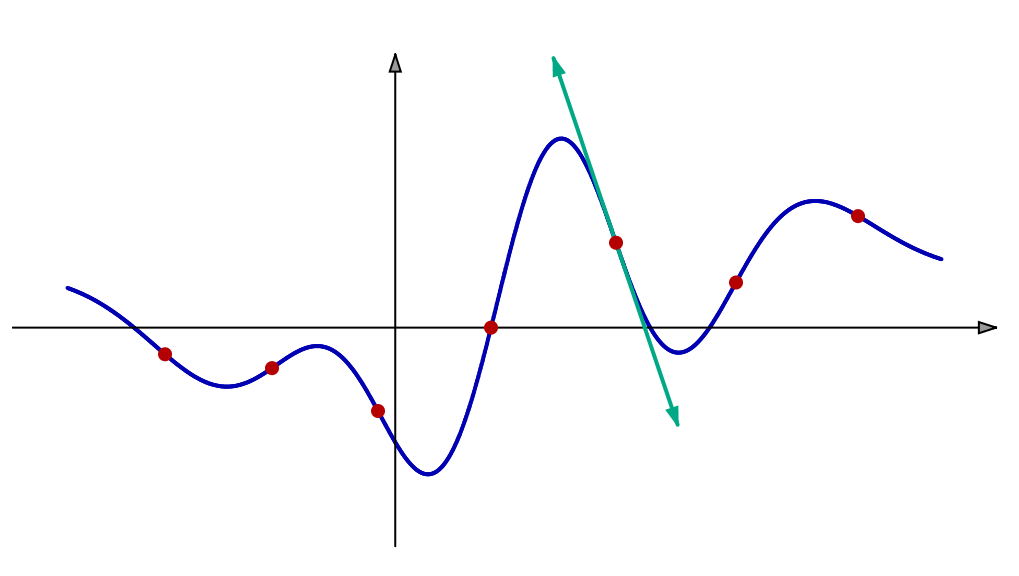
Comme on peut le voir, ![]() traverse localement sa tangente en un point d’inflexion.
traverse localement sa tangente en un point d’inflexion.
Exercice 7
Si ![]() sont convexes, peut-on affirmer que
sont convexes, peut-on affirmer que ![]() est aussi convexe ?
est aussi convexe ?
6 – Branches Infinies
Examinons l’application :
![Rendered by QuickLaTeX.com \[\boxed{g:\mathbb{R}\rightarrow\mathbb{R},\thinspace x\mapsto\frac{x^{3}+2x^{2}-2x-3}{x^{2}+1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1ad4a5b10f1bb2367ade1aad5b8867de_l3.png)
Lorsque ![]() est « très grand », on comprend intuitivement que la valeur de l’expression
est « très grand », on comprend intuitivement que la valeur de l’expression ![]() quoique certainement très élevée, ne fait pas le poids devant le terme
quoique certainement très élevée, ne fait pas le poids devant le terme ![]() considérablement plus grand.
considérablement plus grand.
Grosso modo, le numérateur se comporte comme ![]() lorsque
lorsque ![]() tend vers
tend vers ![]() De la même manière, le dénominateur se comporte comme
De la même manière, le dénominateur se comporte comme ![]() de sorte que
de sorte que ![]() doit se comporter comme
doit se comporter comme ![]()
A présent, rendons cela rigoureux …
En mettant le terme prépondérant en facteur, au numérateur comme au dénominateur, on peut écrire ![]() sous la forme :
sous la forme :
![Rendered by QuickLaTeX.com \[g\left(x\right) = \frac{x^{3}\left(1+\frac{2}{x}-\frac{2}{x^{2}}-\frac{3}{x^{3}}\right)}{x^{2}\left(1+\frac{1}{x^{2}}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3d2c0ad1121572d96ae42ad59bd0e8ae_l3.png)
![]()
On dit que ![]() équivaut à
équivaut à ![]() lorsque
lorsque ![]() tend vers
tend vers ![]() (pour exprimer que le quotient de ces deux quantités tend vers
(pour exprimer que le quotient de ces deux quantités tend vers ![]() ce qui se note :
ce qui se note :
![]()
Afin de préciser davantage le comportement de ![]() pour les grandes valeurs de
pour les grandes valeurs de ![]() on s’intéresse maintenant à la différence :
on s’intéresse maintenant à la différence :
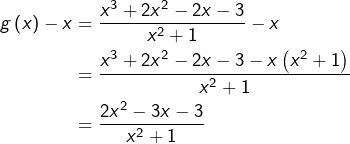
![]()
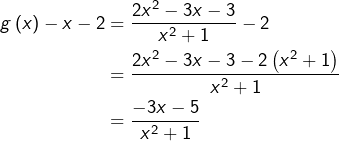
![]()
Il est temps de donner une :
Définition
Etant donnée une application ![]() s’il existe un couple
s’il existe un couple ![]() tel que :
tel que :
![]()
On dit que la droite ![]() d’équation
d’équation ![]() est asymptote au graphe
est asymptote au graphe ![]() de
de ![]() en
en ![]()
Si ![]() on dit que
on dit que ![]() est une asymptote oblique et l’on parle d’asymptote horizontale si
est une asymptote oblique et l’on parle d’asymptote horizontale si ![]()
Afin de préciser les positions relatives de ![]() et
et ![]()
(c’est-à-dire : « qui est au-dessus de qui »), on devra déterminer le signe de l’expression ![]()
Pour revenir à l’exemple de la fonction ![]() son graphe
son graphe ![]() présente en
présente en ![]() une asymptote oblique
une asymptote oblique ![]() d’équation
d’équation ![]()
En outre, le calcul a montré que la différence ![]() est du même signe que
est du même signe que ![]() c’est-à-dire positif si
c’est-à-dire positif si ![]() et négatif sinon. Ceci donne les positions relatives de
et négatif sinon. Ceci donne les positions relatives de ![]() et
et ![]() :
:
- pour
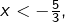
 est au-dessus de
est au-dessus de 
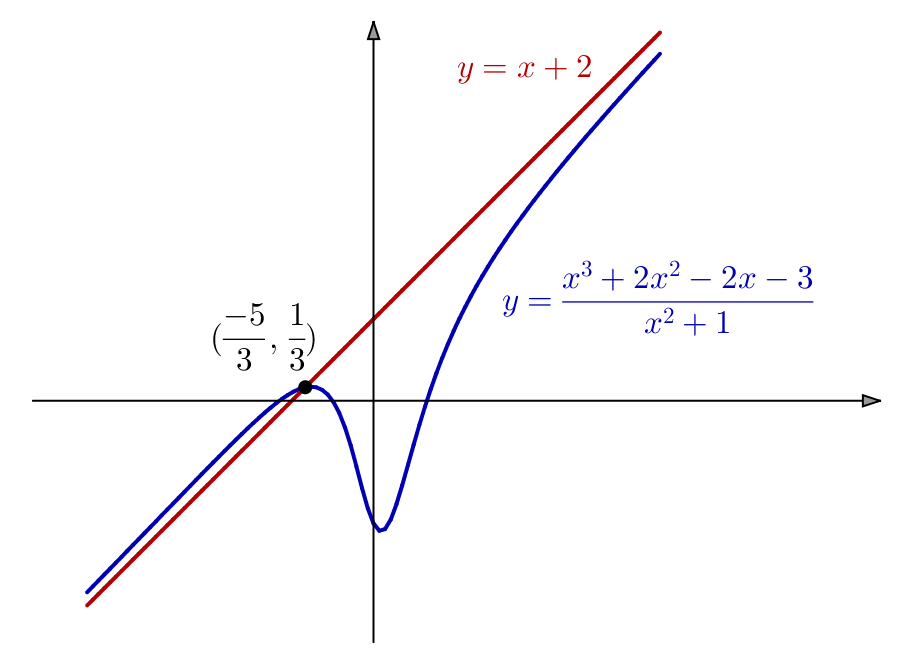
- pour
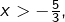
 est en-dessous de
est en-dessous de 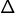
En pratique, étant donnée une fonction ![]() telle que
telle que ![]() que faire pour déterminer l’équation d’une éventuelle droite asymptote ? Voici la recette.
que faire pour déterminer l’équation d’une éventuelle droite asymptote ? Voici la recette.
On calcule d’abord :
![]()
On distingue alors trois cas :
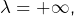 on dit que
on dit que  présente en
présente en 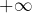 une branche parabolique d’axe
une branche parabolique d’axe 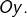 C’est par exemple le cas lorsque
C’est par exemple le cas lorsque  est un trinôme
est un trinôme 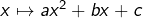 avec
avec  ou encore pour
ou encore pour 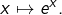
- Si
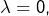 on dit que
on dit que  présente en
présente en 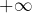 une branche parabolique d’axe
une branche parabolique d’axe 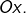 C’est notamment le cas pour
C’est notamment le cas pour 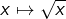 ou encore pour
ou encore pour 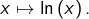
- Si
![Rendered by QuickLaTeX.com \lambda\in\left]0,+\infty\right[,](https://math-os.com/wp-content/ql-cache/quicklatex.com-c67a697cc3cdb28044af839f7652a411_l3.png) on calcule :
on calcule :
… toujours sous réserve d’existence ! Si cette limite est finie, alors la droite d’équation![Rendered by QuickLaTeX.com \[\mu={\displaystyle \lim_{x\rightarrow+\infty}\left(f\left(x\right)-\lambda x\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1acfc140ae7306e72c9ef95be30287d5_l3.png)
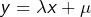 est asymptote en
est asymptote en 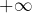 au graphe
au graphe  de
de 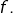
7 – Quelques études détaillées
Dans cette section, on détaille l’étude de quelques fonctions, en mettant à profit les différentes techniques présentées précédemment.
Etude n° 1
Intéressons-nous à :
![]()
Cette fonction est bien définie sur ![]() puisque
puisque ![]() pour tout
pour tout ![]() (discriminant
(discriminant ![]()
Comme la fonction racine carrée est dérivable sur ![]() on voit que
on voit que ![]() est dérivable et que :
est dérivable et que :
![]()
Il en résulte que ![]() décroît sur
décroît sur ![]() croît sur
croît sur ![]() et présente en
et présente en ![]() un minimum absolu :
un minimum absolu :
![]()
Le graphe ![]() de
de ![]() présente une symétrie d’axe
présente une symétrie d’axe ![]() puisque, pour tout
puisque, pour tout ![]() :
:
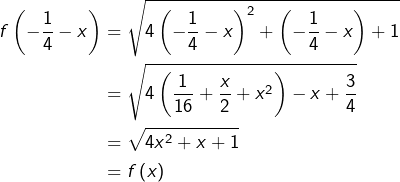
![]() est convexe, car pour tout
est convexe, car pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[ f''\left(x\right)=\frac{4}{\sqrt{4x^{2}+x+1}}-\frac{\left(8x+1\right)^{2}}{4\left(4x^{2}+x+1\right)^{3/2}} \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-159f21a73a0335c07891f4411c2773c7_l3.png)
![]()
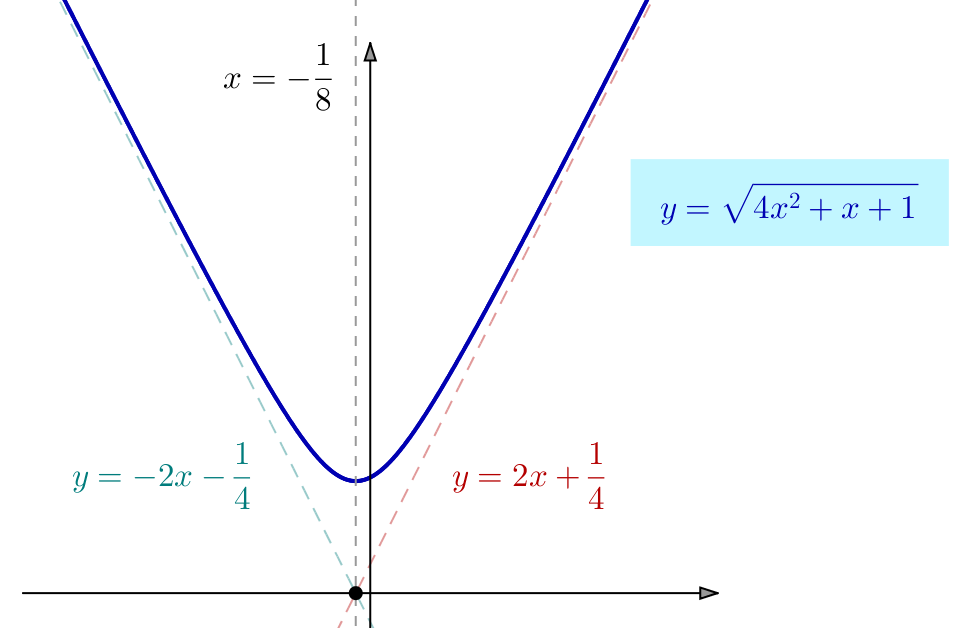
Terminons par l’étude du comportement asymptotique. Il est clair que :
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{\lim_{x\rightarrow+\infty}\frac{f\left(x\right)}{x}=2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b87cda7a73b81fd747ae8e2849f93f2a_l3.png)
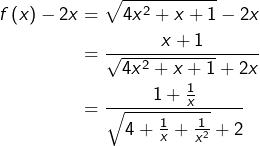
![Rendered by QuickLaTeX.com \[\boxed{\lim_{x\rightarrow+\infty}\left(f\left(x\right)-2x\right)=\frac{1}{4}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e4e6024904f67bd4e6421296cf6d367b_l3.png)
![]()
Etude n° 2
On s’intéresse à présent à :
![]()
On calcule, pour tout ![]() :
:
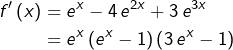
Ensuite :
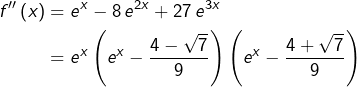
![Rendered by QuickLaTeX.com \[\alpha=\ln\left(\frac{4-\sqrt{7}}{9}\right)\simeq-1.89\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6433fea3577aa80bf7976d3b2cbc0979_l3.png)
![Rendered by QuickLaTeX.com \[\beta=\ln\left(\frac{4+\sqrt{7}}{9}\right)\simeq-0.30\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-32031a991457aa5cb614c48eb9677778_l3.png)
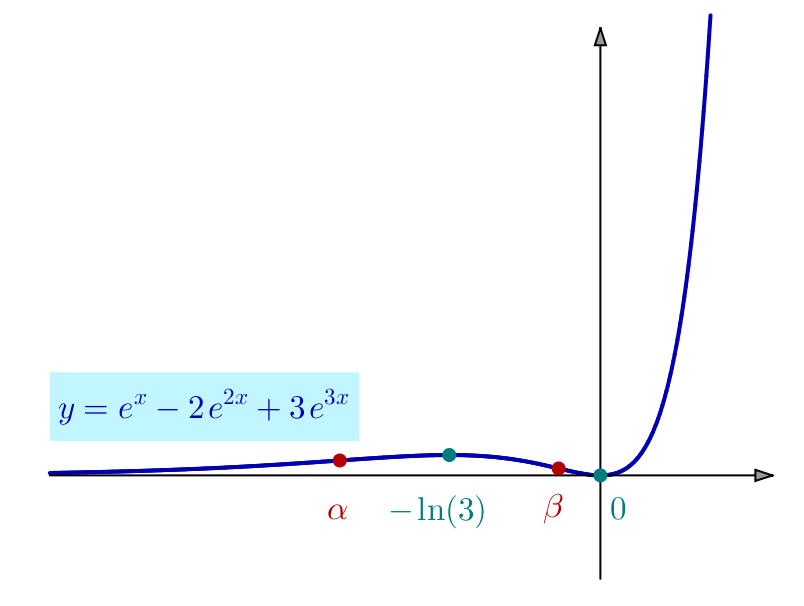
La droite d’équation ![]() est asymptote à
est asymptote à ![]() en
en ![]()
![]() présente en
présente en ![]() une branche parabolique d’axe
une branche parabolique d’axe ![]()
Etude n° 3
Considérons la fonction :
![]()
![]()
![]()
![]()
On calcule ensuite la dérivée seconde :
![]()
![]()
![]()
![]()
Par une dichotomie (non détaillée), on trouve ![]() à
à ![]() près.
près.
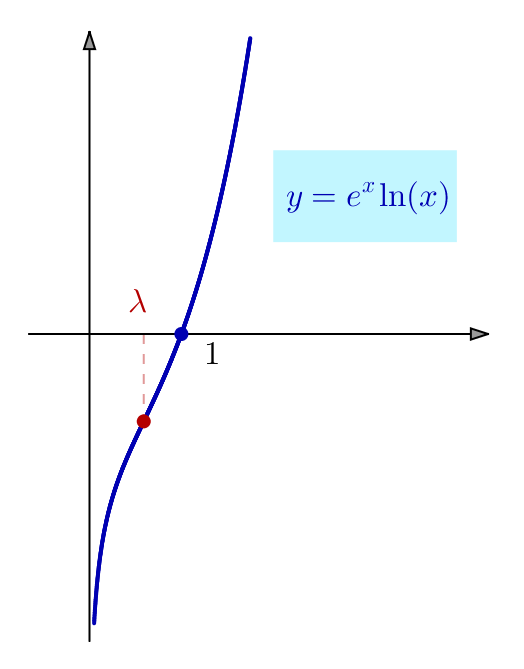
Ainsi, ![]() est concave sur
est concave sur ![]() et convexe sur
et convexe sur ![]() Le graphe présente une inflexion au point d’abscisse
Le graphe présente une inflexion au point d’abscisse ![]()
Etude n° 4
Dans cet exemple, on va voir apparaître un comportement asymptotique différent de ceux rencontrés plus haut. Posons, pour tout ![]() :
:
![]()
![]()
Cette expression est du signe de ![]() donc de
donc de ![]() car
car
![]()
La dérivée seconde de ![]() est donnée par :
est donnée par :
![]()
Pour ![]() cette expression est strictement positive.
cette expression est strictement positive.
Et pour ![]() elle est du signe contraire à :
elle est du signe contraire à : ![]()
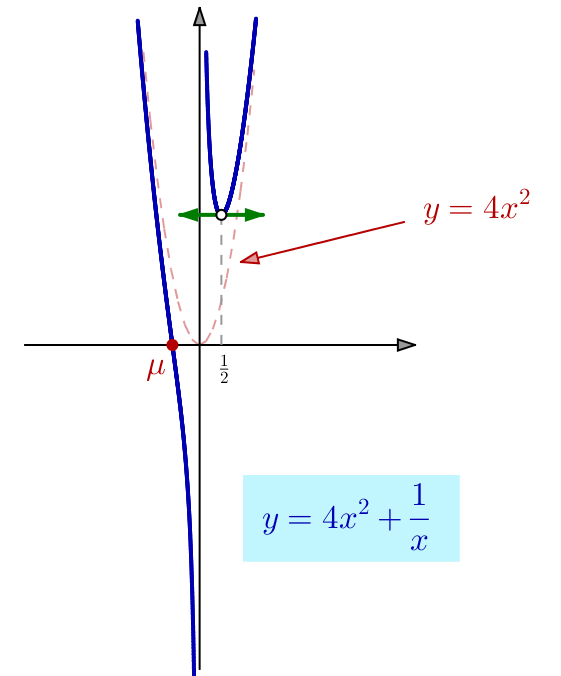
On a donc une inflexion en ![]() avec :
avec :
![]()
Lorsque ![]() on voit que
on voit que ![]() Ceci s’interprète en disant que la parabole
Ceci s’interprète en disant que la parabole ![]() d’équation
d’équation ![]() est asymptote au graphe
est asymptote au graphe ![]() de
de ![]() Ajoutons que
Ajoutons que ![]() est au-dessus de
est au-dessus de ![]() pour
pour ![]() et en-dessous pour
et en-dessous pour ![]()
Etude n° 5
On passe à l’étude des variations de :
![]()
Par définition ![]() expression bien définie pour tout
expression bien définie pour tout ![]()
La dérivée de ![]() est donnée par :
est donnée par :
![]()
![]()
![]() est définie et dérivable sur
est définie et dérivable sur ![]() et pour tout
et pour tout ![]() :
:
![]()
![]()
De même, comme :
![]()
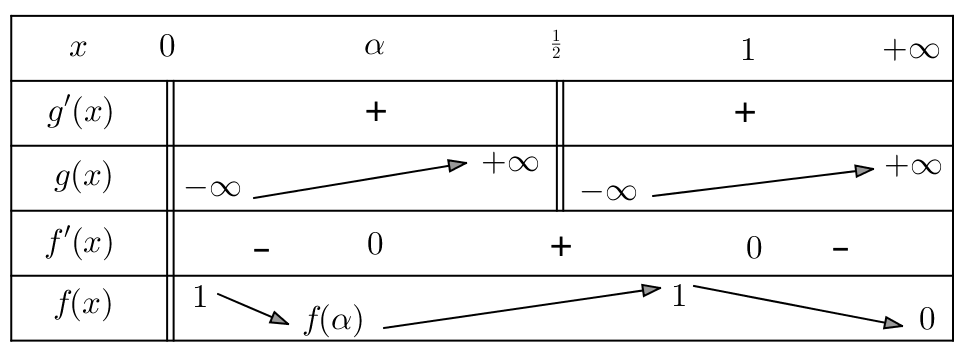
Comme ![]() possède en 0 la limite finie 1, on peut effectuer un prolongement par continuité :
possède en 0 la limite finie 1, on peut effectuer un prolongement par continuité :
![Rendered by QuickLaTeX.com \[\tilde{f}:\left[0,+\infty\right[\rightarrow\mathbb{R},\,x\mapsto\left\{ \begin{array}{cc}f\left(x\right) & \mbox{si }x>0\\\\1 & \mbox{si }x=0\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8e761ddb012d23d76056fc892832c253_l3.png)
On examine la dérivabilité de ![]() en
en ![]() Pour tout
Pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\frac{\tilde{f}\left(x\right)-\tilde{f}\left(0\right)}{x}=\frac{e^{\left(x-x^{2}\right)\ln\left(x\right)}-1}{\left(x-x^{2}\right)\ln\left(x\right)}\,\left(1-x\right)\ln\left(x\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-421d9cfb06c676ab70865ed3b33c7d5d_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\lim_{x\rightarrow0^{+}}\frac{e^{\left(x-x^{2}\right)\ln\left(x\right)}-1}{\left(x-x^{2}\right)\ln\left(x\right)}=1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-903d04f9fa033e6e434fec1b252ec41d_l3.png)
![]()
Ainsi, ![]() n’est pas dérivable en
n’est pas dérivable en ![]() Son graphe présente au point de coordonnées
Son graphe présente au point de coordonnées ![]() une demi-tangente verticale.
une demi-tangente verticale.
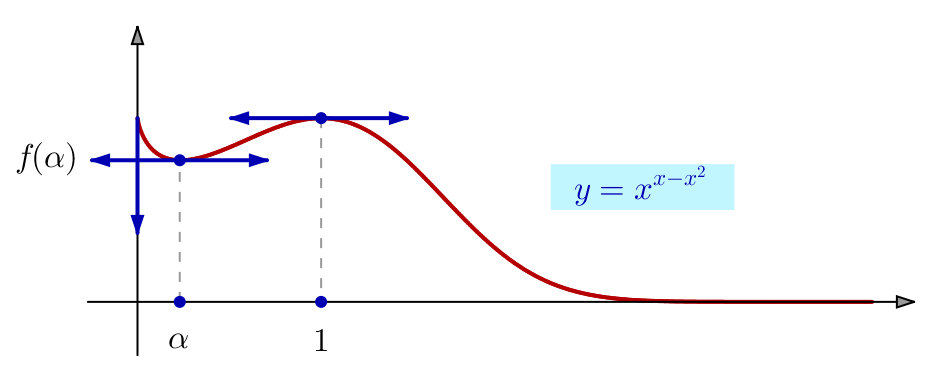
Par dichotomie, on trouve ![]() et
et ![]()
Etude n° 6
Etudions pour finir les variations de :
![]()
On calcule la dérivée :
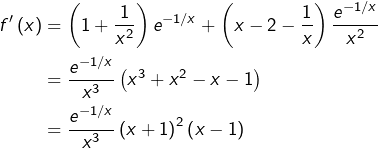
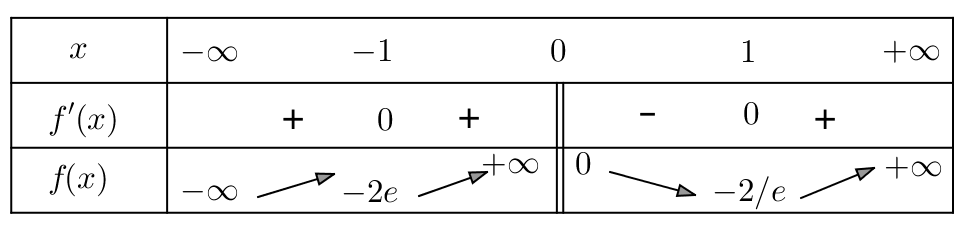
![]() n’est pas définie en
n’est pas définie en ![]() mais possède en ce point une limite à droite nulle. Si l’on note
mais possède en ce point une limite à droite nulle. Si l’on note ![]() la restriction de
la restriction de ![]() à
à ![]() on peut donc prolonger
on peut donc prolonger ![]() par continuité en posant :
par continuité en posant :
![Rendered by QuickLaTeX.com \[F\left(x\right)=\left\{ \begin{array}{cc}f\left(x\right) & \text{si }x>0\\\\0 & \text{si }x=0\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-29044edd07b67d7a7a96e1f8b7769ec1_l3.png)
On constate alors que, pour tout ![]() :
:
![]()
![]()
Ceci se traduit, pour le graphe ![]() de
de ![]() par une demi-tangente de pente nulle à l’origine.
par une demi-tangente de pente nulle à l’origine.
Pour l’étude du comportement asymptotique en ![]() on va utiliser le développement limité de l’exponentielle en 0 à l’ordre 2 :
on va utiliser le développement limité de l’exponentielle en 0 à l’ordre 2 :
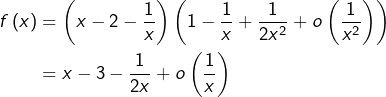
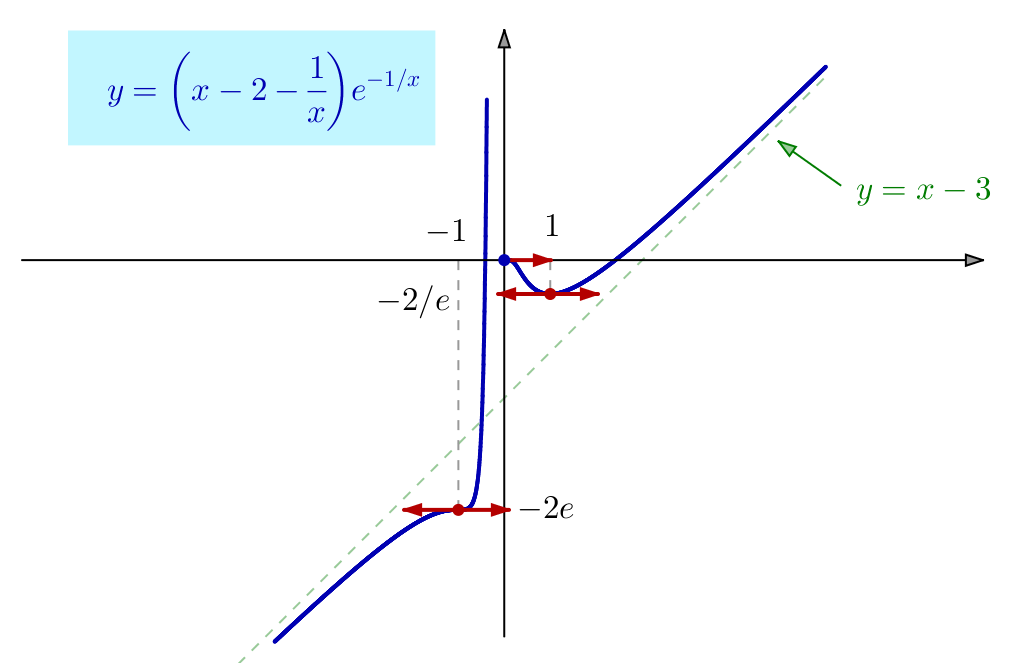
8 – Variations et Inégalités
L’étude des variations d’une fonction peut servir à établir des inégalités dont la preuve directe n’est pas accessible directement (ou à la rigueur accessible, mais pas évidente). Voici trois exemples, sous forme d’exercices corrigés :
Exercice 8
Etant donnés ![]() tels que
tels que ![]() comparer les nombres
comparer les nombres ![]() et
et ![]()
Solution proposée – Posons pour tout ![]() :
:
![]()
![]()
![]()
Exercice 9
Comparer, pour ![]() les nombres :
les nombres :
![]()
Solution proposée –
Introduisons deux fonctions ![]() et
et ![]() :
:
![]()
![]()
On constate d’une part que :
![]()
![]()
D’autre part :
![]()
![]()
Conclusion générale :
![Rendered by QuickLaTeX.com \[\boxed{\forall x\in\left[0,+\infty\right[,\thinspace x-\frac{x^{2}}{2}\leqslant\ln\left(1+x\right)\leqslant x}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5dc18374d894e00e38b900e2a81ae928_l3.png)
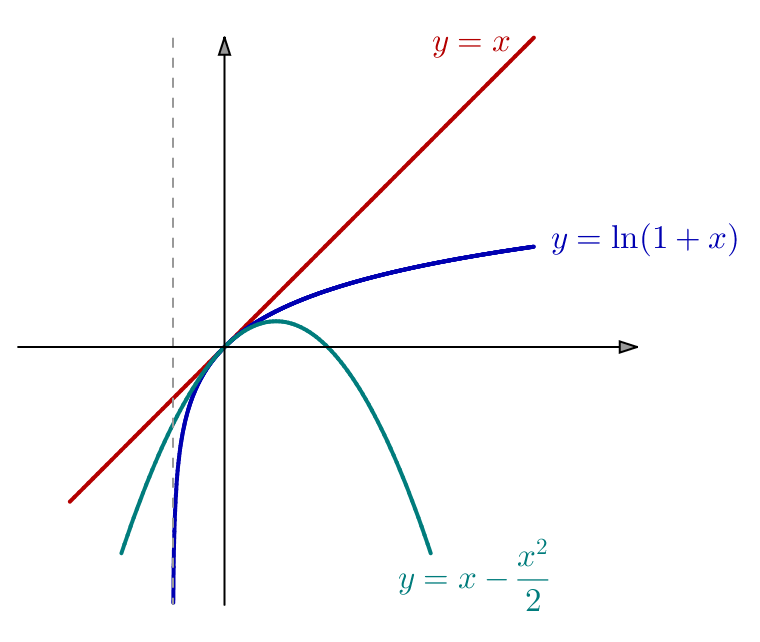
Notons que l’inégalité ![]() est vraie pour tout
est vraie pour tout ![]() ce qu’on peut voir en complétant l’étude des variations de
ce qu’on peut voir en complétant l’étude des variations de ![]() sur
sur ![]() On peut aussi éviter tout calcul :
On peut aussi éviter tout calcul : ![]() est concave (dérivée seconde négative) donc son graphe est situé en-dessous de sa tangente en
est concave (dérivée seconde négative) donc son graphe est situé en-dessous de sa tangente en ![]()
Ajoutons que pour ![]() l’autre inégalité est renversée :
l’autre inégalité est renversée :
![]()
Remarque
L’encadrement de ![]() obtenu plus haut peut encore être raffiné :
obtenu plus haut peut encore être raffiné :
![]()
![]()
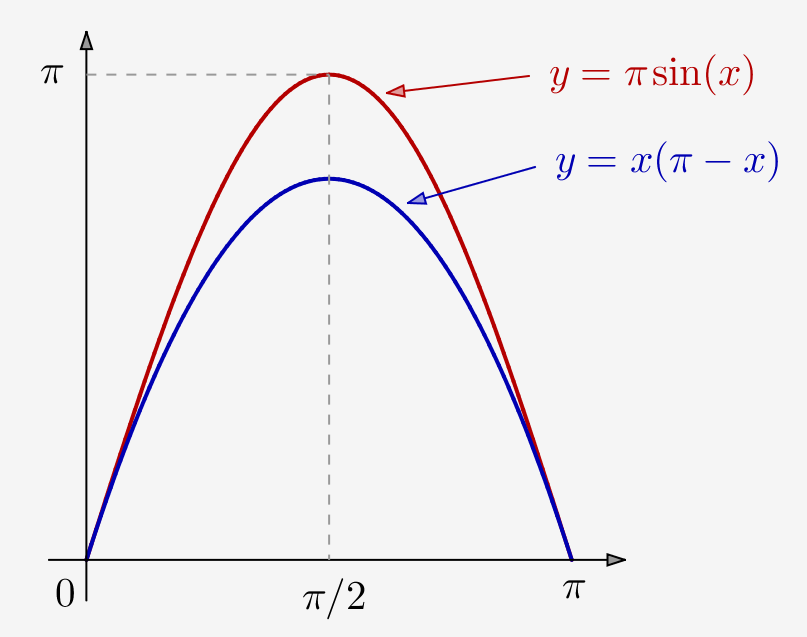
Exercice 10
Montrer que :
![]()
Solution proposée –
Posons, pour tout ![]() :
:
![]()
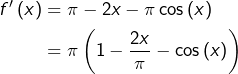
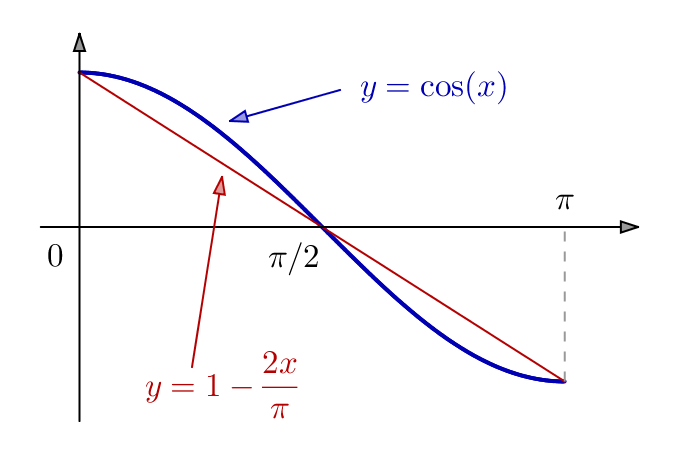
Ceci prouve que ![]() pour
pour ![]() et
et ![]() pour
pour ![]() Ainsi,
Ainsi, ![]() décroît sur
décroît sur ![]() puis croît sur
puis croît sur ![]() Et comme
Et comme ![]() on peut conclure que
on peut conclure que ![]() pour tout
pour tout ![]() comme souhaité.
comme souhaité.
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Merci monsieur pour ces preuves et observations supplémentaires 🙂
Ah oui je vois cela donnerait peut-être une alternance de convexité et concavité si l’on se servait d’un super zoom !
Bien à vous
C’est vraiment très insignifiant 🙂 , mais:
– section 2 exemple 1 et section 7 étude 1 : une seule fois l’expression n’est pas en face du = ;
– section 3 sur la périodicité, plusieurs fois la période T n’est pas affiché en format latex mais dans un encadré;
Je ne sais pas si la preuve est délicate, mais le théorème de fin de la partie 4 est élégant et je m’étonne de ne jamais l’avoir rencontré, tant l’analyse réelle d’une seule variable nous semble « familière » !
Je ne m’étais jamais fais la réflexion non plus, que si la dérivée seconde de f existe et est continue sur un intervalle, alors f alterne nécessairement les comportements concave ou convexe comme dans les exemples de fin que vous donnez. Hormis peut-être pour les cas extrêmes du type trajectoire de mouvement brownien pour la dérivée seconde, avec une infinité de zéros sur intervalle de longueur finie en dépit de la continuité (?).
Bonne journée Monsieur
Bonjour et merci, à nouveau, pour ces observations pertinentes qui permettent d’améliorer la qualité de ce travail en faisant la chasse aux coquilles 🙂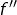 s’annule une infinité de fois et que l’ensemble des zéros de
s’annule une infinité de fois et que l’ensemble des zéros de 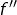 présente des points d’accumulation (penser au cas où
présente des points d’accumulation (penser au cas où 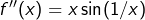 pour tout
pour tout 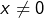 et
et 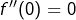 ). Il n’est pas nécessaire d’aller jusqu’au mouvement brownien 🙂
). Il n’est pas nécessaire d’aller jusqu’au mouvement brownien 🙂
Le caractérisation de la stricte monotonie d’une fonction dérivable sur un intervalle par le fait que l’ensemble des zéros de sa dérivée soit d’intérieur vide est facile à prouver. Si cet ensemble est d’intérieur non vide, cela entraîne qu’il contient un intervalle de longueur non nulle sur lequel f est constante, ce qui prouve que f n’est pas strictement monotone. Réciproquement, si f est monotone sans l’être strictement, cela prouve l’existence d’au moins un « palier », ie un intervalle de longueur non nulle sur lequel f est constante, donc de dérivée nulle.
Concernant la dérivée seconde, il faut en effet être prudent : étant donnée une fonction f, deux fois dérivable sur un intervalle I, il se peut que