Neuf énoncés d’exercices sur les calculs de sommes (fiche 02).
Prouver, le plus simplement possible, que :
![\[ \lim_{n\rightarrow\infty}\sum_{k=1}^{n}\frac{1}{\sqrt{k}}=+\infty\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6ba4f62864d7fea3de79e062770ffbcf_l3.png "Rendered by QuickLaTeX.com")
Trouver, sans chercher à raisonner par récurrence, une formule plus simple pour :
![\[ C_{n}=\sum_{k=1}^{n}\left(-1\right)^{k-1}k\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-eda3585ccf0169aac881bb23357c8abc_l3.png "Rendered by QuickLaTeX.com")
Calculer plus simplement :
![\[ \sum_{k=1}^{n}k\left(k+1\right)\left(k+2\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-35f26226dba52a7f46daabd9a319048e_l3.png "Rendered by QuickLaTeX.com")
Prouver que, pour tout entier 
:
![\[ \sum_{k=1}^{n}k!\leqslant n!+\left(n-1\right)!+\left(n-2\right)\left(n-2\right)!\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d649b664356a00a00d82fd7b1771f237_l3.png "Rendered by QuickLaTeX.com")
![\[ \lim_{n\rightarrow\infty}\frac{1}{n!}\sum_{k=1}^{n}k!\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-40c1a77c16894a2d0f69e81ffa635300_l3.png "Rendered by QuickLaTeX.com")
On note 
le 
ème nombre de Fibonacci. On rappelle que :
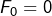et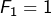 
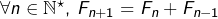
Calculer :
![\[ \sum_{n=1}^{+\infty}\,\frac{\left(-1\right)^{n+1}}{F_{n}\,F_{n+1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-94493c15a3df2777c9da26de92abaadc_l3.png "Rendered by QuickLaTeX.com")
Calculer plus simplement la somme :
![\[ S_{n}=\sum_{k=0}^{n}\frac{\binom{n}{k}}{k+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ce7861d2e96011936d1942e27c5fb90d_l3.png "Rendered by QuickLaTeX.com")
Soit 
et soient ![a_{1},\cdots,a_{n}\in\left]-1,+\infty\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-ddafc3dc3ca72f3166f87c3e12c3ca30_l3.png "Rendered by QuickLaTeX.com")
tels que 
Etablir :
![\[ \prod_{k=1}^{n}\left(1+a_{k}\right)\leqslant\sum_{k=0}^{n}\frac{S^{k}}{k!}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-548a6d8cd459b68746cb87fd7ba2dbe5_l3.png "Rendered by QuickLaTeX.com")
où l’on a posé
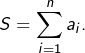
Soit 
un ensemble fini de cardinal 
Combien peut-on former de couples 
de parties de vérifiant 
?
Soit 
On lance plusieurs fois de suite une pièce de monnaie équilibrée, jusqu’à obtenir un total de 
« pile » ou de « face ». On note 
la variable aléatoire égale au nombre de lancers nécessaires. Déterminer la loi de et en déduire le calcul de :
![\[ S_{n}=\sum_{k=0}^{n}\frac{\binom{n+k}{k}}{2^{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c5ca06ed5468aaceeaf3a1b3494c8ee8_l3.png "Rendered by QuickLaTeX.com")
Cliquer ici pour accéder aux indications
Cliquer ici pour accéder aux solutions
un article sur les sommes doubles et les familles sommables serait le bienvenu merci