Solutions détaillées de neuf exercices sur les calculs de sommes (fiche 02).
Cliquer ici pour accéder aux énoncés.


La somme proposée comporte ![]() termes. Le plus petit est
termes. Le plus petit est ![]()
Par conséquent :
![Rendered by QuickLaTeX.com \[ \sum_{k=1}^{n}\frac{1}{\sqrt{k}}\geqslant n\times\frac{1}{\sqrt{n}}=\sqrt{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-24cf504760561c0ca8c6dc3804a2dd42_l3.png)
Par comparaison, on en déduit que :
![Rendered by QuickLaTeX.com \[ \boxed{\lim_{n\rightarrow\infty}\sum_{k=1}^{n}\frac{1}{\sqrt{k}}=+\infty}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3ee0ad394fc854d79ed7a58f9bf32914_l3.png)

Il est facile de calculer ![]() (pour
(pour ![]() en regroupant les termes deux par deux :
en regroupant les termes deux par deux :
![Rendered by QuickLaTeX.com \[ C_{2p}=\sum_{j=1}^{p}\left[\left(2j-1\right)-2j\right]=-p\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ca92634acd4500d2c912e20aefaf8d43_l3.png)
Il en résulte que :
![]()
Ainsi :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N}^{\star},\thinspace C_{n}=\left\{\begin{array}{cc}-\frac{n}{2} & \text{si }n\text{ est pair}\\\\\frac{n+1}{2} & \text{sinon}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7b9176181c1b60a2968cf750eb301f4e_l3.png)
Pour finir, on peut (mais ce n’est pas indispensable) regrouper ces deux formules en une seule :
![Rendered by QuickLaTeX.com \[ \boxed{\forall n\in\mathbb{N}^{\star},\thinspace C_{n}=\left(-1\right)^{n-1}\left\lfloor \frac{n+1}{2}\right\rfloor }\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9dfd9be69dee3f116d8f1fc963e53592_l3.png)

Il suffit de remarquer que, pour tout ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=1}^{n}k\left(k+1\right)\left(k+2\right)=\frac{n\left(n+1\right)\left(n+2\right)\left(n+3\right)}{4}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-45820170511e97af4e8ca5bdc0d6ac39_l3.png)
On peut montrer, plus généralement, pour tout couple ![]() d’entiers naturels non nuls :
d’entiers naturels non nuls :
![Rendered by QuickLaTeX.com \[ \sum_{k=1}^{n}\prod_{j=0}^{p}\left(k+j\right)=\frac{1}{p+2}\prod_{j=0}^{p+1}\left(n+j\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e01d3ce4d1bae380a6171bcff06195df_l3.png)
![Rendered by QuickLaTeX.com \[ \left(p+2\right)\prod_{j=0}^{p}\left(k+j\right)=\prod_{j=0}^{p+1}\left(k+j\right)-\prod_{j=-1}^{p}\left(k+j\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-feab36764d09ae2b1511d5943f2abaa3_l3.png)
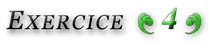
Une somme de termes peut toujours être majorée par le produit du plus grand terme par le nombre de termes (cf. exercice n° 1 de la présente fiche).
On voit ainsi que, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[ \sum_{k=1}^{n-2}k!\leqslant\left(n-2\right)\left(n-2\right)!\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-908de0c1df7d7f3c8c51f3b697141980_l3.png)
![Rendered by QuickLaTeX.com \[ \sum_{k=1}^{n}k!\leqslant n!+\left(n-1\right)!+\left(n-2\right)\left(n-2\right)!\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4939f73292c287178bcc1665d075a1ed_l3.png)
Par ailleurs, il est évident que :
![Rendered by QuickLaTeX.com \[ n!\leqslant\sum_{k=1}^{n}k!\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d9300da707fd60aa23ef68af8027ca03_l3.png)
On dispose donc, pour tout ![]() de l’encadrement :
de l’encadrement :
![Rendered by QuickLaTeX.com \[ 1\leqslant\frac{1}{n!}\sum_{k=1}^{n}k!\leqslant1+\frac{1}{n}+\frac{n-2}{n\left(n-1\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-feb7c97b305c5b843e7bc48ccf5c2eb3_l3.png)
Le théorème d’encadrement permet de conclure que :
![Rendered by QuickLaTeX.com \[ \boxed{\lim_{n\rightarrow\infty}\frac{1}{n!}\sum_{k=1}^{n}k!=1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-057f0f1cbc61c9880989131feee21642_l3.png)

Pour tout ![]() :
:
![]()
Il en résulte que le terme général de la série peut s’écrire :
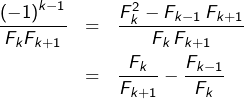
![Rendered by QuickLaTeX.com \[ \sum_{k=1}^{n}\,\frac{\left(-1\right)^{k-1}}{F_{k}\,F_{k+1}}=\sum_{k=1}^{n}\,\left(\frac{F_{k}}{F_{k+1}}-\frac{F_{k-1}}{F_{k}}\right)=\frac{F_{n}}{F_{n+1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9afab4850e68a7207106396abee9e48c_l3.png)
Or, on sait (voir par exemple ici et la remarque qui suit) que, lorsque ![]() :
:
![Rendered by QuickLaTeX.com \[ F_{n}\sim\frac{1}{\sqrt{5}}\left(\frac{1+\sqrt{5}}{2}\right)^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fc3e36d1cac5920a3aeb4fb9209d9c83_l3.png)
![Rendered by QuickLaTeX.com \[ \boxed{\sum_{k=1}^{+\infty}\,\frac{\left(-1\right)^{k-1}}{F_{k}\,F_{k+1}}=\frac{\sqrt{5}-1}{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3d418b6a693580a4bfaeb4d69f8f171f_l3.png)

Soit ![]() Posons pour tout
Posons pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[ f_{n}\left(x\right)=\sum_{k=0}^{n}\,\binom{n}{k}x^{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a46afaa357d29735a22c57097c8d94cd_l3.png)
c’est-à-dire, selon la formule du binôme (voir par exemple ici) :
![]()
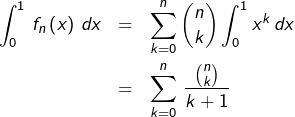
![Rendered by QuickLaTeX.com \begin{eqnarray*}\int_{0}^{1}\,f_{n}\left(x\right)\,dx & = & \int_{0}^{1}\,\left(x+1\right)^{n}\,dx\\& = & \left[\frac{\left(x+1\right)^{n+1}}{n+1}\right]{x=0}^{1}\\& = & \frac{2^{n+1}-1}{n+1}\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-f0431c4918ddc6bc8f94b4fa21c38a4f_l3.png)
Il en résulte que :
![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=0}^{n}\,\frac{\binom{n}{k}}{k+1}=\frac{2^{n+1}-1}{n+1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3823f4866529c7aecde6a253dbcdd90d_l3.png)
On peut aussi utiliser la formule du pion (si nécessaire, voir cet article) :
![]()
![Rendered by QuickLaTeX.com \[ \sum_{k=0}^{n}\,\frac{\binom{n}{k}}{k+1}=\frac{1}{n+1}\sum_{k=0}^{n}\binom{n+1}{k+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ad90ec1875f2c2f6d54f80c13c7f6fb1_l3.png)
En ré-indexant cette dernière somme, il vient :
![Rendered by QuickLaTeX.com \[ \sum_{k=0}^{n}\,\frac{\binom{n}{k}}{k+1}=\frac{1}{n+1}\sum_{j=1}^{n+1}\binom{n+1}{j}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b81084c4efe6beceffb8877ac214a676_l3.png)
Or, on sait par la formule du binôme que :
![Rendered by QuickLaTeX.com \[ \sum_{j=1}^{n+1}\binom{n+1}{j}=\left(1+1\right)^{n+1}-1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-80d1c24cbb8d97c256156e90ba76167c_l3.png)

D’après l’inégalité entre moyennes géométrique et arithmétique pour ![]() réels positifs :
réels positifs :
![Rendered by QuickLaTeX.com \[ \left[\prod_{k=1}^{n}\left(1+a_{k}\right)\right]^{1/n}\leqslant\frac{1}{n}\sum_{k=1}^{n}\left(1+a_{k}\right)=1+\frac{S}{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bdcf8dc12ba3f187114a17ffd371965e_l3.png)
Donc, par croissance de ![]() sur
sur ![]() :
:
![Rendered by QuickLaTeX.com \[ \prod_{k=1}^{n}\left(1+a_{k}\right)\leqslant\left(1+\frac{S}{n}\right)^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bb8a42e98490ae548ce1b926fec411ac_l3.png)
![Rendered by QuickLaTeX.com \[ \prod_{k=1}^{n}\left(1+a_{k}\right)\leqslant\sum_{k=0}^{n}\binom{n}{k}\left(\frac{S}{n}\right)^{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-64c347b0e98060b2d0359de819d01101_l3.png)
Or, pour tout
![Rendered by QuickLaTeX.com \[ \frac{\binom{n}{k}}{n^{k}}=\frac{1}{k!}\prod_{i=1}^{k}\frac{n-i+1}{n}\leqslant\frac{1}{k!}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c6d6ec7e466de6b26bd40a75f07baff7_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\prod_{k=1}^{n}\left(1+a_{k}\right)\leqslant\sum_{k=0}^{n}\frac{S^{k}}{k!}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c43cb4e446b2a7b5f1823f54be96311c_l3.png)

Pour ![]() fixé, notons
fixé, notons ![]() l’ensemble des parties
l’ensemble des parties ![]() de
de ![]() vérifiant
vérifiant ![]() On cherche à calculer
On cherche à calculer ![]() avec :
avec :
![]()
![]()
Par ailleurs, le cardinal du produit cartésien de deux ensembles finis est égal au produit des cardinaux, donc :
![]()
On classe à présent les parties de ![]() selon leur cardinal, ce qui revient à former des « paquets » de termes dans la somme ci-dessus. Chaque paquet renferme les termes associés aux parties
selon leur cardinal, ce qui revient à former des « paquets » de termes dans la somme ci-dessus. Chaque paquet renferme les termes associés aux parties ![]() de même cardinal
de même cardinal ![]() :
:
![Rendered by QuickLaTeX.com \[ \text{card}\left(X\right)=\sum_{k=0}^{n}\sum_{{A\subset E\atop \text{card}\left(A\right)=k}}\text{card}\left(X_{A}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9ce43911a47bab3e40288892ead84865_l3.png)
Pour finir, il faut voir deux choses :
- Pour
 donné, il existe
donné, il existe 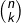 parties de
parties de  ayant pour cardinal
ayant pour cardinal 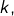
- Si
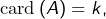 alors
alors 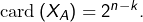 En effet, les parties
En effet, les parties 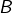 de
de  vérifiant
vérifiant 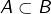 sont exactement les
sont exactement les  avec
avec 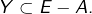 Or
Or 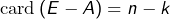 et il existe donc
et il existe donc 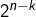 telles parties
telles parties 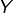 donc
donc 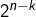 telles parties
telles parties 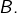
Bref :
![Rendered by QuickLaTeX.com \[ \text{card}\left(X\right)=\sum_{k=0}^{n}\binom{n}{k}2^{n-k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-07a3a21e3c10c444cd64c1878cc3c6db_l3.png)
![]()

Il paraît difficile d’obtenir ![]() « pile » ou
« pile » ou ![]() « face » en
« face » en ![]() lancers ou moins !
lancers ou moins !
Par ailleurs, si les ![]() premiers lancers ont donné autant de « pile » que de « face », on est sûr de totaliser
premiers lancers ont donné autant de « pile » que de « face », on est sûr de totaliser ![]() « pile » ou
« pile » ou ![]() « face » au coup suivant.
« face » au coup suivant.
Les valeurs prises par la variable aléatoire ![]() sont donc comprises entre
sont donc comprises entre ![]() et
et ![]()
Réciproquement, si ![]() alors
alors ![]() peut prendre la valeur
peut prendre la valeur ![]() c’est par exemple le cas si les
c’est par exemple le cas si les ![]() premiers lancers produisent la séquence :
premiers lancers produisent la séquence :
![]()
Bref :
![]()
Considérons maintenant l’événement ![]() pour un certain
pour un certain ![]() Pour qu’il se réalise, il faut et il suffit que l’un des deux scénarios suivants se produise :
Pour qu’il se réalise, il faut et il suffit que l’un des deux scénarios suivants se produise :
- scénario 1 : les
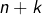 premiers lancers donnent
premiers lancers donnent  « pile » et
« pile » et 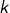 « face » et le
« face » et le 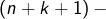 ème lancer donne « pile »
ème lancer donne « pile » - scénario 2 : les
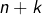 premiers lancers donnent
premiers lancers donnent 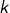 « pile » et
« pile » et  « face » et le
« face » et le 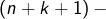 ème lancer donne « face »
ème lancer donne « face »
Or, l’ensemble des ![]() premiers lancers peut conduire à
premiers lancers peut conduire à ![]() séquences équiprobables, parmi lesquelles
séquences équiprobables, parmi lesquelles ![]() réalisent le scénario 1 et autant réalisent le scénario 2.
réalisent le scénario 1 et autant réalisent le scénario 2.
Par conséquent :
![]()
Il s’ensuit que :
![Rendered by QuickLaTeX.com \[ \sum_{k=0}^{n}\frac{\binom{n+k}{k}}{2^{n+k}}=1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c55d16a1f9ad07e87c7a5a53a8e3218b_l3.png)
![Rendered by QuickLaTeX.com \[ \boxed{\frac{\binom{n+k}{k}}{2^{k}}=2^{n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-02464c9475b7c2cb9e07611f8ee9b8ba_l3.png)
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
