Exercices de calcul de sommes - 01

Exercices de calcul de sommes – 01

Neuf énoncés d’exercices sur les calculs de sommes (fiche 01).

On considère quatre entiers naturels $A,B,r,n$ tels que :

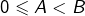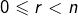et l’on note $E$ l’ensemble des entiers $k$ vérifiant :

$An+r\leqslant k<Bn+r\qquad\text{et}\qquad k\equiv r\pmod n$

Calculer la somme des éléments de $E$ .

Calculer explicitement, pour tout $n\in\mathbb{N}^{\star}$ , les sommes :

$A_{n}=\sum_{k=1}^{n}\binom{n}{k}2^{1-k}$

On note $F_{n}$ le $n-$ ème nombre de Fibonacci. On rappelle que :

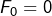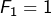
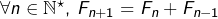
Calculer 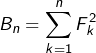$\displaystyle{B_{n}=\sum_{k=1}^{n}F_{k}^{2}}$ et interpréter géométriquement la formule obtenue.

On pose pour tout entier $n\geqslant2$ :

$B_{n}=\sum_{k=1}^{n-1}\frac{1}{\sqrt{k\left(n-k\right)}}$

Trouver un réel $\lambda>0$ tel que $\forall n\geqslant2,\,B_{n}\geqslant\lambda$ .

Soit $n\geqslant1$ et soient $a_{1},\cdots,a_{n}>0.$ On pose :

$m=\min_{1\leqslant i\leqslant n}a_{i}\qquad\text{et}\qquad M=\max_{1\leqslant i\leqslant n}a_{i}$

Prouver que :

$2n\sqrt{\frac{m}{M}}\leqslant\sum_{i=1}^{n}\frac{a_{i}}{M}+\sum_{i=1}^{n}\frac{m}{a_{i}}\leqslant n\left(1+\frac{m}{M}\right)$

Soit $q\in\mathbb{N}^{\star}.$ Montrer qu’il existe $M>0$ tel que, pour tout $n\in\mathbb{N}^{\star}$ :

$\left|\sum_{k=0}^{n}\cos\left(\frac{k\pi}{q}\right)\right|\leqslant M$

Soient $n\in\mathbb{N}^{\star}$ et $z\in\mathbb{C}.$ On pose $\omega=e^{2i\pi/n}.$ Calculer plus simplement :

$S_{n}\left(z\right)=\sum_{k=0}^{n-1}\,\left(z+\omega^{k}\right)^{n}$

Etablir, pour tout $n\in\mathbb{N}^{\star}$ :

$\sum_{k=1}^{n}\,\frac{\left(-1\right)^{k-1}}{k}\,\binom{n}{k}=\sum_{k=1}^{n}\,\frac{1}{k}$

Soit $n\geqslant1$ et soient $a_{1},\cdots,a_{n}>0.$ On pose, pour tout $q\in\llbracket1,n-1\rrbracket$ :

$S_{q}=\sum_{i=1}^{q}a_{i}-\sum_{i=q+1}^{n}a_{i}$

et l’on convient que :

$S_{n}=-S_{0}=\sum_{i=1}^{n}a_{i}$

Prouver qu’il existe $j\in\llbracket0,n-1\rrbracket$ tel que : $\displaystyle{\left|S_{j}\right|\leqslant\max_{1\leqslant i\leqslant n}a_{i}}$

Cliquer ici pour accéder aux indications
Cliquer ici pour accéder aux solutions

Partager cet article

errard 9 Juil 2019 Répondre

surtout les doubles sommes et les familles sommables

merci a l avance
errard 8 Juil 2019 Répondre

je n arrive pas a accéder aux solutions pour les sommes
1. René Adad 8 Juil 2019 Répondre
  
  Un peu de patience
  ça arrive !
  1. René Adad 8 Juil 2019 Répondre
    
    Les indications sont en place.
    
    Les solutions arriveront au plus tard en soirée
    
    En attendant, bonne réflexion ! Et si vous souhaitez me soumettre d’autres exercices récalcitrants sur ce thème, n’hésitez pas et je verrai ce que je peux faire.