Solutions détaillées de neuf exercices sur les calculs de sommes (fiche 01).
Cliquer ici pour accéder aux énoncés.


La somme à calculer est :
![Rendered by QuickLaTeX.com \[ \sigma=\sum_{k=A}^{B-1}\left(kn+r\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7cfae1be4c8a793a7438cb9b3a34f94b_l3.png)
- de raison
 ,
, - de premier terme
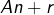 ,
, - de dernier terme
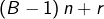 ,
, - qui comporte
 termes
termes
Par conséquent :
![]()
![]()

Pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[ A_{n}=2\left[\left(\sum_{k=0}^{n}\binom{n}{k}2^{-k}\right)-1\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d38dd906c49aea21a563e127302a331a_l3.png)
![Rendered by QuickLaTeX.com \[ \sum_{k=0}^{n}\binom{n}{k}2^{-k}=\left(1+\frac12\right)^n=\left(\frac{3}{2}\right)^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a835d46c3b168c82a7f94235e33f2215_l3.png)
![Rendered by QuickLaTeX.com \[ \boxed{A_{n}=2\left[\left(\frac{3}{2}\right)^{n}-1\right]}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-96289636d00bcbbae47867318fa50c76_l3.png)

En remarquant que, pour tout entier ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[ B_{n}=\sum_{k=1}^{n}F_{k}\left(F_{k+1}-F_{k-1}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7ca6e7057e87f9533c0f628c5b6bf187_l3.png)
![Rendered by QuickLaTeX.com \[ B_{n}=\sum_{k=1}^{n}\left(F_{k}F_{k+1}-F_{k-1}F_{k}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-148c53195fd6a600273ebdab3531d0da_l3.png)
![]()
![Rendered by QuickLaTeX.com \[ \boxed{\sum_{k=1}^{n}F_{k}^{2}=F_{n}F_{n+1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d39d0b442405924767191e5de62810f5_l3.png)
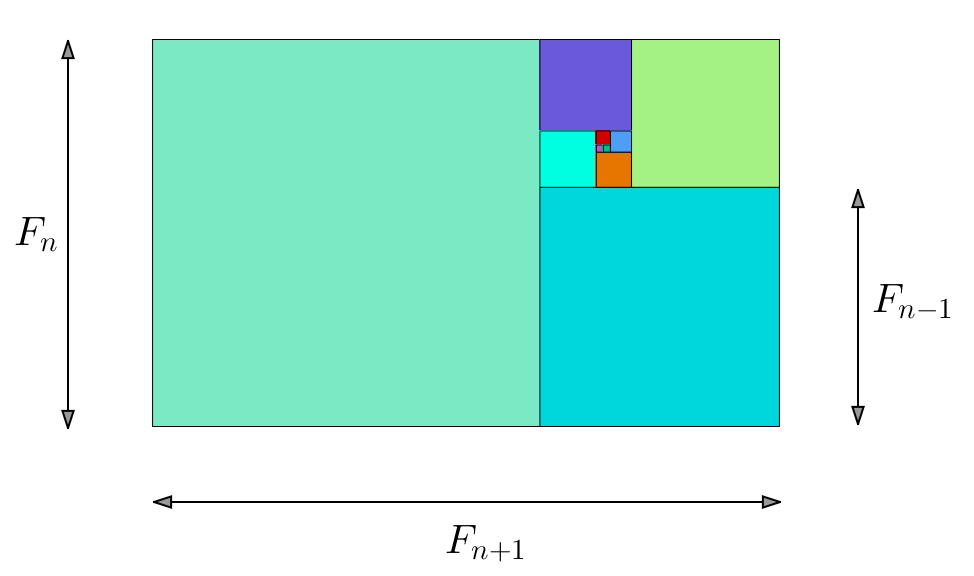

On voit, en écrivant :
![]()
Donc, pour tout
![Rendered by QuickLaTeX.com \[ \sqrt{k\left(n-k\right)}=n\sqrt{\frac{k}{n}\left(1-\frac{k}{n}\right)}\leqslant\frac{n}{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-905cbf892aebd1d42d5c10e81670b80d_l3.png)
![Rendered by QuickLaTeX.com \[ \sum_{k=1}^{n-1}\frac{1}{\sqrt{k\left(n-k\right)}}\geqslant\frac{n-1}{2n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a74e47e34ab0ca97b1a8830dd4f6c8ba_l3.png)
![Rendered by QuickLaTeX.com \[ \boxed{\sum_{k=1}^{n-1}\frac{1}{\sqrt{k\left(n-k\right)}}\geqslant\frac{1}{4}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6726a75c9beb7eb556e1411ab23034e5_l3.png)
Remarque
Ce n’était pas demandé, mais on peut montrer que :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}\sum_{k=1}^{n-1}\frac{1}{\sqrt{k\left(n-k\right)}}=\pi\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3613b7004a5c72d42cf9ae11315f9590_l3.png)

Considérons la fonction :
![]()
![]()
On voit ainsi que ![]() décroît sur
décroît sur ![]() et croît sur
et croît sur ![]() puis que :
puis que :
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[ \boxed{2n\sqrt{\frac{m}{M}}\leqslant\sum_{i=1}^{n}\frac{a_{i}}{M}+\sum_{i=1}^{n}\frac{m}{a_{i}}\leqslant n\left(1+\frac{m}{M}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-45dd6afd1dcffae889f52984f6ea3d36_l3.png)

Posons ![]() de sorte que pour tout
de sorte que pour tout ![]() et d’après la formule de Moivre :
et d’après la formule de Moivre :
![]()
![Rendered by QuickLaTeX.com \[ \sum_{k=0}^{n}\cos\left(\frac{k\pi}{q}\right)=\text{Re}\left(\sum_{k=0}^{n}z^{k}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d3f366e9e2eab086b89f2c844f8000c5_l3.png)
![Rendered by QuickLaTeX.com \[ \sum_{k=0}^{n}\cos\left(\frac{k\pi}{q}\right)=\text{Re}\left(\frac{1-z^{n+1}}{1-z}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-442c55ddb5fa362ac6f4495b4681f088_l3.png)
![Rendered by QuickLaTeX.com \[ \left|\sum_{k=0}^{n}\cos\left(\frac{k\pi}{q}\right)\right|\leqslant\left|\frac{1-z^{n+1}}{1-z}\right|\leqslant\frac{2}{\left|1-z\right|}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5d8893eb6023f9bbc523a0071a0cef37_l3.png)
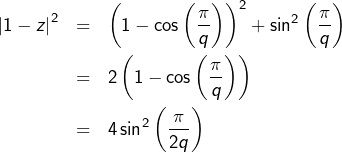
![Rendered by QuickLaTeX.com \[ \boxed{{\displaystyle M=}\frac{1}{\sin\left(\frac{\pi}{2q}\right)}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bab767772b68b5bde7ff0da3cb4753de_l3.png)

On développe, pour tout ![]() l’expression
l’expression ![]() par la formule du binôme :
par la formule du binôme :
![Rendered by QuickLaTeX.com \[ \left(z+\omega^{k}\right)^{n}=\sum_{j=0}^{n}\binom{n}{j}z^{n-j}\omega^{kj}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ca403a49866439da38e44af5f8b00fe9_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*}S_{n}\left(z\right) & = & \sum_{k=0}^{n-1}\left(z+\omega^{k}\right)^{n}\\ & = & \sum_{k=0}^{n-1}\left(\sum_{j=0}^{n}\,\binom{n}{j}z^{n-j}\omega^{kj}\right)\\& = & \sum_{j=0}^{n}\left[\binom{n}{j}z^{n-j}\left(\sum_{k=0}^{n-1}\,\omega^{kj}\right)\right]\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-627d1514f30650ce7a0e5b328db46514_l3.png)
L’expression
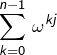 est une somme géométrique de raison
est une somme géométrique de raison ![Rendered by QuickLaTeX.com \[ \sum_{k=0}^{n-1}\,\omega^{kj}=\left\{\begin{array}{cc}n & \textrm{ si }j\in\left\{0,n\right\} \\\\\frac{1-\omega^{nj}}{1-\omega^{j}}=0 & \text{sinon} \end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-50b4a4d4c9c31b4e2737bd84404fcc4f_l3.png)
![]()

Posons :
![Rendered by QuickLaTeX.com \[ f_{n}\left(t\right)=\sum_{k=1}^{n}\,\frac{\left(-1\right)^{k-1}}{k}\binom{n}{k}t^{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b12137466a4ed0d1cdf54ae51ec7ce64_l3.png)
![Rendered by QuickLaTeX.com \[ f_{n}'\left(t\right)=\sum_{k=1}^{n}\,\left(-1\right)^{k-1}\binom{n}{k}t^{k-1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9ef3180069f2423154423a7ffdd34e08_l3.png)
![Rendered by QuickLaTeX.com \[ f_{n}'\left(t\right)=-\frac{1}{t}\,\sum_{k=1}^{n}\,\left(-1\right)^{k}\binom{n}{k}t^{k}=\frac{1-\left(1-t\right)^{n}}{t}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c44be435d5028cf9e3ef74b23ab4f673_l3.png)
![Rendered by QuickLaTeX.com \[ f_{n}'\left(t\right)=\sum_{k=0}^{n-1}\,\left(1-t\right)^{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c2fccad7f230f1989e6e6c8b1677d327_l3.png)
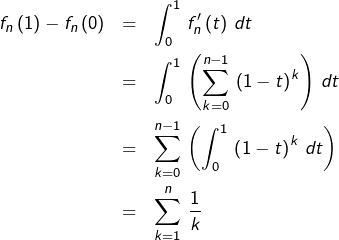
Vu que
![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=1}^{n}\,\frac{\left(-1\right)^{k-1}}{k}\binom{n}{k}=\sum_{k=1}^{n}\,\frac{1}{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1f07782d9ebf61646eda7095005c2f64_l3.png)

Comme ![]() et
et ![]() alors il existe
alors il existe ![]() tel que
tel que ![]()
Mais ![]() donc
donc ![]() et
et ![]() . On constate alors, en posant
. On constate alors, en posant ![]() que :
que :
![]()
![]()
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
