
Dans cet article, je vous propose d’examiner une notion qui se situe au carrefour de la géométrie euclidienne, de l’algèbre linéaire et de la topologie des espaces normés.
Le point de départ choisi est un résultat important du cours d’algèbre :
Théorème (du supplémentaire orthogonal)
Soit ![]() est un espace vectoriel réel, muni d’un produit scalaire.
est un espace vectoriel réel, muni d’un produit scalaire.
Pour tout sous-espace ![]() de dimension finie :
de dimension finie :
![]()
Après quelques rappels préalables, nous donnerons une preuve de ce résultat, puis nous tâcherons d’en explorer un peu les contours.
1 – Produit scalaire et orthogonalité : rapide survol
Dans tout ce qui suit, ![]() désigne un
désigne un ![]() espace vectoriel muni d’un produit scalaire : c’est ce qu’on appelle parfois un espace préhilbertien réel. Si de plus
espace vectoriel muni d’un produit scalaire : c’est ce qu’on appelle parfois un espace préhilbertien réel. Si de plus ![]() est de dimension finie, on parle plutôt d’espace vectoriel euclidien.
est de dimension finie, on parle plutôt d’espace vectoriel euclidien.
Si ![]() sont deux vecteurs de
sont deux vecteurs de ![]() leur produit scalaire est noté
leur produit scalaire est noté ![]() Rappelons qu’un produit scalaire est une » forme bilinéaire symétrique définie positive « , ce qui signifie que :
Rappelons qu’un produit scalaire est une » forme bilinéaire symétrique définie positive « , ce qui signifie que :
- [ linéarité à gauche ] pour tous
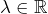 et
et 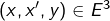 :
:![Rendered by QuickLaTeX.com \[\left(\lambda x+x'\mid y\right)=\lambda\left(x\mid y\right)+\left(x'\mid y\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bcbec80830cfc7fbac684e5b1641679b_l3.png)
- [ symétrie ] pour tout
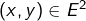 :
:![Rendered by QuickLaTeX.com \[\left(x\mid y\right)=\left(y\mid x\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d8c343bc86fc9d59d743f0bdbd6d3ddb_l3.png)
- [ définie positivité ] pour tout
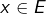 :
:
avec égalité seulement si![Rendered by QuickLaTeX.com \[\left(x\mid x\right)\geqslant0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-220e09994c9a8c47b78d99f990502d42_l3.png)
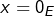
➡ Linéarité à gauche et symétrie se combinent pour donner la linéarité à droite, d’où la bilinéarité.
L’application :
![]()
Lorsque ![]() les vecteurs
les vecteurs ![]() et
et ![]() sont dits orthogonaux. Une famille orthogonale est, par définition, composée de vecteurs deux à deux orthogonaux.
sont dits orthogonaux. Une famille orthogonale est, par définition, composée de vecteurs deux à deux orthogonaux.
Quelques résultats fondamentaux :
- Toute famille orthogonale composée de vecteurs non nuls est libre.
- Toute famille orthogonale
 vérifie la formule de Pythagore :
vérifie la formule de Pythagore :![Rendered by QuickLaTeX.com \[\Vert x_{1}+\cdots+x_{r}\Vert^{2}=\left\Vert x_{1}\right\Vert ^{2}+\cdots+\left\Vert x_{r}\right\Vert ^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5464d855a5a4e2229d5a579eee08ec72_l3.png)
- Si
 est de dimension finie, alors
est de dimension finie, alors  possède des bases orthonormales, c’est-à-dire des bases composées de vecteurs unitaires (ie : de norme 1) et deux à deux orthogonaux. En outre, si
possède des bases orthonormales, c’est-à-dire des bases composées de vecteurs unitaires (ie : de norme 1) et deux à deux orthogonaux. En outre, si  est une telle base alors pour tout
est une telle base alors pour tout 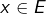 :
:
d’où (d’après la formule de Pythagore) :![Rendered by QuickLaTeX.com \[x=\sum_{i=1}^{n}\left(x\mid e_{i}\right)e_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2da70d7911f7a94ce14f7a564e1daeee_l3.png)
![Rendered by QuickLaTeX.com \[\left\Vert x\right\Vert ^{2}=\sum_{i=1}^{n}\left(x\mid e_{i}\right)^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-dc424823b088bc38f8ab4c00b38381f0_l3.png)
Si ![]() est une partie quelconque de
est une partie quelconque de ![]() l’orthogonal de
l’orthogonal de ![]() désigne l’ensemble des vecteurs de
désigne l’ensemble des vecteurs de ![]() qui sont orthogonaux à tout vecteur de
qui sont orthogonaux à tout vecteur de ![]() Il s’agit d’un sous-espace vectoriel de
Il s’agit d’un sous-espace vectoriel de ![]() qu’on note
qu’on note ![]()
On vérifie que :
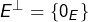
- si
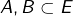 vérifient
vérifient 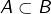 alors
alors 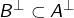
- pour tout
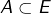 :
: 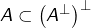
Remarque
Le premier de ces trois points se justifie par le fait que si un vecteur est orthogonal à tout vecteur de ![]() , alors il est en particulier orthogonal à lui-même, donc nul.
, alors il est en particulier orthogonal à lui-même, donc nul.
Cette petite chose est très couramment utilisée pour prouver une égalité entre vecteurs d’espace préhilbertien. L’exercice qui suit en donne une illustration.
Exercice
On considère un espace euclidien ![]() ainsi qu’une famille
ainsi qu’une famille ![]() de vecteurs de
de vecteurs de ![]()
Montrer que si ![]() est génératrice de
est génératrice de ![]() alors l’endomorphisme
alors l’endomorphisme
![Rendered by QuickLaTeX.com \[f:E\rightarrow E,\thinspace x\mapsto\sum_{i=1}^{q}\left(x\mid v_{i}\right)v_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f4c4c780e1483df9f55c326b5eb7ffe9_l3.png)
Solution proposée (cliquer pour déplier / replier)
Observons que si ![]() alors :
alors :
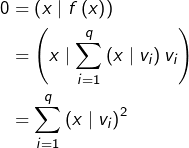
2 – Le théorème du supplémentaire orthogonal
On prouve ici le théorème énoncé dans le préambule de l’article.
Si vous préférez suivre la démonstration détaillée en vidéo, je vous renvoie au troisième épisode d’une séquence consacrée à l’étude des projecteurs :

Les hypothèses indiquent que ![]() est de dimension finie (condition réalisée, en particulier, si
est de dimension finie (condition réalisée, en particulier, si ![]() est lui-même de dimension finie). On peut donc considérer une base de
est lui-même de dimension finie). On peut donc considérer une base de ![]() et, tant qu’à faire, une base orthonormale
et, tant qu’à faire, une base orthonormale ![]() de
de ![]() Bien entendu,
Bien entendu, ![]() désigne la dimension de
désigne la dimension de ![]()
On veut prouver que ![]() c’est-à-dire que tout vecteur de
c’est-à-dire que tout vecteur de ![]() peut s’écrire, de manière unique, comme la somme d’un vecteur de
peut s’écrire, de manière unique, comme la somme d’un vecteur de ![]() et d’un vecteur de
et d’un vecteur de ![]()
On raisonne par Analyse / Synthèse.
Partie « Analyse »
Soit ![]() Supposons que
Supposons que ![]() avec
avec ![]() et
et ![]()
On peut exprimer ![]() dans la base
dans la base ![]() :
:
![Rendered by QuickLaTeX.com \[a=\sum_{i=1}^{r}\lambda_{i}e_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f549244953f89d6300ee01c09ec818c7_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\left(x\mid e_{j}\right) & = \left(a\mid e_{j}\right)+\left(b\mid e_{j}\right)\\& = \left[\sum_{i=1}^{r}\lambda_{i}\left(e_{i}\mid e_{j}\right)\right]+\left(b\mid e_{j}\right)\end{split}\end{equation*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-b7fafb222f887a22a0ae8e857850586e_l3.png)
Mais la famille ![]() est orthonormale et
est orthonormale et ![]() donc :
donc :
![]()
On a montré que si un couple ![]() convient, alors il s’agit nécessairement de :
convient, alors il s’agit nécessairement de :
![Rendered by QuickLaTeX.com \[\left\{\begin{array}{ccc}a & = & {\displaystyle \sum_{i=1}^{r}\left(x\mid e_{i}\right)e_{i}}\\\\b & = & x-{\displaystyle \sum_{i=1}^{r}\left(x\mid e_{i}\right)e_{i}}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-042c8a674f744eb115940cdf8cbcde85_l3.png)
Partie « Synthèse »
Réciproquement, si l’on définit ![]() et
et ![]() par ces formules, alors d’évidence
par ces formules, alors d’évidence ![]() et
et ![]() Il reste juste à vérifier que
Il reste juste à vérifier que ![]()
Vu que la famille ![]() engendre
engendre ![]() il suffit de prouver que
il suffit de prouver que ![]() pour tout
pour tout ![]()
Or, c’est bien le cas :
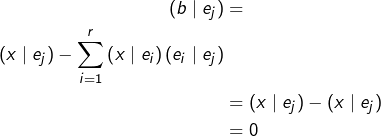
Ceci termine la preuve.
3 – Projecteurs orthogonaux
D’une manière générale, lorsqu’un espace vectoriel ![]() se décompose en la somme directe de deux sous-espaces supplémentaires, disons
se décompose en la somme directe de deux sous-espaces supplémentaires, disons ![]() on dispose du projecteur sur
on dispose du projecteur sur ![]() parallèlement à
parallèlement à ![]() qu’on peut noter
qu’on peut noter ![]()
Pour tout ![]() on sait qu’il existe un unique couple
on sait qu’il existe un unique couple ![]() tel que
tel que ![]() Par définition
Par définition ![]() est l’application de
est l’application de ![]() dans lui-même qui à
dans lui-même qui à ![]() associe
associe ![]()
On vérifie aisément que :
 est linéaire (c’est un endomorphisme de
est linéaire (c’est un endomorphisme de 
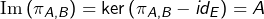
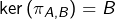
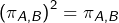
Tous ces résultats sont entièrement détaillés dans la vidéo ci-dessous, à laquelle on pourra se reporter si nécessaire :

Dans le cas particulier d’un espace préhilbertien réel ![]() et d’un sous-espace
et d’un sous-espace ![]() de dimension finie, on a vu plus haut que
de dimension finie, on a vu plus haut que ![]() On peut donc considérer le projecteur sur
On peut donc considérer le projecteur sur ![]() parallèlement à
parallèlement à ![]() , c’est-à-dire l’endomorphisme
, c’est-à-dire l’endomorphisme ![]()
C’est ce qu’on appelle le projecteur orthogonal sur ![]() qu’on note plutôt
qu’on note plutôt ![]()
Si ![]() est une base orthonormale de
est une base orthonormale de ![]() alors :
alors :
![Rendered by QuickLaTeX.com \[ \forall x\in E,\thinspace p_{F}\left(x\right)=\sum_{i=1}^{r}\left(x\mid e_{i}\right)e_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e8b6458c5ac9f196c54414bd1f322557_l3.png)
On en déduit, d’après la formule de Pythagore :
![Rendered by QuickLaTeX.com \[\left\Vert p_{F}\left(x\right)\right\Vert ^{2}=\sum_{i=1}^{r}\left(x\mid e_{i}\right)^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-22bec7850ce1e96f0410aab039bd1f70_l3.png)
![]()
Plus généralement, pour tout vecteur ![]() on peut écrire :
on peut écrire :
![]()
![]()
En particulier :
![]()
Autrement dit :
Théorème (projection orthogonale sur un SEV de dimension finie)
Etant donnés :
- un espace préhilbertien
- un sous-espace vectoriel
 de dimension finie,
de dimension finie, - et un vecteur
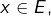
la distance de ![]() à un vecteur
à un vecteur ![]() (qui est mesurée par
(qui est mesurée par ![]() est minimale lorsque
est minimale lorsque ![]() est le projeté orthogonal de
est le projeté orthogonal de ![]() sur
sur ![]() En symboles :
En symboles :
![]()
En outre, si ![]() est une base orthonormale de
est une base orthonormale de ![]() alors :
alors :
![Rendered by QuickLaTeX.com \[\inf_{y\in F}\left\Vert x-y\right\Vert =\sqrt{\left\Vert x\right\Vert ^{2}-\left\Vert p_{F}\left(x\right)\right\Vert ^{2}}=\sqrt{\left\Vert x\right\Vert ^{2}-\sum_{i=1}^{r}\left(x\mid e_{i}\right)^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6652eb419373be773cb57e02cbe61113_l3.png)
Ce résultat est fondamental, car il permet de traiter certains problèmes de recherche de minimum.
Par exemple, le calcul de :
![]()
![Rendered by QuickLaTeX.com E=\mathbb{R}_{3}\left[X\right],](https://math-os.com/wp-content/ql-cache/quicklatex.com-f7b238d9454dc74a90dec8787afceaa7_l3.png) l’espace des polynômes de degré inférieur ou égal à 3,
l’espace des polynômes de degré inférieur ou égal à 3,- le produit scalaire défini sur
 par :
par :![Rendered by QuickLaTeX.com \[\forall\left(P,Q\right)\in E^{2},\thinspace\left(P\mid Q\right)=\int_{0}^{+\infty}P\left(t\right)Q\left(t\right)e^{-t}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-681e2f9a16ccf33ecc0a7c33e40796cf_l3.png)
- le sous-espace
![Rendered by QuickLaTeX.com F=\mathbb{R}_{2}\left[X\right],](https://math-os.com/wp-content/ql-cache/quicklatex.com-3309dca14da019a8222166ac70022835_l3.png)
- le polynôme
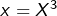
Ce calcul est traité en détail dans la fiche d’exercices n° 1 sur les produits scalaires (exercice n° 8).
4 – Orthogonal d’un hyperplan
Lorsque ![]() n’est plus supposé de dimension finie, la somme
n’est plus supposé de dimension finie, la somme ![]() est encore directe, car si un vecteur appartient à
est encore directe, car si un vecteur appartient à ![]() il est orthogonal à lui-même donc nul. Cependant, l’égalité
il est orthogonal à lui-même donc nul. Cependant, l’égalité ![]() n’est plus vraie en général.
n’est plus vraie en général.

Nous allons examiner cette situation dans le cas particulier où ![]() est un hyperplan de
est un hyperplan de ![]() (c’est-à-dire un sous-espace possédant une droite supplémentaire).
(c’est-à-dire un sous-espace possédant une droite supplémentaire).
Si ![]() est de dimension finie, alors d’après le théorème du supplémentaire orthogonal démontré à la section 2 :
est de dimension finie, alors d’après le théorème du supplémentaire orthogonal démontré à la section 2 :
![]()
Que se passe-t-il si ![]() est de dimension infinie ? La proposition suivante répond à cette question :
est de dimension infinie ? La proposition suivante répond à cette question :
Proposition 1
Pour tout hyperplan ![]() d’un espace préhilbertien
d’un espace préhilbertien ![]() de deux choses l’une :
de deux choses l’une :
- soit
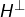 est une droite vectorielle,
est une droite vectorielle, - soit
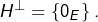
En effet, supposons que ![]() et soit
et soit ![]() Fatalement,
Fatalement, ![]() sans quoi
sans quoi ![]() serait orthogonal à lui-même donc nul.
serait orthogonal à lui-même donc nul.
Il en résulte que : ![]()
Avant de poursuivre, détaillons ce point …
On sait qu’il existe ![]() tel que
tel que ![]() En particulier, il existe
En particulier, il existe ![]() et
et ![]() tels que
tels que ![]() Nécessairement,
Nécessairement, ![]() car sinon
car sinon ![]() : contradiction ! On a donc :
: contradiction ! On a donc :
![]()
![]()
Terminons maintenant la preuve.
Comme ![]() il est clair que
il est clair que ![]()
Inversement, si ![]() alors en décomposant
alors en décomposant ![]() sous la forme
sous la forme ![]() avec
avec ![]() et
et ![]() on observe (en raison de la stabilité de
on observe (en raison de la stabilité de ![]() par combinaison linéaire) que :
par combinaison linéaire) que :
![]()
Finalement, si ![]() n’est pas réduit à
n’est pas réduit à ![]() c’est une droite vectorielle.
c’est une droite vectorielle.
La proposition 1 est démontrée.
Voyons maintenant deux exemples explicites, illustrant chacun l’une des deux possibilités.
On choisit pour ![]() l’espace vectoriel des applications continues de
l’espace vectoriel des applications continues de ![]() dans
dans ![]() que l’on munit du produit scalaire défini par :
que l’on munit du produit scalaire défini par :
![]()
Exemple 1 : un hyperplan dont l’orthogonal est nul
Considérons le sous-ensemble ![]() de
de ![]() constitué des applications qui s’annulent en
constitué des applications qui s’annulent en ![]()
![]() est le noyau de la forme linéaire non nulle
est le noyau de la forme linéaire non nulle ![]() C’est donc un hyperplan de
C’est donc un hyperplan de ![]()
Déterminons ![]()
Si ![]() alors :
alors :
![]()
On peut penser à choisir ![]() de la manière suivante : on fixe
de la manière suivante : on fixe ![]() assez proche de 0 et l’on considère l’application continue qui coïncide avec
assez proche de 0 et l’on considère l’application continue qui coïncide avec ![]() sur
sur ![]() et dont la restriction à
et dont la restriction à ![]() est linéaire. On ferait ensuite tendre
est linéaire. On ferait ensuite tendre ![]() vers
vers ![]() pour obtenir
pour obtenir ![]() et conclure ainsi que
et conclure ainsi que ![]()
Voyons une méthode moins géométrique… mais plus rapide (et qui sera généralisée à l’exercice n° 9 de cette fiche) !
Considérons l’application
![]()
![]()
L’application ![]() est continue, positive et d’intégrale nulle, donc identiquement nulle (si nécessaire, consulter le corrigé de l’exercice n° 6 de cette fiche).
est continue, positive et d’intégrale nulle, donc identiquement nulle (si nécessaire, consulter le corrigé de l’exercice n° 6 de cette fiche).
Ceci prouve que :
![]()
![]()
![]()
Mais comme ![]() est continue en
est continue en ![]() on a aussi :
on a aussi : ![]() Finalement,
Finalement, ![]() et l’on a prouvé que :
et l’on a prouvé que :
![]()
Exemple 2 : un hyperplan dont l’orthogonal est une droite
Considérons le sous-ensemble ![]() de
de ![]() constitué des applications dont l’intégrale sur
constitué des applications dont l’intégrale sur ![]() est nulle.
est nulle.
![]() est le noyau de la forme linéaire non nulle
est le noyau de la forme linéaire non nulle ![]() C’est donc un hyperplan de
C’est donc un hyperplan de ![]()
Déterminons ![]()
Si ![]() alors :
alors :
![]()
Choisissons pour ![]() l’élément de
l’élément de ![]() obtenu en retranchant à
obtenu en retranchant à ![]() sa valeur moyenne :
sa valeur moyenne :
![]()
On a donc :
![]()
![Rendered by QuickLaTeX.com \[ \int_{0}^{1}u\left(t\right)^{2}\thinspace dt=\left(\int_{0}^{1}u\left(t\right)\thinspace dt\right)^{2}\qquad\left(\spadesuit\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1370a8c3fc5241ca160b7c546ff5adb4_l3.png)
Arrêtons-nous un instant, car un rappel s’impose. Il s’agit de la célèbre …
Inégalité de Cauchy-Schwarz
Si ![]() est un espace préhilbertien, alors pour tout couple
est un espace préhilbertien, alors pour tout couple ![]() :
:
![]()
![]()
Dans le présent contexte, l’inégalité (CS) prend la forme suivante.
Pour tout couple ![]() d’applications continues de
d’applications continues de ![]() dans
dans ![]() :
:
![Rendered by QuickLaTeX.com \[ \left(\int_{0}^{1}f\left(t\right)g\left(t\right)\thinspace dt\right)^{2}\leqslant\left(\int_{0}^{1}f\left(t\right)^{2}\thinspace dt\right)\left(\int_{0}^{1}g\left(t\right)^{2}\thinspace dt\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b88265242041ee8e4d47b00d085d006c_l3.png)
On reconnait donc que ![]() correspond au cas d’égalité dans l’inégalité de Cauchy-Schwarz, pour le couple
correspond au cas d’égalité dans l’inégalité de Cauchy-Schwarz, pour le couple ![]() où
où ![]() désigne l’application constante
désigne l’application constante ![]()
Il est donc nécessaire que la famille ![]() soit liée, ce qui (vu que
soit liée, ce qui (vu que ![]() n’est pas l’application nulle) signifie qu’il existe
n’est pas l’application nulle) signifie qu’il existe ![]() tel que
tel que ![]()
Autrement dit, la condition ![]() signifie simplement que
signifie simplement que ![]() est constante.
est constante.
Réciproquement, il est facile de voir que toute application constante de ![]() dans
dans ![]() appartient à
appartient à ![]()
En définitive, ![]() est le sous-espace de
est le sous-espace de ![]() constitué des applications constantes, c’est-à-dire la droite vectorielle engendrée par
constitué des applications constantes, c’est-à-dire la droite vectorielle engendrée par ![]() :
:
![]()
5 – Bi-orthogonal d’un sous-espace
Par définition, étant donné un espace préhilbertien ![]() et une partie
et une partie ![]() de
de ![]() l’ensemble
l’ensemble ![]() sera appelé le bi-orthogonal de
sera appelé le bi-orthogonal de ![]() (je ne suis pas certain que cette appellation soit tout à fait standard, mais peu importe).
(je ne suis pas certain que cette appellation soit tout à fait standard, mais peu importe).
![]() est le sous-espace vectoriel formé des vecteurs qui sont orthogonaux à tous les éléments de
est le sous-espace vectoriel formé des vecteurs qui sont orthogonaux à tous les éléments de ![]() Il est donc évident que :
Il est donc évident que :
![]()
Dans le cas où ![]() est de dimension finie et si
est de dimension finie et si ![]() est un sous-espace vectoriel, on peut appliquer deux fois le théorème du supplémentaire orthogonal. D’une part :
est un sous-espace vectoriel, on peut appliquer deux fois le théorème du supplémentaire orthogonal. D’une part :
![]()
![]()
![]()
Avec une inclusion et l’égalité des dimensions, on conclut donc que :
Proposition 2
Si ![]() est un sous-espace vectoriel d’un espace euclidien, alors :
est un sous-espace vectoriel d’un espace euclidien, alors :
![]()
Maintenant, si ![]() est de dimension infinie, cette égalité n’est pas vraie en général. Il suffit pour le voir de considérer l’exemple 1 de la section précédente. On a vu en effet que l’hyperplan
est de dimension infinie, cette égalité n’est pas vraie en général. Il suffit pour le voir de considérer l’exemple 1 de la section précédente. On a vu en effet que l’hyperplan ![]() vérifiait
vérifiait ![]() Par conséquent :
Par conséquent :
![]()
Proposition 3
Si ![]() est un espace préhilbertien et si
est un espace préhilbertien et si ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() tel que
tel que ![]() alors
alors ![]()
Manifestement, la proposition 3 prolonge la 2. Mais pour l’établir, plus moyen de faire intervenir la notion de dimension …
Considérons ![]() et décomposons-le sous la forme
et décomposons-le sous la forme ![]() avec
avec ![]() et
et ![]()
Alors ![]() car
car ![]() et
et ![]() est stable par différence. Donc
est stable par différence. Donc ![]() et donc
et donc ![]() (vecteur orthogonal à lui-même, one more time …). Ceci prouve l’inclusion
(vecteur orthogonal à lui-même, one more time …). Ceci prouve l’inclusion ![]() et donc l’égalité. La proposition 3 est établie.
et donc l’égalité. La proposition 3 est établie.
Pour finir cette section, nous allons montrer que la réciproque de l’implication établie dans la proposition 3 est fausse. Il s’agit de trouver un exemple de sous-espace ![]() d’un espace préhilbertien
d’un espace préhilbertien ![]() vérifiant
vérifiant ![]() mais
mais ![]()
Exemple 3 : un sous-espace vérifiant 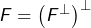 mais
mais 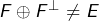
Soit ![]() l’espace des applications continues de
l’espace des applications continues de ![]() dans
dans ![]() muni du produit scalaire défini par :
muni du produit scalaire défini par :
![]()
![]()
![]()
Vérifions que ![]() et que
et que ![]() .
.
Il en résultera que :
![Rendered by QuickLaTeX.com \[\boxed{G=\left(G^{\bot}\right)^{\bot}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d91b5f2880a4c2d35ee9e2e751e099cc_l3.png)
![]()
Si ![]() considérons l’application
considérons l’application ![]() définie par :
définie par :
![Rendered by QuickLaTeX.com \[\forall t\in\left[-1,1\right],\thinspace g\left(t\right)=\left\{\begin{array}{cc}0 & \text{si }t\in\left[-1,0\right]\\\\t\thinspace f\left(t\right) & \text{si }t\in\left[0,1\right]\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c208160e5b8471545a285035e1b5195e_l3.png)
Visiblement, ![]() et donc
et donc ![]() c’est-à-dire :
c’est-à-dire :
![]()
Ceci entraîne que ![]() est nulle sur
est nulle sur ![]() autrement dit que
autrement dit que ![]() Ainsi,
Ainsi, ![]() et l’inclusion inverse est claire. Bref :
et l’inclusion inverse est claire. Bref :
![]()
![]()
6 – Sous-espaces fermés
Les pré-requis pour ce qui suit sont la notion de partie fermée d’un espace vectoriel normé et les trois propriétés suivantes :
- l’intersection de toute famille de fermés de
 est un fermé de
est un fermé de 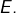
- si
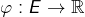 est une application continue, alors l’image réciproque par
est une application continue, alors l’image réciproque par 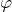 d’un fermé de
d’un fermé de  est un fermé de
est un fermé de 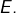
- une forme linéaire
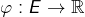 est continue si, et seulement s’il existe
est continue si, et seulement s’il existe 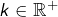 tel que
tel que![Rendered by QuickLaTeX.com \[\forall x\in E,\thinspace\left|\varphi\left(x\right)\right|\leqslant k\thinspace\left\Vert x\right\Vert\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-429db41113013e51975adc448d5cf437_l3.png)
Soit ![]() un espace préhilbertien. Pour tout
un espace préhilbertien. Pour tout ![]() notons
notons ![]() la forme linéaire définie par :
la forme linéaire définie par :
![]()
![]()
Pour toute partie ![]() de
de ![]() on constate avec la définition de l’orthogonal que :
on constate avec la définition de l’orthogonal que :
![]()
Ainsi, ![]() se présente comme l’intersection d’une famille de fermés et c’est donc un fermé de
se présente comme l’intersection d’une famille de fermés et c’est donc un fermé de ![]()
En particulier, si un sous-espace ![]() de
de ![]() vérifie
vérifie ![]() alors
alors ![]() est fermé dans
est fermé dans ![]() Nous allons maintenant voir, à l’aide d’un contre-exemple, que la réciproque est fausse.
Nous allons maintenant voir, à l’aide d’un contre-exemple, que la réciproque est fausse.
Exemple 4 : un sous-espace fermé qui ne coïncide pas avec son bi-orthogonal
On revient à l’espace ![]() des applications continues de
des applications continues de ![]() dans
dans ![]() muni du produit scalaire défini par :
muni du produit scalaire défini par :
![]()
![]()
![]() est un hyperplan car c’est le noyau de la forme linéaire non nulle
est un hyperplan car c’est le noyau de la forme linéaire non nulle ![]()
En outre ![]() est continue puisque, pour tout
est continue puisque, pour tout ![]() et d’après l’inégalité de Cauchy-Schwarz :
et d’après l’inégalité de Cauchy-Schwarz :
![Rendered by QuickLaTeX.com \[\left|\psi\left(f\right)\right|=\left|\int_{0}^{a}f\left(t\right)\thinspace dt\right|\leqslant\left(\int_{0}^{a}dt\right)^{1/2}\left(\int_{0}^{a}f\left(t\right)^{2}\thinspace dt\right)^{1/2}=\sqrt{a}\left\Vert f\right\Vert _{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cfeadf019fa3fea8402c2bf36a0609bb_l3.png)
Par conséquent, ![]() est fermé dans
est fermé dans ![]() Déterminons son orthogonal.
Déterminons son orthogonal.
Soit ![]() Pour tout
Pour tout ![]() considérons
considérons ![]() définie par :
définie par :
![]()
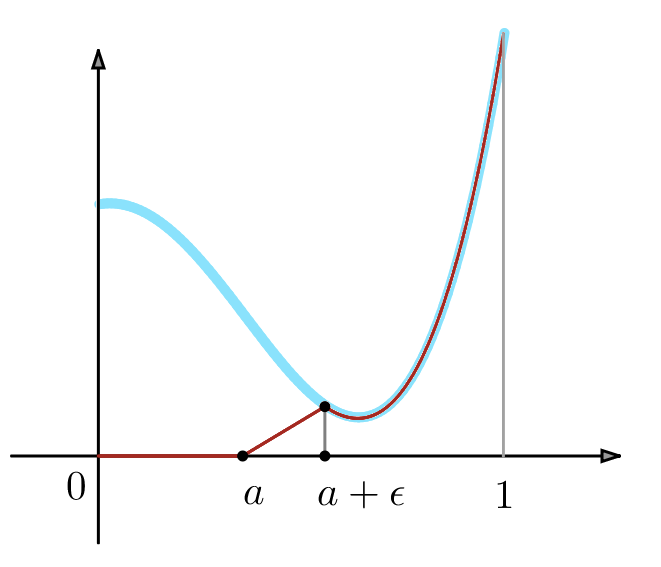
En bleu ciel, le graphe de ![]() , en rouge celui de
, en rouge celui de ![]()
Manifestement ![]() et donc :
et donc :
![]()
![]()
![]()
![]()
En passant à la limite dans ![]() on obtient donc
on obtient donc ![]() ce qui prouve que
ce qui prouve que ![]() est identiquement nulle sur
est identiquement nulle sur ![]()
Maintenant, notons ![]() et posons :
et posons :
![]()
Alors ![]() et donc
et donc ![]() c’est-à-dire :
c’est-à-dire :
![]()
![]()
On reconnaît (comme pour l’exemple 2 plus haut) le cas d’égalité dans l’inégalité de Cauchy-Schwarz, pour le couple formé par les restrictions à ![]() de
de ![]() et
et ![]() Ces restrictions sont donc linéairement dépendantes : autrement dit,
Ces restrictions sont donc linéairement dépendantes : autrement dit, ![]() est constante sur
est constante sur ![]()
Par continuité de ![]() en
en ![]() on voit que
on voit que ![]() , et finalement :
, et finalement :
![]()
En particulier : ![]()
7 – Un mot sur les espaces de Hilbert
Soit ![]() un espace vectoriel normé réel (pour ne pas sortir trop du contexte de cet article, on reste dans le champ réel, mais ce qui suit s’applique aussi bien aux espaces vectoriels normés sur le corps
un espace vectoriel normé réel (pour ne pas sortir trop du contexte de cet article, on reste dans le champ réel, mais ce qui suit s’applique aussi bien aux espaces vectoriels normés sur le corps ![]() des nombres complexes).
des nombres complexes).
La norme en vigueur sur ![]() sera notée
sera notée ![]()
Une suite ![]() de vecteurs de
de vecteurs de ![]() est dite convergente lorsqu’il existe un vecteur
est dite convergente lorsqu’il existe un vecteur ![]() tel que :
tel que :
![]()
![]()
Cette même suite est dite de Cauchy lorsque :
![]()
Il est facile de voir que toute suite convergente est de Cauchy, mais la réciproque est fausse en général.
Il existe cependant des espaces normés dans lesquels toute suite de Cauchy est convergente : ce sont les espaces normés complets, aussi appelés espaces de Banach, en l’honneur du mathématicien polonais Stefan BANACH (1892 – 1945).
Quant aux espaces préhilbertiens complets, ils sont appelés espaces de Hilbert, en l’honneur, cette fois, du mathématicien allemand David HILBERT (1862 – 1943).
Les espaces complets jouent un rôle très important en analyse. Sans entrer dans les détails, on peut dans un tel espace prouver la convergence d’une suite sans avoir la moindre idée de sa limite (en se contentant de vérifier le critère de Cauchy ![]() ci-dessus). Ceci explique en partie l’importance de cette notion.
ci-dessus). Ceci explique en partie l’importance de cette notion.
Pour en savoir plus sur les suites de Cauchy, on peut consulter cet article.
Nous avons vu, pour tout espace préhilbertien ![]() et tout sous-espace
et tout sous-espace ![]() les implications suivantes :
les implications suivantes :

Les réciproques des implications ![]() et
et ![]() sont fausses, comme l’ont montré l’exemple 3 et l’exemple 4 plus haut. Cependant, on a le :
sont fausses, comme l’ont montré l’exemple 3 et l’exemple 4 plus haut. Cependant, on a le :
Théorème
Si ![]() est un sous-espace fermé de l’espace de Hilbert
est un sous-espace fermé de l’espace de Hilbert ![]() , alors l’assertion
, alors l’assertion ![]() est vraie.
est vraie.
Les assertions ![]()
![]() et
et ![]() sont donc équivalentes dans le cas où
sont donc équivalentes dans le cas où ![]() est complet.
est complet.
Pour voir cela, on commence par établir le :
Théorème de la projection orthogonale
Soit ![]() un espace de Hilbert et soit
un espace de Hilbert et soit ![]() une partie non vide de
une partie non vide de ![]() convexe et fermée. Alors, pour tout
convexe et fermée. Alors, pour tout ![]() il existe un unique
il existe un unique ![]() tel que :
tel que :
![]()
![]()
➡ Vous trouverez une démonstration de ce résultat dans l’article consacré aux suites de Cauchy et aux espaces complets.
Bien entendu, tout sous-espace vectoriel d’un ![]() espace vectoriel est une partie non vide et convexe. Par conséquent, si
espace vectoriel est une partie non vide et convexe. Par conséquent, si ![]() est un sous-espace fermé d’un espace de Hilbert
est un sous-espace fermé d’un espace de Hilbert ![]() alors pour tout
alors pour tout ![]() le vecteur
le vecteur ![]() dont le théorème ci-dessus donne l’existence et l’unicité, vérifie pour tout
dont le théorème ci-dessus donne l’existence et l’unicité, vérifie pour tout ![]() et tout
et tout ![]() :
:
![]()
![]()
Il est clair que la somme ![]() est directe. On vient donc de montrer que
est directe. On vient donc de montrer que ![]() .
.
Le théorème du supplémentaire orthogonal pour un sous-espace fermé d’un espace de Hilbert est ainsi établi.
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.
