Neuf énoncés d’exercices de calcul intégral (fiche 04) : intégrales impropres.

Déterminer la nature de chacune des six intégrales impropres suivantes :
![Rendered by QuickLaTeX.com \[\begin{array}{ccc}{\displaystyle A=\int_{0}^{1}\frac{\ln\left(t\right)}{t-1}\thinspace dt} & ; & {\displaystyle B=\int_{0}^{+\infty}e^{-\sqrt{t}}\cos\left(t\right)\thinspace dt}\\\\\displaystyle{C=\int_{0}^{1}\frac{e^{t}-e}{\left(1-t\right)^2\sqrt t}\thinspace dt} & ; & {\displaystyle D=\int_{0}^{+\infty}\frac{\sin^{3}\left(t\right)}{t}\thinspace dt}\\\\{\displaystyle E=\int_{0}^{+\infty}}\cos\left(t\right)\arctan\left(\frac{1}{t}\right)\thinspace dt & & {\displaystyle F=\int_{-2}^{1}\frac{e^{t+2}-1}{\left(t^{3}+8\right)^{1/3}}\thinspace dt}\end{array}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e7792c3a6e565717b7e5c0c2b7b36924_l3.png)

Soit ![]() continue et possédant en
continue et possédant en ![]() une limite
une limite ![]() (finie ou infinie).
(finie ou infinie).
Montrer que si l’intégrale impropre ![]() converge, alors
converge, alors ![]()

Attention ! Cette intégrale peut très bien converger sans que ![]() n’admette de limite en
n’admette de limite en ![]()
Voir à ce sujet l’exercice n° 7 ci-dessous ou bien ici.

Montrer que, pour tout ![]() :
:
![]()

On considère, pour ![]() , les intégrales impropres (dites « de Bertrand ») :
, les intégrales impropres (dites « de Bertrand ») :
![Rendered by QuickLaTeX.com \[{\displaystyle \int_{a}^{+\infty}\frac{1}{t^{\alpha}\ln^{\beta}\left(t\right)}\thinspace dt}\qquad\text{avec }\left(\alpha,\beta\right)\in\mathbb{R}^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4f7b3792e529763a34fac6054981e82f_l3.png)
![]()
Ces intégrales doivent être considérées comme des « intégrales de référence ».

On pose, pour tout ![]() :
:
![]()

Montrer que pour tout ![]() et pour tout
et pour tout ![]() :
:
![]()
On pourra faire intervenir la suite des intégrales de Wallis (voir par exemple les premières sections de cet article).

Soit ![]() une suite décroissante à termes strictement positifs.
une suite décroissante à termes strictement positifs.
On suppose que ![]() et que la série
et que la série ![]() converge.
converge.
On définit alors une application ![]() de la manière suivante.
de la manière suivante.
Pour tout ![]() la restriction de
la restriction de ![]() à l’intervalle
à l’intervalle ![]() est définie par les conditions :
est définie par les conditions :
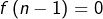
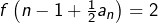
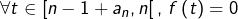
 affine sur
affine sur ![Rendered by QuickLaTeX.com \left[n-1,n-1+\frac{1}{2}a_{n}\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b75f63ebc9d28aac89e2498f05849a99_l3.png)
 affine sur
affine sur ![Rendered by QuickLaTeX.com \left[n-1+\frac{1}{2}a_{n},n-1+a_{n}\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6f9ed2333c0c1cee658c46feb1c70c57_l3.png)
Faire une figure, puis montrer que l’intégrale impropre ![]() converge mais que
converge mais que ![]() n’admet pas de limite en
n’admet pas de limite en ![]()
Cet exemple est à comparer avec celui donné dans cet article.

On pose, pour tout ![]() :
:
![]()
Pour la convergence de l’intégrale (doublement impropre) qui définit ![]() , voir par exemple ici.
, voir par exemple ici.

Soit ![]() logarithmiquement convexe (ce qui signifie que
logarithmiquement convexe (ce qui signifie que ![]() est convexe) et telle que :
est convexe) et telle que :
![Rendered by QuickLaTeX.com \[\left\{\begin{array}{c}f\left(1\right)=1\\\\\forall x>0,\,f\left(x+1\right)=x\,f\left(x\right)\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-aea7359ced99092dbbb6ded61d79502c_l3.png)
Montrer que
Cliquer ici pour accéder aux indications
Cliquer ici pour accéder aux solutions

