

Nature de six intégrales impropres
Pour 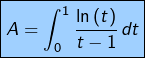
➢ En 0 :
![]()
➢ En 1 :
![]()
Ainsi, l’intégrale ![]() converge.
converge.
Pour 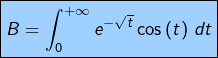
Pour tout ![]() :
:
![]()
![]()
![]()
Pour 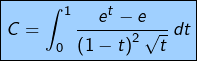
Inutile d’examiner ce qui se passe en la borne 0, vu ce qui suit …
➢ En 1 :
![]()
![]()
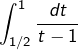 diverge.
diverge.
Pour 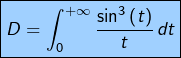
➢ En 0, on prolonge par continuité, vu que :
![]()
➢ Ensuite, on linéarise ![]() :
:
![]()
![]()
![]()
![]()
Pour 
➢ En 0 :
![]()
➢ En ![]() pas question d’utiliser la règle des équivalents car l’intégrande n’est pas de signe localement constant. En revanche :
pas question d’utiliser la règle des équivalents car l’intégrande n’est pas de signe localement constant. En revanche :
![]()
![]()
Finalement, l’intégrale ![]() converge.
converge.
Pour 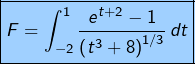
Si l’on pose ![]() alors :
alors :
![]()
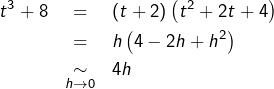
![Rendered by QuickLaTeX.com \[\frac{e^{t+2}-1}{\left(t^{3}+8\right)^{1/3}}\underset{{\scriptstyle -2}}{\sim}4^{-1/3}\thinspace\left(t+2\right)^{2/3}\underset{t\rightarrow-2}{\rightarrow}0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3c72d366c821900412811ef90c2ad50a_l3.png)
Ainsi, l’intégrale 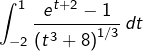 converge.
converge.

Supposons ![]() Il existe alors
Il existe alors ![]() tel que
tel que ![]() et donc :
et donc :
![]()
De même, en supposant que ![]() admet en
admet en ![]() une limite finie
une limite finie ![]() il existera
il existera ![]() tel que
tel que ![]() d’où :
d’où :
![]()
On voit de la même façon (ou bien en appliquant ce qui précède à ![]() que
que ![]() ne peut pas admettre pour limite
ne peut pas admettre pour limite ![]() en
en ![]() ni une limite finie strictement négative.
ni une limite finie strictement négative.
Il s’ensuit que, SI ![]() admet en
admet en ![]() une limite finie, celle-ci est nécessairement nulle.
une limite finie, celle-ci est nécessairement nulle.
Remarque – Comme cela a été indiqué dans l’énoncé, la convergence d’une telle intégrale impropre n’impose pas l’existence d’une limite pour ![]() en
en ![]() , voir l’exercice 7 de cette même fiche.
, voir l’exercice 7 de cette même fiche.

Etant donné ![]() la propriété des croissances comparées donne :
la propriété des croissances comparées donne :
![]()
![]()
L’intégrale impropre :
![]()
Fixons temporairement un réel ![]() notons pour tout
notons pour tout ![]() :
:
![]()
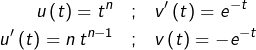
On obtient :
![]()
![]()
En passant à la limite dans cette égalité lorsque ![]() on obtient
on obtient ![]() Et vu que :
Et vu que :
![]()
![]()
Remarque
![]() est la valeur en
est la valeur en ![]() de la célèbre fonction Gamma d’Euler, définie sur
de la célèbre fonction Gamma d’Euler, définie sur ![]() par la formule :
par la formule :
![]()

Soient ![]() et
et ![]() On étudie la nature de l’intégrale impropre
On étudie la nature de l’intégrale impropre
![Rendered by QuickLaTeX.com \[{\displaystyle \int_{a}^{+\infty}\frac{1}{t^{\alpha}\ln^{\beta}\left(t\right)}\thinspace dt}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-23c52fa3cf7e195b27cb6cef94d160f8_l3.png)
➤ 1er cas : ![]()
Choisissons ![]() et observons que, pour tout
et observons que, pour tout ![]() :
:
(![]() )
) ![]()
![]()
![]()
![]()
➤ 2ème cas : ![]()
On choisit cette fois ![]() et vu que :
et vu que :
![]()
![]()
![]()
➤ 3ème cas : ![]()
On introduit, pour tout ![]() l’intégrale partielle :
l’intégrale partielle :
![]()
![Rendered by QuickLaTeX.com \[F\left(x\right)=\int_{\ln\left(a\right)}^{\ln\left(x\right)}\thinspace\frac{du}{u^{\beta}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1f31709fe4da3c40152b5cff2b35e385_l3.png)
Supposons dans un premier temps que ![]() Alors :
Alors :
![Rendered by QuickLaTeX.com \begin{eqnarray*}F\left(x\right) & = & \left[\frac{1}{\left(1-\beta\right)u^{\beta-1}}\right]_{u=\ln\left(a\right)}^{\ln\left(x\right)}\\ & = & \frac{1}{1-\beta}\left(\frac{1}{\ln^{\beta-1}\left(x\right)}-\frac{1}{\ln^{\beta-1}\left(a\right)}\right)\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-5ad1ce10f6cd361b39455e789bed2590_l3.png)
➣ Si ![]() alors :
alors :
![]()
![]()
➣ Si ![]() alors :
alors :
![]()
![]()
➣ Enfin si ![]() alors :
alors :
![]()
En conclusion
![Rendered by QuickLaTeX.com \[{\displaystyle \int_{a}^{+\infty}\frac{1}{t^{\alpha}\ln^{\beta}\left(t\right)}\thinspace dt}\;\text{converge}\Leftrightarrow\left\{\begin{array}{c}\alpha>1\\\text{ou}\\\alpha=1\text{ et }\beta>1\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d640cc9644b7b96e961a0b353f295c93_l3.png)

Commençons par le calcul de :
![]()
![]()
![]()
Le théorème de convergence dominée s’applique donc. On obtient :
![]()
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow+\infty}I_{n}=1-\frac{1}{e}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-04f0147a9a501b07c4c54b1b51366e7f_l3.png)
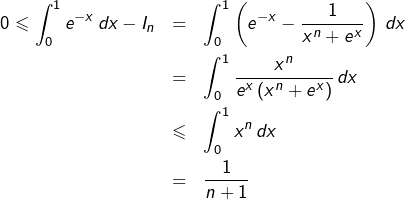
![]()
![]()
![]()
![]()
Il reste à préciser la nature de la série de terme général ![]() Bien entendu, le fait que la suite
Bien entendu, le fait que la suite ![]() converge vers 0 ne nous apprend rien à ce sujet … pas plus que la majoration obtenue plus haut (puisque la série harmonique est divergente).
converge vers 0 ne nous apprend rien à ce sujet … pas plus que la majoration obtenue plus haut (puisque la série harmonique est divergente).
En revanche, étant donné ![]() on observe que pour tout
on observe que pour tout ![]() :
:
![]()
![]()

On sait que, pour tout ![]() :
: ![]() Ceci se prouve directement en étudiant les variations de
Ceci se prouve directement en étudiant les variations de ![]()
On peut aussi remarquer que ![]() est la fonction affine tangente à l’exponentielle en 0; or l’exponentielle est convexe, donc minorée par chacune de ses fonctions affines tangentes.
est la fonction affine tangente à l’exponentielle en 0; or l’exponentielle est convexe, donc minorée par chacune de ses fonctions affines tangentes.
Il s’ensuit que, pour tout ![]() et pour tout
et pour tout ![]() :
:
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[e^{-t^{2}/n}\leqslant\left(1+\frac{t^{2}}{n}\right)^{-1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b1377b30ae6925cede96b194b1a85031_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\boxed{\forall n\in\mathbb{N}^{\star},\thinspace\forall t\in\left[0,\sqrt{n}\right],\thinspace\left(1-\frac{t^{2}}{n}\right)^{n}\leqslant e^{-t^{2}}\leqslant\left(1+\frac{t^{2}}{n}\right)^{-n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fc16346c89fdc2cc2bdc8e1b9858c691_l3.png)
Illustration dynamique pour cet encadrement
On peut voir ci-dessous les graphes des trois fonctions. Les unités ne sont pas identiques sur les axes de coordonnées. Le slider permet de faire varier ![]() et d’apprécier, à l’œil nu, la qualité de l’encadrement :
et d’apprécier, à l’œil nu, la qualité de l’encadrement :

D’après cet encadrement et par croissance de l’intégrale :
(![]() )
) ![]()
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{ccc}A_{n} & = & \int_{0}^{\sqrt{n}}\left(1-\frac{t^{2}}{n}\right)^{n}\thinspace dt\\\\B_{n} & = & \int_{0}^{\sqrt{n}}\left(1+\frac{t^{2}}{n}\right)^{-n}\thinspace dt\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5532c491e15552a1a50ca34f8205dfc5_l3.png)
Si l’on prouve que les suites ![]() et
et ![]() convergent vers une même limite
convergent vers une même limite ![]() il en résultera, d’après l’encadrement
il en résultera, d’après l’encadrement ![]() , que la suite de terme général :
, que la suite de terme général :
![]()
![]()
![]()
On sait que :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow\infty}\int_{0}^{\sqrt{n}}e^{-t^{2}}\thinspace dt=\frac{1}{2}\sqrt{\pi}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-246591a7747eaefa52a72d24d889769f_l3.png)
Il reste un mot à dire. L’intégrale impropre ![]() converge et donc, pour toute suite
converge et donc, pour toute suite ![]() à termes positifs qui diverge vers
à termes positifs qui diverge vers ![]() on a :
on a :
![]()
Ceci vaut en particulier pour ![]() En conclusion :
En conclusion :
![Rendered by QuickLaTeX.com \[\boxed{\int_{0}^{+\infty}e^{-t^{2}}\thinspace dt=\frac{1}{2}\sqrt{\pi}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d8c7db7f6e7087632b99b8a67c2bbddc_l3.png)
Cette intégrale, qui joue un rôle central (jeu de mot) en probabilités, est connue sous le nom d’intégrale de Gauss.

Voici à quoi ressemble le graphe de ![]() :
:
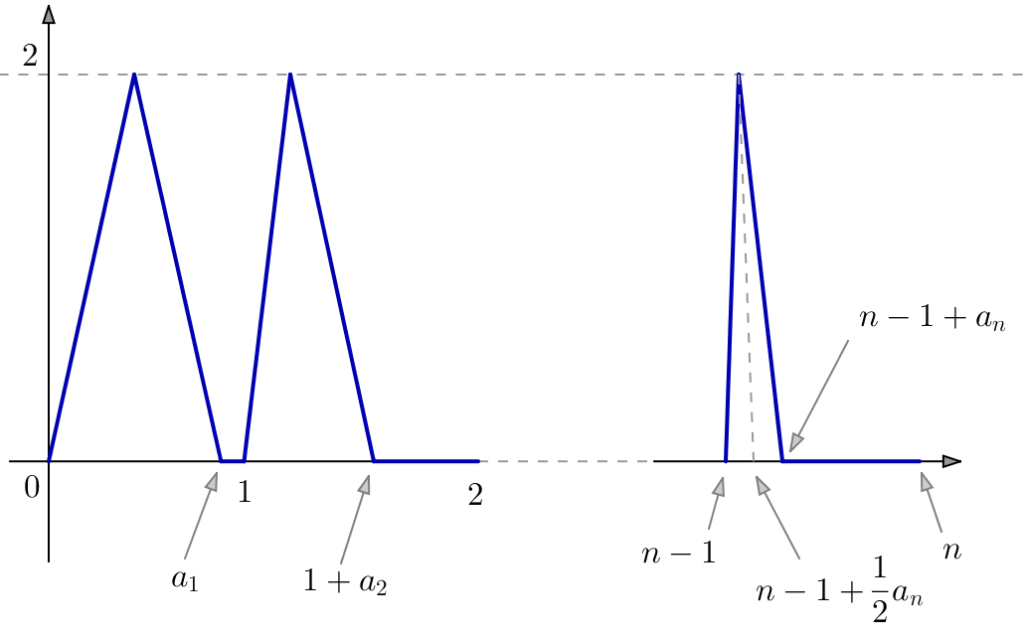
Posons, pour tout ![]() :
:
![]()
Comme ![]() est positive,
est positive, ![]() est croissante.
est croissante.
Pour tout ![]() on constate (aire d’un triangle de base
on constate (aire d’un triangle de base ![]() et de hauteur 2) que :
et de hauteur 2) que :
![]()
![Rendered by QuickLaTeX.com \[F\left(n\right)=\sum_{k=1}^{n}\int_{k-1}^{k}\thinspace f\left(t\right)\thinspace dt=\sum_{k=1}^{n}a_{k}\leqslant S\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-502d9b5b9d24d8150e89fec6bb20c186_l3.png)
![Rendered by QuickLaTeX.com \[S=\sum_{k=1}^{\infty}a_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7d63197833cc463277f9e5f64f576b4c_l3.png)
![]()
Pour finir, la suite ![]() converge vers 0 et la suite
converge vers 0 et la suite ![]() converge vers
converge vers ![]() (ces deux suites sont constantes !). Il en résulte que
(ces deux suites sont constantes !). Il en résulte que ![]() ne possède pas de limite en
ne possède pas de limite en ![]()

Commençons par préciser que, pour tout ![]() l’intégrale :
l’intégrale :
![]()
- d’une part, au voisinage de 0 :
et l’on sait que l’intégrale![Rendered by QuickLaTeX.com \[t^{x-1}e^{-t}\underset{{\scriptstyle 0}}{\sim}t^{x-1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bb7f4adf64fa839558bd68fc5c957242_l3.png)
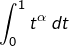 converge si, et seulement si,
converge si, et seulement si, 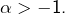
- d’autre part, au voisinage de
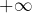 :
:
et donc, il existe![Rendered by QuickLaTeX.com \[\lim_{t\rightarrow+\infty}t^{x+1}e^{-t}=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-957e74f271772ec37198d6b0bc63d5b9_l3.png)
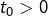 (qui dépend de
(qui dépend de 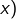 tel que :
tel que :![Rendered by QuickLaTeX.com \[\forall t\geqslant t_{0},\thinspace t^{x-1}e^{-t}\leqslant\frac{1}{t^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c659d3a66b003923256f7e71459155fa_l3.png)
Cela dit, on peut envisager deux méthodes pour établir la convexité de ![]()
➤ Méthode 1 : on dérive sous le signe ![]() (justification non détaillée ici) et l’on observe que :
(justification non détaillée ici) et l’on observe que :
![]()
➤ Méthode 2 (plus élémentaire mais aussi plus technique) : on revient à la définition de la convexité.
Détaillons la méthode 2. Fixons donc ![]() tels que
tels que ![]() ainsi que
ainsi que ![]() et montrons que
et montrons que
![]()
![]()
Pour la convexité de ![]() on dérive sous le signe
on dérive sous le signe ![]() Il s’agit de montrer que :
Il s’agit de montrer que :
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}\Gamma'\left(x\right)^{2} & = & \left(\int_{0}^{+\infty}\,\left[\ln\left(t\right)t^{\left(x-1\right)/2}e^{-t/2}\right]\,\left[t^{\left(x-1\right)/2}e^{-t/2}\right]\,dt\right)^{2}\\ & \leqslant & \left(\int_{0}^{+\infty}\,\ln^{2}\left(t\right)t^{x-1}e^{-t}\,dt\,dt\right)\left(\int_{0}^{+\infty}\,t^{x-1}e^{-t}\,dt\right)\\ & = & \Gamma''\left(x\right)\,\Gamma\left(x\right) \end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-7feaa1e01c40b612206ef76ed977d757_l3.png)

Comme ![]() est convexe, la comparaison des pentes sur les segments
est convexe, la comparaison des pentes sur les segments ![]() et
et ![]() donne pour tout
donne pour tout ![]() :
:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \ln\left(f\left(n+1\right)\right)-\ln\left(f\left(n\right)\right) & \leqslant & \frac{1}{x}\left[\ln\left(f\left(n+x+1\right)\right)-\ln\left(f\left(n+1\right)\right)\right]\\ & \leqslant & \ln\left(f\left(n+2\right)\right)-\ln\left(f\left(n+1\right)\right)\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-a9ff1a68a6b864d1bb9352c9f1ca177d_l3.png)
![]()
![]()
![]()
![]()
Compte tenu de la formule d’Euler, selon laquelle :
![]()
Vue l’équation fonctionnelle vérifiée par ![]() et
et ![]() , on conclut que
, on conclut que ![]()
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
