Neuf énoncés d’exercices sur la notion d’application (fiche 02).

Déterminer les triplets ![]() pour lesquels l’application
pour lesquels l’application
![]()

Soit ![]() une bijection. Montrer que :
une bijection. Montrer que :
- si
 est croissante alors
est croissante alors 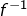 aussi.
aussi. - si
 est impaire alors
est impaire alors 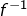 aussi.
aussi.

Soit E un ensemble fini de cardinal ![]()
Combien existe-t-il d’injections de ![]() dans E ?
dans E ?
Combien existe-t-il de surjections de E dans ![]() ?
?

Soient ![]() un ensemble et
un ensemble et ![]() une partie de
une partie de ![]()
On suppose que ![]() est injective. Peut-on affirmer que
est injective. Peut-on affirmer que ![]() est bijective ?
est bijective ?

On considère l’application :
![]()
- Montrer que
 est bijective et déterminer sa réciproque.
est bijective et déterminer sa réciproque. - Décrire géométriquement
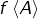 (l’image directe de
(l’image directe de 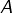 par
par  dans chacun des cas suivants :
dans chacun des cas suivants :

On considère l’application
![]()
Quelle est la bijection réciproque de ![]() ?
?

Prouver que l’application
![]()
Montrer ensuite que ![]() induit une bijection du disque unité ouvert
induit une bijection du disque unité ouvert ![]() sur le demi-plan ouvert
sur le demi-plan ouvert ![]()
Montrer que l’application
![]()
Trouver un équivalent de ![]() lorsque
lorsque ![]() et lorsque
et lorsque ![]()

Construire une bijection de ![]() sur
sur ![]()
Une telle bijection peut-elle être continue ? monotone ?
Cliquer ici pour accéder aux indications
Cliquer ici pour accéder aux solutions

