
Ce texte propose une présentation détaillée de la notion de continuité uniforme, pour une application à valeurs réelles, définie sur un intervalle de ![]() .
.
On y prouve notamment le théorème de Heine : toute application continue sur un segment, à valeurs réelles, est uniformément continue.
En guise d’application, on établit ensuite le théorème de Weierstrass trigonométrique, selon lequel toute application continue et ![]() périodique de
périodique de ![]() dans
dans ![]() est limite uniforme d’une suite de polynômes trigonométriques.
est limite uniforme d’une suite de polynômes trigonométriques.
Une assez bonne habitude de l’analyse réelle est requise, comme préalable à la lecture de cet article.
Dans ce qui suit, ![]() désigne un intervalle non trivial de
désigne un intervalle non trivial de ![]() (c’est-à-dire : ni vide, ni réduit à un singleton).
(c’est-à-dire : ni vide, ni réduit à un singleton).
1 – Lien avec la continuité ordinaire
Définition
Une application ![]() est dite uniformément continue lorsque :
est dite uniformément continue lorsque :
(![]() )
) ![]()
En substance, cette définition dit qu’on peut rendre l’écart entre ![]() et
et ![]() arbitrairement petit, pourvu que
arbitrairement petit, pourvu que ![]() et
et ![]() soient assez proches l’un de l’autre.
soient assez proches l’un de l’autre.
La différence entre la notion de continuité et celle de continuité uniforme ne saute peut-être pas aux yeux …
Comparons donc ![]() avec la définition formalisée de la continuité.
avec la définition formalisée de la continuité.
Rappelons que ![]() est dite continue sur
est dite continue sur ![]() si, et seulement si,
si, et seulement si, ![]() est continue en
est continue en ![]() pour tout
pour tout ![]() ce qui s’écrit :
ce qui s’écrit :
(![]() )
) ![]()
La différence formelle entre ![]() et
et ![]() consiste donc en la position d’un quantificateur universel :
consiste donc en la position d’un quantificateur universel :
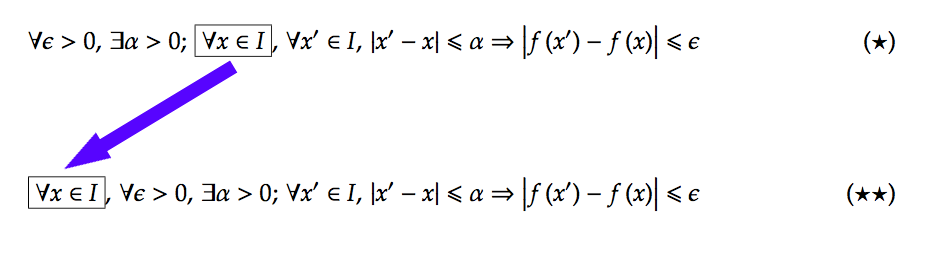
- Dans l’assertion
 ne dépend que de
ne dépend que de 
- Dans l’assertion
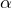 dépend a priori de
dépend a priori de  et de
et de 
On observe que, dans l’énoncé ![]() le nombre
le nombre ![]() convient à chaque
convient à chaque ![]() particulier, ce qui exprime une certaine uniformité, d’où la terminologie.
particulier, ce qui exprime une certaine uniformité, d’où la terminologie.
Les deux propositions suivantes sont évidentes (on désormais UC pour « uniformément continue ») :
Proposition 1
Soient ![]() deux intervalles tels que
deux intervalles tels que ![]() (avec
(avec ![]() non trivial).
non trivial).
Si ![]() est UC, alors la restriction de
est UC, alors la restriction de ![]() à
à ![]() est UC.
est UC.
Proposition 2
Toute application UC est continue.
Attention : la continuité n’implique pas la continuité uniforme !
Contre-Exemple 1
L’application ![]() (qui est continue puisque polynomiale) n’est pas UC.
(qui est continue puisque polynomiale) n’est pas UC.
Pour montrer cela, on s’assure que la négation de ![]() est vérifiée par
est vérifiée par ![]() c’est-à-dire que :
c’est-à-dire que :
![]()
Constatons que ![]() convient (tout
convient (tout ![]() ferait tout aussi bien l’affaire …). Pour tout
ferait tout aussi bien l’affaire …). Pour tout ![]() et pour tout
et pour tout ![]() :
:
![]()
![]()
C’était intuitivement clair : peu importe la valeur de ![]() on parvient toujours à rendre l’écart entre
on parvient toujours à rendre l’écart entre ![]() et
et ![]() plus grand que 1, en prenant
plus grand que 1, en prenant ![]() assez grand.
assez grand.
En revanche, si l’on considère plutôt
![]()
![]()
En effet, étant donné ![]() si l’on pose
si l’on pose ![]() alors pour tout
alors pour tout ![]() :
:
![]()
Généralisons ce qui vient d’être observé …
2 – Caractère lipschitzien et continuité uniforme
Définition
Une application ![]() est dite lipschitzienne lorsque l’ensemble des pentes des cordes de son graphe est borné.
est dite lipschitzienne lorsque l’ensemble des pentes des cordes de son graphe est borné.
Cela se traduit formellement par l’existence d’un réel ![]() tel que
tel que
(![]() )
) ![]()
On dit alors que ![]() est
est ![]() lipschitzienne ou bien qu’elle est lipschitzienne de rapport
lipschitzienne ou bien qu’elle est lipschitzienne de rapport ![]()
Proposition 3
Toute application lipschitzienne est UC.
Soit ![]() une application
une application ![]() lipschitzienne (avec
lipschitzienne (avec ![]() c’est-à-dire vérifiant
c’est-à-dire vérifiant ![]()
Etant donné ![]() si l’on pose
si l’on pose ![]() alors pour tout
alors pour tout ![]() vérifiant
vérifiant ![]() :
:
![]()
Corollaire
Toute application dérivable, dont la dérivée est bornée, est UC.
L’hypothèse entraîne en effet, d’après la formule des accroissements finis, que ![]() est lipschitzienne.
est lipschitzienne.
En particulier, si ![]() est un segment et si
est un segment et si ![]() est de classe
est de classe ![]() alors
alors ![]() est bornée (application continue sur un segment) et donc
est bornée (application continue sur un segment) et donc ![]() est UC d’après ce corollaire.
est UC d’après ce corollaire.
Bien entendu, pas de réciproque pour le corollaire puisqu’une application UC n’a aucune raison d’être dérivable (penser par exemple à la valeur absolue).
Pour finir, la réciproque de l’implication énoncée à la proposition 3 est fausse. En effet :
Contre-Exemple 2
L’application ![]() n’est pas lipschitzienne puisque, pour tout
n’est pas lipschitzienne puisque, pour tout ![]() :
:
![]()
Elle est pourtant UC. Pour le voir, montrons d’abord que :
(![]() )
) ![]()
Il suffit de traiter le cas où ![]() pour lequel on constate que :
pour lequel on constate que :
Maintenant, fixons ![]() et choisissons
et choisissons ![]()
On voit que, pour tout ![]() vérifiant
vérifiant ![]() :
:
![]()
Schématiquement, nous avons vu à ce stade que :
![]()
Le sigle DDB signifiant « dérivable à dérivée bornée ».
3 – Le théorème de Heine
Nous avons vu plus haut un exemple d’application continue mais non UC sur un intervalle ![]() (il s’agissait de
(il s’agissait de ![]()
Dans le cas où ![]() est un intervalle compact (c’est-à-dire un segment : intervalle de la forme
est un intervalle compact (c’est-à-dire un segment : intervalle de la forme ![]() avec
avec ![]() il se passe quelque chose de très spécial …
il se passe quelque chose de très spécial …
Théorème (HEINE)
Si ![]() est un segment et si
est un segment et si ![]() est continue, alors
est continue, alors ![]() est UC.
est UC.

La démonstration qui suit repose essentiellement sur le théorème de Bolzano-Weierstrass (selon lequel on peut, de toute suite réelle bornée, extraire une sous-suite convergente). Ce résultat est admis ici (pour une preuve courte voir l’exercice n° 9 de cette fiche ou encore consulter le lexique).
Preuve (cliquer pour déplier / replier)
Supposons ![]() non uniformément continue. Il existe donc
non uniformément continue. Il existe donc ![]() tel que :
tel que :
![]()
En choisissant ![]() (pour tout
(pour tout ![]() on peut construire deux suites
on peut construire deux suites ![]() et
et ![]() à termes dans
à termes dans ![]() vérifiant :
vérifiant :
![]()
D’après Bolzano-Weierstrass, il existe une suite ![]() extraite de
extraite de ![]() qui converge vers un élément
qui converge vers un élément ![]() de
de ![]() La relation :
La relation :
![]()
La continuité de ![]() en
en ![]() entraîne alors la convergence de chacune des suites
entraîne alors la convergence de chacune des suites ![]() et
et ![]() vers
vers ![]()
Par conséquent, dès que ![]() est assez grand :
est assez grand :
![]()
Les applications du théorème de Heine ne manquent pas.
Je vous en propose trois : les deux premières sont anecdotiques (ce sont, au mieux, des exercices intéressants), tandis que la troisième constitue un résultat significatif (et joue notamment un rôle en théorie des séries de Fourier).
Vous trouverez une autre application du théorème de Heine dans cet article.
4 – Deux exercices sympathiques
Exercice 1
Montrer que si ![]() est continue, alors
est continue, alors ![]() est « presque » lipschitzienne, au sens suivant :
est « presque » lipschitzienne, au sens suivant :
![]()
Solution proposée pour l’ex. 1 (cliquer pour déplier / replier)
Soit ![]() D’après le théorème de Heine, il existe
D’après le théorème de Heine, il existe ![]() tel que :
tel que :
![]()
Par ailleurs, ![]() est bornée (car continue sur un segment) :
est bornée (car continue sur un segment) :
![]()
![]()
Finalement, en posant ![]() on voit que pour tout
on voit que pour tout ![]() :
:
![]()
Exercice 2
Montrer que si ![]() est continue et admet une limite finie en
est continue et admet une limite finie en ![]() alors
alors ![]() est UC.
est UC.
Solution proposée pour l’ex. 2 (cliquer pour déplier / replier)
Notons ![]() la limite de
la limite de ![]() en
en ![]()
Nous allons prouver qu’étant donné ![]() l’écart
l’écart ![]() pourra être rendu inférieur à
pourra être rendu inférieur à ![]() dès que
dès que ![]() sont assez proches.
sont assez proches.
Par définition d’une limite, il existe ![]() tel que :
tel que :
![]()
Soit maintenant ![]()
Envisageons trois cas selon que :
 et
et  appartiennent à
appartiennent à 
 et
et 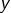 appartiennent à
appartiennent à ![Rendered by QuickLaTeX.com \left[a,A\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ae7af49ec22d28e49eeaea0aaf31abd0_l3.png)
 et
et 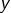 se situent de part et d’autre de
se situent de part et d’autre de 
D’après l’inégalité triangulaire :
(![]() )
) ![]()
D’après le théorème de Heine, ![]() est uniformément continue sur
est uniformément continue sur ![]() Il existe donc
Il existe donc ![]() tel que :
tel que :
(![]() )
) ![]()
Enfin, si ![]() et
et ![]() alors d’une part
alors d’une part ![]() d’où
d’où ![]() d’après
d’après ![]() et d’autre part
et d’autre part ![]() d’après
d’après ![]() . Donc :
. Donc :
![]()
On a montré que :
![]()
Noter que la réciproque de l’implication établie à l’exercice 2 est fausse.
Il existe en effet des applications ![]() uniformément continues et admettant une limite infinie en
uniformément continues et admettant une limite infinie en ![]() (il suffit de considérer
(il suffit de considérer ![]() ).
).
Il en existe même n’admettant pas de limite du tout en ![]() …!
…!
Exemple
Considérons l’application :
![]()
- d’une part, comme
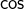 est
est 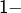 lipschitzienne et d’après une inégalité établie plus haut (pour la racine carrée) :
lipschitzienne et d’après une inégalité établie plus haut (pour la racine carrée) :
ce qui montre que![Rendered by QuickLaTeX.com \[\left|\cos\left(\sqrt{x}\right)-\cos\left(\sqrt{y}\right)\right|\leqslant\left|\sqrt{x}-\sqrt{y}\right|\leqslant\sqrt{\left|x-y\right|}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-868ed7de8ccf23dedb56345cbd746e84_l3.png)
 est UC.
est UC. - d’autre part, la suite
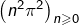 diverge vers
diverge vers 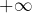 alors que
alors que 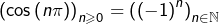 n’admet pas de limite. Par conséquent
n’admet pas de limite. Par conséquent  ne possède pas de limite en
ne possède pas de limite en 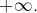
5 – Le théorème de Weierstrass trigonométrique
Soit ![]() l’espace vectoriel des applications continues et
l’espace vectoriel des applications continues et ![]() périodiques de
périodiques de ![]() dans
dans ![]()
On munit ![]() de la norme de la convergence uniforme :
de la norme de la convergence uniforme :
![]()
Noter, si ![]() est un segment de longueur
est un segment de longueur ![]() alors en raison de la
alors en raison de la ![]() périodicité :
périodicité :
![]()
Pour tout ![]() on note
on note ![]() et
et ![]() les applications respectivement définies par :
les applications respectivement définies par :
![]()
Pour tout ![]() on désigne par
on désigne par ![]() le sous-espace de
le sous-espace de ![]() engendré par la famille
engendré par la famille ![]() On note aussi
On note aussi ![]() le sous-espace constitué des applications constantes.
le sous-espace constitué des applications constantes.
Comme ![]() est une famille croissante pour l’inclusion, l’ensemble
est une famille croissante pour l’inclusion, l’ensemble ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() Ses éléments sont appelés « polynômes trigonométriques ».
Ses éléments sont appelés « polynômes trigonométriques ».
On établit maintenant le :
Théorème (WEIERSTRASS, version trigonométrique)
![]() est une partie dense de
est une partie dense de ![]()
Autrement dit, toute application ![]() continue et
continue et ![]() périodique est limite uniforme sur
périodique est limite uniforme sur ![]() (ou, ce qui revient au même, sur
(ou, ce qui revient au même, sur ![]() d’une suite de polynômes trigonométriques.
d’une suite de polynômes trigonométriques.
On va prouver ce résultat en définissant une suite ![]() par :
par :
![]()
On dit que ![]() est le produit de convolution de
est le produit de convolution de ![]() par
par ![]() .
.
On constatera que :
- chaque
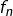 est un polynôme trigonométrique,
est un polynôme trigonométrique, - la suite
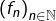 converge uniformément sur
converge uniformément sur  vers
vers 
ce qui donnera la conclusion. Voyons maintenant les choses de plus près…
Preuve détaillée du théorème (cliquer pour déplier / replier)
On commence par construire les 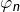 . (cliquer pour déplier / replier)
. (cliquer pour déplier / replier)
L’idée est qu’élevant à une grande puissance la restriction à ![]() de
de ![]() , on obtient quelque chose comme ceci :
, on obtient quelque chose comme ceci :
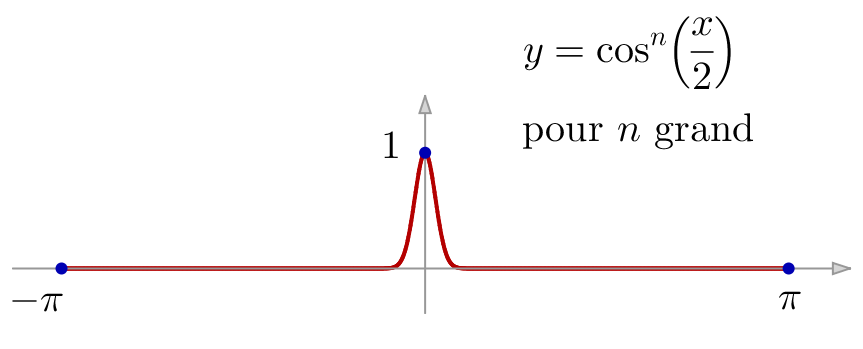
Il faut ensuite « normer », c’est-à-dire multiplier chaque fonction par un coefficient convenable, afin de forcer l’intégrale à valoir 1.
Posons donc , pour tout ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[\boxed{\int_{-\pi}^{\pi}\varphi_{n}\left(t\right)\thinspace dt=1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-640fc69c35c9a759f40d3699e485a9e4_l3.png)
Pour tout ![]() :
:
![]()
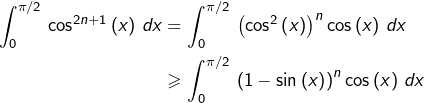
En posant ![]() dans cette dernière intégrale, il vient :
dans cette dernière intégrale, il vient :
![]()
On voit donc que :
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{K_{n}\leqslant\frac{n+1}{4}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-94d9144a89d19c954619fcd2ff6dba05_l3.png)
Soit maintenant ![]() Comme
Comme ![]() décroît sur
décroît sur ![]() alors pour tout
alors pour tout ![]() :
:
![]()
Ce dernier majorant est indépendant de ![]() donc :
donc :
![]()
Or, par croissances comparées :
![]()
![]()
Ensuite, cela ne saute pas aux yeux, mais :
Les  sont des polynômes trigonométriques (cliquer pour déplier / replier)
sont des polynômes trigonométriques (cliquer pour déplier / replier)
Pour le voir, on se sert de la formule d’Euler pour le cosinus et de la formule du binôme afin de linéariser l’expression ![]()
Pour tout ![]() :
:
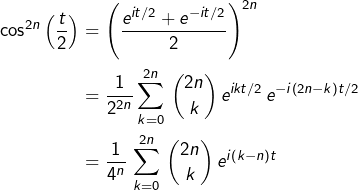
Cette quantité étant réelle, elle est égale à sa partie réelle :
![Rendered by QuickLaTeX.com \[\cos^{2n}\left(\frac{t}{2}\right)=\frac{1}{4^{n}}\,\sum_{k=0}^{2n}\,\binom{2n}{k}\,\cos\left(\left(k-n\right)t\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ed766f057724bfc062d03dd89ff6ef85_l3.png)
En isolant le terme central, puis en séparant en deux la somme restante, il vient :
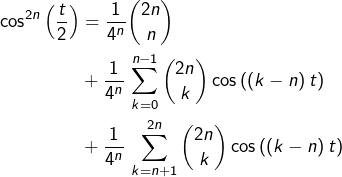
En multipliant par ![]() en ré-indexant les deux sommes puis en regroupant :
en ré-indexant les deux sommes puis en regroupant :
![Rendered by QuickLaTeX.com \[\varphi_{n}\left(t\right) & = & \frac{K_{n}}{4^{n}}\left[\binom{2n}{n}+\sum_{k=1}^{n}\left(\binom{2n}{n-k}+\binom{2n}{n+k}\right)\cos\left(kt\right)\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a2458912528ec497c3853cd4c9738cd3_l3.png)
Comme ceci vaut pour tout ![]() on en déduit que :
on en déduit que :
![Rendered by QuickLaTeX.com \[\varphi_{n}=\frac{K_{n}}{4^{n}}\left[\binom{2n}{n}c_{0}+\sum_{k=1}^{n}\left(\binom{2n}{n-k}+\binom{2n}{n+k}\right)c_{k}\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e0a84613d0a7f04bc6ad1436cfd4628b_l3.png)
Posons ensuite, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\boxed{f_{n}\left(x\right)={\displaystyle \int_{-\pi}^{\pi}f\left(x-t\right)\thinspace\varphi_{n}\left(t\right)\,dt}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e9aa257ec8479ca6fdba3be4f6fce87c_l3.png)
On constate alors que :
Chaque 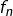 est un polynôme trigonométrique (cliquer pour déplier / replier)
est un polynôme trigonométrique (cliquer pour déplier / replier)
En effet, en posant ![]() dans l’intégrale précédente, on voit que :
dans l’intégrale précédente, on voit que :
![]()
Comme l’application ![]() est
est ![]() périodique, son intégrale sur un segment de longueur
périodique, son intégrale sur un segment de longueur ![]() ne dépend pas du segment choisi. Ainsi :
ne dépend pas du segment choisi. Ainsi :
![]()
Par ailleurs, on a vu qu’il existe des réels ![]() tels que :
tels que :
![Rendered by QuickLaTeX.com \[\forall t\in\mathbb{R},\,\varphi_{n}\left(t\right)=\sum_{k=0}^{n}\,\lambda_{k}\,\cos\left(kt\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ed234f0fa18b2d45b780734ae61935ef_l3.png)
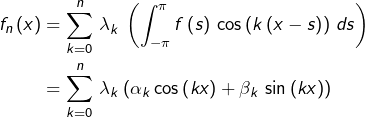
![]()
Manifestement : ![]()
La suite  converge uniformément sur
converge uniformément sur  vers
vers  (cliquer pour déplier / replier)
(cliquer pour déplier / replier)
Ensuite, comme ![]() on peut écrire artificiellement la différence
on peut écrire artificiellement la différence ![]() sous la forme :
sous la forme :
![]()
Posons :
![Rendered by QuickLaTeX.com \[\left\{\begin{array}{ccc}A_{n}\left(x\right) & = & \int_{-\pi}^{-\delta}\left(f\left(x\right)-f\left(x-t\right)\right)\,\varphi_{n}\left(t\right)\,dt+\int_{\delta}^{\pi}\left(f\left(x\right)-f\left(x-t\right)\right)\,\varphi_{n}\left(t\right)\,dt\\\\B_{n}\left(x\right) & = & \int_{-\delta}^{\delta}\left(f\left(x\right)-f\left(x-t\right)\right)\,\varphi_{n}\left(t\right)\,dt\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-58160adbcfed5f8668c7a6f6ec0c6c94_l3.png)
![]()
Pour tout ![]() on a d’une part :
on a d’une part :
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\left|A_{n}\left(x\right)\right| & \leqslant 2\,\left\Vert f\right\Vert_{\infty}\,\left(\int_{-\pi}^{-\delta}\,\varphi_{n}\left(t\right)\,dt+\int_{\delta}^{\pi}\,\varphi_{n}\left(t\right)\,dt\right)\\& \leqslant 4\,\left\Vert f\right\Vert_{\infty}\,\left(\pi-\delta\right)\,\sup_{t\in\left[\delta,\pi\right]}\varphi_{n}\left(t\right)\qquad\textrm{(car }\varphi_{n}\textrm{ est paire)}\\& \leqslant 4\pi\,\left\Vert f\right\Vert {\infty}\,\sup{t\in\left[\delta,\pi\right]}\varphi_{n}\left(t\right)\end{split}\end{equation*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-1263727b9b6b3cc35c874cdc21bee47a_l3.png)
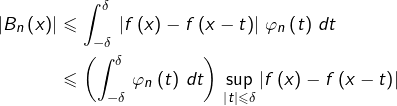
Ainsi, d’après l’inégalité triangulaire :
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\left|f\left(x\right)-f_{n}\left(x\right)\right| & \leqslant \left|A_{n}\left(x\right)\right|+\left|B_{n}\left(x\right)\right|\\& \leqslant 4\pi\,\left\Vert f\right\Vert_{\infty}\,\sup_{t\in\left[\delta,\pi\right]}\varphi_{n}\left(t\right)+\sup_{\left|t\right|\leqslant\delta}\left|f\left(u\right)-f\left(u-t\right)\right|\end{split}\end{equation*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-46089c88a1270ebd9b9844659a0a6f12_l3.png)
Or ![]() et donc :
et donc :
![]()
D’après le théorème de Heine, il existe, étant donné ![]() un réel
un réel ![]() tel que :
tel que :
![]()
Par ailleurs, d’après ![]() , il existe
, il existe ![]() tel que, pour tout entier
tel que, pour tout entier ![]() :
:
![]()
Noter que cette affirmation suppose ![]() non identiquement nulle (mais ce qu’il faut prouver est évident pour la fonction nulle !).
non identiquement nulle (mais ce qu’il faut prouver est évident pour la fonction nulle !).
On voit finalement que :
![]()
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.
