![]()

Nous allons examiner quelques unes des nombreuses propriétés de cette suite d’entiers, en commençant par ce qu’il y a de plus simple : la parité.
1 – Parité des coefficients binomiaux centraux
Rappelons la formule de Pascal. Pour tout couple d’entiers ![]() tel que
tel que ![]() :
:
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\forall n\in\mathbb{N}^{\star},\quad\binom{2n}{n}=2\thinspace\binom{2n-1}{n}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3b07c6c2de3cd673cf994b6456e92408_l3.png)
Remarque
2 – Un résultat plus précis
Intéressons-nous, pour tout ![]() à l’exposant de
à l’exposant de ![]() dans la décomposition en facteurs premiers de
dans la décomposition en facteurs premiers de ![]() Notons
Notons ![]() cet entier. Nous venons de voir que
cet entier. Nous venons de voir que ![]() mais il est naturel de se demander s’il est possible de calculer explicitement
mais il est naturel de se demander s’il est possible de calculer explicitement ![]()
Pour cela, nous allons utiliser la formule de Legendre (dont une preuve détaillée est disponible dans l’annexe de cet article). Rappelons de quoi il s’agit :
Formule de Legendre / Version 1
Pour tout entier ![]() et tout nombre premier
et tout nombre premier ![]() l’exposant de
l’exposant de ![]() dans la décomposition en facteurs premiers de
dans la décomposition en facteurs premiers de ![]() est donné par :
est donné par :
![Rendered by QuickLaTeX.com \[v_{p}\left(n!\right)=\sum_{i=1}^{n}\left\lfloor \frac{n}{p^{i}}\right\rfloor\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c8d0de434e6ab1a3910a8fb9f532c3b9_l3.png)
Dans cette formule, ![]() désigne la partie entière du réel
désigne la partie entière du réel ![]() C’est ainsi que, par exemple, l’exposant de
C’est ainsi que, par exemple, l’exposant de ![]() dans la décomposition en facteurs premiers de
dans la décomposition en facteurs premiers de ![]() est :
est :
![]()
![]()
Comme la valuation ![]() adique est additive (ce qui veut simplement dire que
adique est additive (ce qui veut simplement dire que ![]() pour tout couple
pour tout couple ![]() d’entiers naturels non nuls), on voit que :
d’entiers naturels non nuls), on voit que :
![]()
Formule de Legendre / Version 2
Pour tout entier ![]() et tout nombre premier
et tout nombre premier ![]() :
:
![]()
Si la notion d’écriture en base ![]() n’est pas claire pour vous, surtout pas de panique !… Tout est expliqué dans ces deux vidéos :
n’est pas claire pour vous, surtout pas de panique !… Tout est expliqué dans ces deux vidéos :


Quant à la preuve de cette seconde version de la formule de Legendre, les curieux la trouveront à l’annexe 1.
Avec ce nouvel outil, on constate que :
![]()
![]()
![]()
Théorème
Pour tout entier ![]() l’exposant de 2 dans la décomposition en facteurs premiers de
l’exposant de 2 dans la décomposition en facteurs premiers de ![]() est donné par le nombre de 1 dans l’écriture binaire de
est donné par le nombre de 1 dans l’écriture binaire de ![]()
On notera que le nombre de 1 dans l’écriture binaire de ![]() est évidemment égal à la somme des chiffres binaires de
est évidemment égal à la somme des chiffres binaires de ![]()
Un exemple, juste pour voir … Choisissons ![]() On calcule :
On calcule :
![]()
![]()
de
![]()
![]()
Corollaire
3 – Quatre formules pour le n-ème coefficient binomial central
(![]() )
) ![Rendered by QuickLaTeX.com \[\binom{2n}{n}=\sum_{k=0}^{n}\binom{n}{k}^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-502d1336c2b080a434f9c6b2533191c6_l3.png)
(![]() )
) ![Rendered by QuickLaTeX.com \[\binom{2n}{n}=\sum_{k=0}^{n}\left(-1\right)^{n-k}\binom{2n+1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a1609d8dc0a3d890991227ea5664973c_l3.png)
(![]() )
) ![Rendered by QuickLaTeX.com \[\binom{2n}{n}=\sum_{k=0}^{2n}\left(-1\right)^{n-k}\binom{2n}{k}^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-142271ce5519c6fd4451df6856412710_l3.png)
(![]() )
) ![Rendered by QuickLaTeX.com \[\binom{2n}{n}=\sum_{j=0}^{\left\lfloor n/2\right\rfloor }\binom{n}{j}\binom{n-j}{n-2j}2^{n-2j}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2bc6623c654c13f9a0f4937ce013890e_l3.png)
Cette courte liste n’a évidemment rien d’exhaustif ! Il existe une foule de formules donnant une expression plus ou moins exotique du ![]() ème coefficient binomial central.
ème coefficient binomial central.
Preuve de la formule n° 1
D’après la formule du binôme, l’entier ![]() s’interprète naturellement comme le coefficient de
s’interprète naturellement comme le coefficient de ![]() dans l’expression développée du polynôme
dans l’expression développée du polynôme ![]() Par ailleurs :
Par ailleurs :
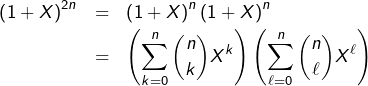
![Rendered by QuickLaTeX.com \[\binom{2n}{n}=\sum_{k=0}^{n}\binom{n}{k}\binom{n}{n-k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6c0372ae0da93ea0867aa62eda986918_l3.png)
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\binom{2n}{n}=\sum_{k=0}^{n}\binom{n}{k}^{2}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ae37d02cf7fba012aa4a4090d79f9ae1_l3.png)
Preuve de la formule n° 2
Cette question a fait l’objet du challenge 75. Le lecteur est prié de s’y reporter.
Preuve de la formule n° 3
Cette question est traitée dans cette vidéo (en anglais 🇺🇸🇬🇧) :
Mais donnons tout de même une preuve détaillée (en français 🙂)…
Pour tout ![]() notons
notons ![]() le coefficient de
le coefficient de ![]() dans l’expression développée du polynôme :
dans l’expression développée du polynôme :
![]()
![Rendered by QuickLaTeX.com \[P_{n}=\sum_{k=0}^{2n}\left(-1\right)^{k}\binom{2n}{k}X^{2k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a9c9446dadd21e2ef91597319c8d8514_l3.png)
![Rendered by QuickLaTeX.com \[\lambda_{n}=\left\{\begin{array}{cc}0 & \text{si }n\text{ est impair}\\\left(-1\right)^{n/2}{\displaystyle \binom{n}{n/2}} & \text{sinon}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-800ca317936b18ee4b08185a4175b369_l3.png)
![Rendered by QuickLaTeX.com \[P_{n}=\left(1-X\right)^{n}\left(1+X\right)^{n}=\left(\sum_{k=0}^{n}\left(-1\right)^{k}\binom{n}{k}X^{k}\right)\left(\sum_{\ell=0}^{n}\binom{n}{\ell}X^{\ell}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-894ff7311e67428428fc09fa02c106e3_l3.png)
![Rendered by QuickLaTeX.com \[\lambda_{n}=\sum_{k=0}^{n}\left(-1\right)^{k}\binom{n}{k}\binom{n}{n-k}=\sum_{k=0}^{n}\left(-1\right)^{k}\binom{n}{k}^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ac55701909c3fa27f3815f7ac25948a7_l3.png)
![Rendered by QuickLaTeX.com \[\left(-1\right)^{n}\binom{2n}{n}=\sum_{k=0}^{2n}\left(-1\right)^{k}\binom{2n}{k}^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-934eed61b63f2e98e296e21f37714ef7_l3.png)
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\binom{2n}{n}=\sum_{k=0}^{2n}\left(-1\right)^{n-k}\binom{2n}{k}^{2}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4a80ce08f32e88170bee9af5a821a575_l3.png)
Preuve de la formule n° 4
![]()
![Rendered by QuickLaTeX.com \[Q_{n}=\sum_{k=0}^{2n}\binom{2n}{k}X^{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-606418794a69c1af4f0d57cc2d5f349f_l3.png)
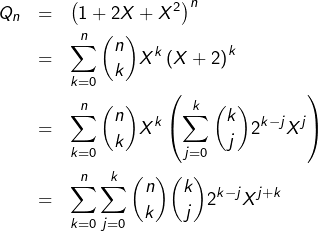
![]()
![Rendered by QuickLaTeX.com \[Q_{n}=\sum_{j=0}^{n}\sum_{k=j}^{n}\binom{n}{j}\binom{n-j}{k-j}2^{k-j}X^{j+k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-aa26ead1769166d68131e3dc3be5699b_l3.png)
![Rendered by QuickLaTeX.com \[Q_{n}=\sum_{j=0}^{n}\sum_{\ell=2j}^{n+j}\binom{n}{j}\binom{n-j}{\ell-2j}2^{\ell-2j}X^{\ell}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-715f238178cb586526a57d1a3db564bc_l3.png)
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\binom{2n}{n}=\sum_{j=0}^{\left\lfloor n/2\right\rfloor }\binom{n}{j}\binom{n-j}{n-2j}2^{n-2j}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6b50bc087db84b4d70ffcfc22dcdecdd_l3.png)
Remarque
Cette dernière formule redonne (mais d’une manière bien compliquée !) la parité de ![]() qui a été établie au tout début du présent article.
qui a été établie au tout début du présent article.
En effet, si ![]() est impair, alors tous les termes de la somme sont pairs et donc
est impair, alors tous les termes de la somme sont pairs et donc ![]() aussi. Et si
aussi. Et si ![]() est pair, alors tous les termes sont pairs sauf peut-être celui d’indice
est pair, alors tous les termes sont pairs sauf peut-être celui d’indice ![]() par conséquent,
par conséquent, ![]() est de la même parité que
est de la même parité que ![]() En posant
En posant ![]() avec
avec ![]() impair, une récurrence immédiate montre que
impair, une récurrence immédiate montre que![]() est de la même parité que
est de la même parité que ![]() donc est pair.
donc est pair.
4 – Fonction génératrice de la suite des coefficients binomiaux centraux
![Rendered by QuickLaTeX.com \[\left(1+x\right)^{\alpha}=\sum_{n=0}^{\infty}\binom{\alpha}{n}x^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0393d4019269e986dfec201c951cf7ab_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\frac{1}{\sqrt{1-4x}}=\sum_{n=0}^{\infty}\binom{-1/2}{n}\left(-4x\right)^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-32e1d1154713418644cf6c68ee75d1e4_l3.png)
![Rendered by QuickLaTeX.com \[\binom{-1/2}{n}=\frac{1}{n!}\prod_{k=0}^{n-1}\left(-\frac{1}{2}-k\right)=\frac{\left(-1\right)^{n}}{2^{n}\thinspace n!}\prod_{k=0}^{n-1}\left(2k+1\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e6754baacf1966e4de08df2df722bb92_l3.png)
![Rendered by QuickLaTeX.com \[\prod_{k=0}^{n-1}\left(2k+1\right)=\frac{\left(2n\right)!}{2\times4\times\cdots\times\left(2n\right)}=\frac{\left(2n\right)!}{2^{n}n!}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a3ea5bb5562df6aa015ea96bed52e96e_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\frac{1}{\sqrt{1-4x}}=\sum_{n=0}^{\infty}\binom{2n}{n}x^{n}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5fbe769501d18c3e9632d2b89866afa6_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\sum_{n=0}^{\infty}\frac{1}{8^{n}}\binom{2n}{n}=\sqrt{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-925a97d6cbb3f819f527fa147648541c_l3.png)
5 – Une formule remarquable pour 
Dans sa tentative de résolution du problème de Bâle, le mathématicien écossais James Stirling découvrit une formule inédite pour le nombre :
![Rendered by QuickLaTeX.com \[\sum_{n=1}^{\infty}\frac{1}{n^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c55ed410049f491d277526295f0d9f3e_l3.png)
![Rendered by QuickLaTeX.com \[\zeta\left(2\right)=\sum_{n=1}^{\infty}\frac{3}{n^{2}\binom{2n}{n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-616d7ba2e3cc29d6440c9843aaab9e99_l3.png)
Cependant, Stirling ne parvint pas à reconnaître qu’il s’agissait de ![]() … ce que fit par la suite Euler. A ce sujet, on pourra consulter cette vidéo :
… ce que fit par la suite Euler. A ce sujet, on pourra consulter cette vidéo :
Donnons une preuve détaillée de la formule :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\frac{\pi^2}{6}=\sum_{n=1}^{\infty}\frac{3}{n^{2}\binom{2n}{n}}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-33612e55c26d74bea2c3be0d1fd80f1b_l3.png)
Admettons temporairement que pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\frac{\arcsin\left(x\right)}{\sqrt{1-x^{2}}}=\sum_{n=1}^{\infty}W_{2n-1}x^{2n-1}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fc1c4d6555083715131dd58027a17382_l3.png)
![]()
Cette propriété sera établie à l’annexe 2.
Etant donné que :
![]()
![Rendered by QuickLaTeX.com \[\arcsin^{2}\left(x\right)=\sum_{n=1}^{\infty}\frac{W_{2n-1}}{n}x^{2n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ec1913b76bf2f5cbc85d0a8db8ba4b92_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[\arcsin^{2}\left(x\right)=\sum_{n=1}^{\infty}\frac{\left(2x\right)^{2n}}{2n^{2}\binom{2n}{n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-af6ca3a212d46eff14b94d4289fea168_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\forall x\in\left]-2,2\right[,\thinspace2\arcsin^{2}\left(\frac{x}{2}\right)=\sum_{n=1}^{\infty}\frac{x^{2n}}{n^{2}\binom{2n}{n}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-09bee163598f56f95037aa987b394030_l3.png)
![Rendered by QuickLaTeX.com \[\frac{\pi^{2}}{18}=\sum_{n=1}^{\infty}\frac{1}{n^{2}\binom{2n}{n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f0f42158c48a347817b205f5083b31df_l3.png)
En termes d’accélération de la convergence, le gain est spectaculaire ! Si l’on note :
![Rendered by QuickLaTeX.com \[A_{n}=\sum_{k=1}^{n}\frac{1}{k^{2}}\qquad\text{et}\qquad B_{n}=\sum_{k=1}^{n}\frac{3}{k^2\binom{2k}{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a4d6c907a1faa08ccb017b70f0177589_l3.png)
![]()
![]()
Annexe 1 – Preuve de la 2ème version de la formule de Legendre
Nous démontrons ici la :
Proposition
Pour tout entier ![]() et tout nombre premier
et tout nombre premier ![]() :
:
![]()
Commençons par exprimer ![]() en base
en base ![]() :
:
![Rendered by QuickLaTeX.com \[n=\sum_{k=0}^{d}\,a_{k}p^{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3ed1664ff588d247b862621a0cc5cf9b_l3.png)
On observe que pour tout ![]() :
:
(![]() )
) ![Rendered by QuickLaTeX.com \[\left\lfloor \frac{n}{p^{i}}\right\rfloor =\left\lfloor \sum_{k=i}^{d}\,a_{k}p^{k-i}+\sum_{k=0}^{i-1}\,a_{k}p^{k-i}\right\rfloor =\sum_{k=i}^{d}\,a_{k}p^{k-i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ebcec3c0c301f0bb91ddd8bf61249a93_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=i}^{d}\,a_{k}p^{k-i}\in\mathbb{N}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4f021054929ee4d2b0b1d321eca8e3b7_l3.png)
![Rendered by QuickLaTeX.com \[0\leqslant\sum_{k=0}^{i-1}\,a_{k}p^{k-i}\leqslant\left(p-1\right)\sum_{k=0}^{i-1}p^{k-i}<\left(p-1\right)\sum_{j=1}^{\infty}\frac{1}{p^{j}}=1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0c80fdcd8e4c1b5106ef500299843861_l3.png)
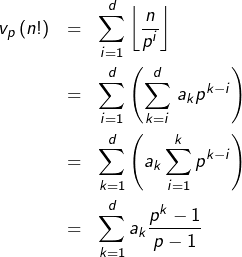
![Rendered by QuickLaTeX.com \[S_{p}\left(n\right)=\sum_{k=0}^{d}\,a_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0007d44ffe11944ce688577bde6908eb_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{v_{p}\left(n!\right)=\frac{n-S_{p}\left(n\right)}{p-1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-688ba05256b7909b940ea6c18f3e66ef_l3.png)
Annexe 2 – Un développement en série entière peu classique
Lemme
Pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\frac{\arcsin\left(x\right)}{\sqrt{1-x^{2}}}=\sum_{n=0}^{\infty}W_{2n+1}x^{2n+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5ca75e989b48d1e387f86943b65cb5fc_l3.png)
Partons de la série en utilisant la définition des intégrales de Wallis.
Pour tout ![]() :
:
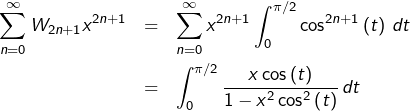
En remplaçant ![]() par
par ![]() au dénominateur puis en posant
au dénominateur puis en posant ![]() il vient :
il vient :
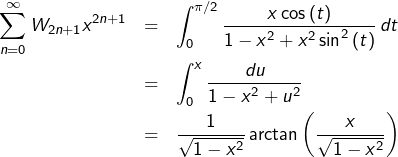
![]()
![Rendered by QuickLaTeX.com \[\boxed{\forall x\in\left]-1,1\right[,\thinspace\sum_{n=0}^{\infty}W_{2n+1}x^{2n+1}=\frac{\arcsin\left(x\right)}{\sqrt{1-x^{2}}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5c7fac1828f2c7059b27a29180caef0c_l3.png)
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.



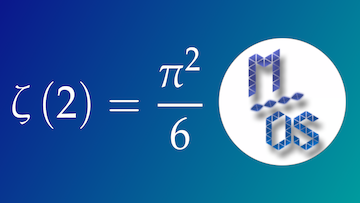
Bonjour,
Merci pour cet article instructif, notamment les deux formules de Legendre (ou plutôt la formule de Legendre et son autre formulation équivalente de l’annexe 1).
Concernant les 4 formules de la partie 3, il me semble que la première a des applications en Dénombrement / Probabilité. En revanche, je ne connais pas d’application des formules 2-3-4 (bien que leur esthétique suffise, une application n’étant pas du tout nécessaire !).
Bien à vous.