Il est facile de voir que l’ensemble ![]() des permutations de
des permutations de ![]() est infini. En effet, l’application
est infini. En effet, l’application ![]() définie par :
définie par :
![]()
![]()
![]()
![]()
est involutive, donc bijective. Et il existe clairement une infinité de telles « transpositions » …
La question que vous devrez résoudre est la suivante : ![]() est-il dénombrable ?
est-il dénombrable ?
Une solution est disponible ici


J’ai deux questions 🙂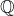 l’ensemble
l’ensemble 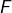 des suites binaires comportant un nombre fini de 1 ? De mon côté, je vois les choses ainsi : si l’on note
des suites binaires comportant un nombre fini de 1 ? De mon côté, je vois les choses ainsi : si l’on note 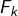 la partie de
la partie de 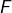 formée des suites
formée des suites 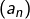 telles que
telles que 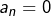 pour tout
pour tout 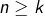 , alors il est clair que
, alors il est clair que 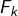 est fini pour tout
est fini pour tout 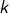 (plus précisément : son cardinal vaut
(plus précisément : son cardinal vaut 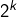 ) et que
) et que 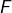 est l’union des
est l’union des 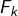 pour
pour 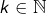 . Ainsi,
. Ainsi, 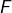 est l’union d’une famille dénombrable d’ensembles finis.
est l’union d’une famille dénombrable d’ensembles finis.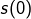 dans le cas où
dans le cas où 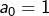 ?
?
1 – Pourriez-vous détailler comment vous injectez dans
2 – J’ai peut-être mal compris mais comment définissez-vous
1- On peut associer à la suite (ai) composée de 0 et de 1, le rationnel x : x= somme de i variant 0 à l’infini : ai*10^(-i)
Tout à fait d’accord avec votre point de vue.
2- Je me rends compte que je me suis très mal exprimé, je corrige :
Dans le cas où ai=1, on regarde non pas la parité des indices i mais la parité du nombre d’indices j inférieur ou égal à i tel que aj=1.
Voici un exemple pour lever toute ambiguïté, si les 10 premiers chiffres (on compte de 0 à 9) sont : 0100010011, cela signifie que les entiers 0,2,3,4,6,7 sont des points fixes de ma permutation, que 1 et 5 sont permutés, et 8 et 9 sont permutés.
C’est effectivement beaucoup plus clair. Et c’est en outre une manière élégante d’établir la non dénombrabilité de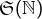 . Je vais très prochainement poster la solution que j’ai élaborée de mon côté, tout en indiquant la vôtre. Peut-être que d’autres points de vue apparaîtront par la suite … qui sait ? Internautes, à vos plumes !
. Je vais très prochainement poster la solution que j’ai élaborée de mon côté, tout en indiquant la vôtre. Peut-être que d’autres points de vue apparaîtront par la suite … qui sait ? Internautes, à vos plumes !
Prouvons que S(N) n’est pas dénombrable.
Considérons E l’ensemble des suites de 0 et de 1 qui contiennent une infinité de 1.
Cet ensemble n’est pas dénombrable car l’ensemble des suites de 0 et de 1 n’est pas dénombrable (équipotent à R) et l’ensemble des suites de 0 et 1 avec un nombre fini de 1 est dénombrable (cet ensemble s’injecte dans Q).
On va construire une injection de notre ensemble E dans S(N), ce qui suffit donc à prouver le résultat.
Soit une suite (ai) dans E, on lui associe la permutation s suivante :
Pour tout entier naturel i :
-si ai=0 alors s(i)=i,
-si ai=1, alors deux cas se produisent, si i est impair alors s(i)=j avec j le prochain indice j tel que aj=1, si i est pair, s(i)=j avec j le précédent indice j tel que aj=1.
Cette construction est possible par définition de E.