
Une question classique, située à la jonction entre théorie des groupes et topologie de ![]() consiste à décrire les sous-groupes additifs de
consiste à décrire les sous-groupes additifs de ![]() (SGA, en abrégé).
(SGA, en abrégé).
Rappelons qu’un SGA est une partie de ![]() contenant
contenant ![]() et stable par différence.
et stable par différence.
A cet égard, le principal résultat est le suivant :
Théorème
Etant donné un SGA ![]() de
de ![]() non réduit à
non réduit à ![]() et en notant
et en notant ![]() la borne inférieure de l’ensemble de ses éléments strictement positifs, de deux choses l’une :
la borne inférieure de l’ensemble de ses éléments strictement positifs, de deux choses l’une :
- ou bien
 auquel cas
auquel cas 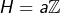
- ou bien
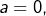 auquel cas
auquel cas 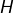 est une partie dense de
est une partie dense de 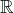
Vous pourrez en suivre une preuve détaillée dans cette vidéo :
Comme exemples de SGA, on peut citer :
- les parties de la forme
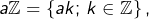 pour
pour 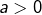 ,
, - les sommes de telles parties, comme
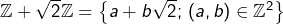 ,
, - l’ensemble
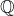 des nombres rationnels.
des nombres rationnels.
Voici maintenant une question qui n’est pas immédiate :
Existe-t-il des SGA qui soient non dénombrables ?
Évidemment, on met de côté la réponse évidente consistant à prendre ![]() lui-même.
lui-même.
L’objet de cet article est d’en proposer un exemple explicite. On s’intéresse à :
![]()
Il est facile de voir que ![]() est un SGA :
est un SGA :
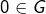 d’évidence
d’évidence- Si
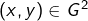 alors pour tout
alors pour tout 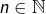 :
:
donc :![Rendered by QuickLaTeX.com \[\sin\left(\pi10^{10^{n}}\left(x-y\right)\right)=\sin\left(\pi10^{10^{n}}x\right)\cos\left(\pi10^{10^{n}}y\right)-\cos\left(\pi10^{10^{n}}x\right)\sin\left(\pi10^{10^{n}}y\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7ba405c830285a25c6fb2d282dd9edf0_l3.png)
et donc![Rendered by QuickLaTeX.com \[\left|\sin\left(\pi10^{10^{n}}\left(x-y\right)\right)\right|\leqslant\left|\sin\left(\pi10^{10^{n}}x\right)\right|+\left|\sin\left(\pi10^{10^{n}}y\right)\right|\underset{n\rightarrow\infty}{\rightarrow}0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fc552bbb2938b9dde0c6233e494a4c6a_l3.png)
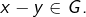
En outre, pour tout ![]()
![]() d’où l’existence d’un entier
d’où l’existence d’un entier ![]() tel que
tel que ![]() On voit alors que :
On voit alors que :
![]()
![]()
![Rendered by QuickLaTeX.com \[\varphi:\left\{ 0,1\right\} ^{\mathbb{N}}\rightarrow\mathbb{R},\thinspace u\mapsto\sum_{n=0}^{\infty}\frac{u_{n}}{10^{10^{n}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2eb34ecfbcfa08d42b8b0ed63c487727_l3.png)
![]()
La conclusion va maintenant résulter de l’inclusion ![]()
Soit ![]() Il existe une suite
Il existe une suite ![]() telle que :
telle que :
![Rendered by QuickLaTeX.com \[x=\sum_{k=0}^{\infty}\frac{u_{k}}{10^{10^{k}}}=S_{n}+R_{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1d6784679a564621e315b1a37f13e7ef_l3.png)
![Rendered by QuickLaTeX.com \[S_{n}=\sum_{k=0}^{n}\frac{u_{k}}{10^{10^{k}}}\qquad\text{et}\qquad R_{n}=\sum_{k=n+1}^{\infty}\frac{u_{k}}{10^{10^{k}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ba903d0e09721838e60af5422dfbb8e8_l3.png)
![]()
![]()
![]()
![]()
En conclusion, l’ensemble
![]()
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.


Bonjour Monsieur,
Merci pour cette vidéo et cet article très ludiques et instructifs.
Je dois être passé à côté d’une subtilité, mais pourquoi ne pas prendre simplement 10^n au lieu de 10^(10^n)) dans l’argument de la fonction sinus ?
Bien à vous.
Il me semble qu’avec 10^n, on n’a plus sin(pi 10^n Rn) qui tend vers 0 .