Une preuve de l'irrationalité de π

Dans cette vidéo, on établit l’irrationalité des nombres $e$ et $\pi$ , puis on explique pour quelle raison l’un au moins des deux nombres $e+\pi$ et $e\pi$ est nécessairement irrationnel. Toutefois, la preuve de l’irrationalité de $\pi$ est simplement esquissée dans la vidéo et le présent article en donne une version détaillée.

La preuve proposée est inspirée de celle produite par le mathématicien canadien Ivan Niven et publiée dans le Bulletin of the American Mathematical Society (numéro 53, en 1947) et que l’on peut lire ici.

Voici le plan adopté.

On note, pour tout $n\in\mathbb{N}$ :

$I_{n}=\frac{1}{n!}\int_{0}^{\pi}x^{n}\left(\pi-x\right)^{n}\sin\left(x\right)\thinspace dx$

et l’on prouve successivement que :

➡ $\forall n\in\mathbb{N},\thinspace I_{n}>0$

➡ $\forall q\in\mathbb{N},\thinspace{\displaystyle \lim_{n\rightarrow\infty}q^{n}I_{n}=0}$

➡ $\forall n\geqslant2,\thinspace I_{n}=\left(4n-2\right)I_{n-1}-\pi^{2}I_{n-2}$

➡ $\forall n\in\mathbb{N},\exists\left(c_{n,k}\right)_{0\leqslant k\leqslant n}\in\mathbb{Z}^{n+1};\thinspace{\displaystyle I_{n}=\sum_{k=0}^{n}c_{n,k}\pi^{k}}$

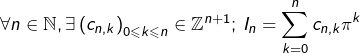
On raisonne alors par l’absurde. S’il existe $\left(p,q\right)\in\mathbb{N}^{\star2}$ tel que ${\displaystyle \pi=\frac{p}{q}},$ alors on déduit des points précédents que, pour $n$ assez grand, le nombre $q^{n}I_{n}$ est un entier strictement compris entre 0 et 1, ce qui apporte la contradiction souhaitée.

Voyons maintenant tout cela en détail.

Preuve des deux premiers points

Il est clair que, pour tout $n\in\mathbb{N},$ l’application $f_{n}:\left[0,\pi\right]\rightarrow\mathbb{R},\thinspace x\mapsto x^{n}\left(\pi-x\right)^{n}\sin\left(x\right)$ est continue et positive. Elle est en outre non identiquement nulle, puisque :

$f_{n}\left(\frac{\pi}{2}\right)=\left(\frac{\pi}{2}\right)^{2n}>0$

Son intégrale est donc strictement positive et donc $I_{n}>0.$

Par ailleurs, pour tout $\left(n,x\right)\in\mathbb{N}\times\left[0,\pi\right]$ :

$x^{n}\left(\pi-x\right)^{n}\sin\left(x\right)\leqslant\pi^{2n}$

donc, quel que soit l’entier $q\in\mathbb{N}^\star$ :

$0<q^{n}I_{n}\leqslant\frac{q^{n}}{n!}\pi\left(\pi^{2}\right)^{n}=\pi\frac{\left(q\pi^{2}\right)^{n}}{n!}$

Pour conclure que $\lim_{n\rightarrow\infty}q^{n}I_{n}=0$ , il suffit alors d’invoquer le :

Lemme

Pour tout réel $a>0$ :

$\lim_{n\rightarrow\infty}\frac{a^{n}}{n!}=0$

Preuve (cliquer pour déplier / replier)

Si l’on note $\displaystyle{u_{n}=\frac{a^{n}}{n!}}$ , alors pour tout $n\in\mathbb{N}$ :

$\frac{u_{n+1}}{u_{n}}=\frac{a^{n+1}}{\left(n+1\right)!}\thinspace\frac{n!}{a^{n}}=\frac{a}{n+1}$

et donc $\lim_{n\rightarrow\infty}\frac{u_{n+1}}{u_{n}}=0.$

En particulier :

$\frac{u_{n+1}}{u_{n}}<1\text{ dès que }n\text{ est assez grand}$

Autrement dit, la suite $u$ décroît APCR. Comme elle est minorée (par $0),$ elle converge. Notons $L$ sa limite. En passant à la limite dans l’égalité :

$u_{n+1}=\frac{a}{n+1}\thinspace u_{n}$

on voit que $L=0\times L,$ soit $L=0.$

Remarque

Si l’on connaît la règle de d’Alembert pour les séries à termes strictement positifs, on peut conclure plus rapidement.

En effet, comme $\lim_{n\rightarrow\infty}\frac{u_{n+1}}{u_{n}}=0$ , alors la série $\sum_{n\geqslant0}u_{n}$ converge et, en particulier, la suite $u$ converge vers $0.$

Preuve du troisième point

Nous allons utiliser la formule de double-intégration par parties (histoire d’accélérer un peu le calcul qui consisterait à détailler deux IPP successives).

D’une manière générale, si $f,g:\left[a,b\right]\rightarrow\mathbb{R}$ sont deux applications de classe $C^{2}$ alors :

$\fcolorbox{black}{myBlue}{$\int_{a}^{b}f\left(x\right)g''\left(x\right)\thinspace dx=\left[f\left(x\right)g'\left(x\right)-f'\left(x\right)g\left(x\right)\right]_{a}^{b}+\int_{a}^{b}f''\left(x\right)g\left(x\right)\thinspace dx$}$

Dans le cas qui nous intéresse, on choisit

$f(x)=\left(\pi x-x^{2}\right)^{n}\qquad\text{et}\qquad g(x)=-\sin(x)$

et l’on obtient pour tout $n\geqslant2$ :

$\begin{equation*}\begin{split}\int_{0}^{\pi}\left(\pi x-x^{2}\right)^{n}\sin\left(x\right)\thinspace dx & = \left[-\left(\pi x-x^{2}\right)^{n}\cos\left(x\right)+\right.\\& \qquad\left.n\left(\pi x-x^{2}\right)^{n-1}\left(\pi-2x\right)\sin\left(x\right)\right]_{x=0}^{\pi}\\& -\int_{0}^{\pi}\left(n\left(n-1\right)\left(\pi x-x^{2}\right)^{n-2}\left(\pi-2x\right)^{2}-\right.\\& \qquad\left.2n\left(\pi x-x^{2}\right)^{n-1}\right)\sin\left(x\right)\thinspace dx\end{split}\end{equation*}$

Le terme entre crochets est nul. De plus, on observe que :

$\left(\pi-2x\right)^{2}=\pi^{2}-4\pi x+4x^{2}=\pi^{2}-4\left(\pi x-x^{2}\right)$

Il vient donc :

$\int_{0}^{\pi}\left(\pi x-x^{2}\right)^{n}\sin\left(x\right)\thinspace dx = 2n\int_{0}^{\pi}\left(\pi x-x^{2}\right)^{n-1}\sin\left(x\right)\thinspace dx -K_n\qquad\left(\spadesuit\right)$

avec :

$\begin{equation*}\begin{split}K_n & = n\left(n-1\right)\int_{0}^{\pi}\left(\pi x-x^{2}\right)^{n-2}\left(\pi^{2}-4\left(\pi x-x^{2}\right)\right)\thinspace\sin\left(x\right)\thinspace dx\\ & = \pi^2n! I_{n-2}-4(n-1)\,n!I_{n-1}\end{split}\end{equation*}$

d’où, après division par $n!$ de chaque membre de $\left(\spadesuit\right)$ :

$I_{n}=2I_{n-1}-\left(\pi^{2}I_{n-2}-4(n-1)I_{n-1}\right)$

soit finalement :

$\fcolorbox{black}{myBlue}{$I_{n}=\left(4n-2\right)I_{n-1}-\pi^{2}I_{n-2}$}$

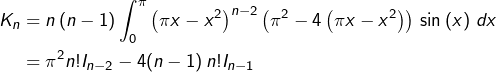
Preuve du quatrième point

La formule annoncée s’obtient en raisonnant par récurrence. On calcule aisément :

$I_{0}=\int_{0}^{\pi}\sin\left(x\right)\thinspace dx$

c’est-à-dire :

$\fcolorbox{black}{myBlue}{$I_{0}=2$}$

puis :

$I_{1}=\int_{0}^{\pi}\left(\pi x-x^{2}\right)\sin\left(x\right)\thinspace dx$

donc (double IPP) :

$I_{1}=\left[-\left(\pi x-x^{2}\right)\cos\left(x\right)+\left(\pi-2x\right)\sin\left(x\right)\right]_{0}^{\pi}+\int_{0}^{\pi}2\sin\left(x\right)\thinspace dx$

c’est-à-dire :

$\fcolorbox{black}{myBlue}{$I_{1}=4$}$

Il existe donc un polynôme $P_{0}\in\mathbb{Z}_{0}\left[X\right]$ et un polynôme $P_{1}\in\mathbb{Z}_{1}\left[X\right]$ tels que $I_{0}=P_{0}\left(\pi\right)$ et $I_{1}=P_{1}\left(\pi\right).$ Il s’agit d’évidence de $P_{0}=2$ et $P_{1}=4.$ Supposons, pour un certain $n\geqslant2,$ l’existence de polynômes $P_{n-2}\in\mathbb{Z}_{n-2}\left[X\right]$ et $P_{n-1}\in\mathbb{Z}_{n-1}\left[X\right]$ tels que :

$I_{n-2}=P_{n-2}\left(\pi\right)\quad\text{et}\quad I_{n-1}=P_{n-1}\left(\pi\right)$

alors, d’après la formule établie au troisième point :

$I_{n}=\left(4n-2\right)P_{n-1}\left(\pi\right)-\pi^{2}P_{n-2}\left(\pi\right)$

et donc $I_{n}=P_{n}\left(\pi\right)$ où l’on a posé :

$P_{n}=\left(4n-2\right)P_{n-1}-X^{2}P_{n-2}$

Visiblement : $P_{n}\in\mathbb{Z}_{n}\left[X\right].$

On a prouvé par récurrence que, pour tout $n\in\mathbb{N},$ il existe $P_{n}\in\mathbb{Z}_{n}\left[X\right]$ vérifiant $I_{n}=P_{n}\left(\pi\right)$ .

De manière plus explicite, pour tout $n\in\mathbb{N},$ il existe des entiers $c_{n,0},\cdots,c_{n,n}$ tel que :

$I_{n}=\sum_{k=0}^{n}c_{n,k}\pi^{k}$

Preuve de l’irrationalité de π

Supposons $\pi$ rationnel et soient $p,q$ des entiers naturels non nuls tels que :

$\pi=\frac{p}{q}$

Alors, pour tout $n\in\mathbb{N}$ :

$q^{n}I_{n}=q^{n}\sum_{k=0}^{n}c_{n,k}\left(\frac{p}{q}\right)^{k}=\sum_{k=0}^{n}c_{n,k}p^{k}q^{n-k}$

Il en résulte que $q^{n}I_{n}\in\mathbb{Z}.$ Mais on vu au premier point que $q^{n}I_{n}>0$ et donc $q^{n}I_{n}\in\mathbb{N}^{\star}.$

Par ailleurs, comme $\lim_{n\rightarrow\infty}q^{n}I_{n}=0$ (second point) alors $q^{n}I_{n}<1$ dès que $n\geqslant n_{0}$ convenable.

Nous sommes parvenus à la contradiction désirée : si $n$ est assez grand, $q^{n}I_{n}$ est un entier strictement compris entre 0 et 1.

Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Partager cet article