Deux formules de moyenne pour les intégrales

Il existe deux formules de moyenne pour les intégrales.

Elles sont attribuées au mathématicien Pierre-Ossian Bonnet (1819 – 1892).

On se propose de les énoncer, de les établir et d’en donner des exemples significatifs d’utilisation.

Des versions plus fortes de ces résultats existent dans la littérature, mais on a choisi ici de privilégier la simplicité à la généralité.

Première formule de la moyenne

On suppose que $\varphi$ et $\psi$ sont des applications continues d’un segment $\left[a,b\right]$ dans $\mathbb{R}.$

Proposition 1

Si $\psi$ est positive, alors il existe $c\in\left[a,b\right]$ tel que :

$\int_{a}^{b}\varphi\left(t\right)\psi\left(t\right)\thinspace dt=\varphi\left(c\right)\int_{a}^{b}\psi\left(t\right)\thinspace dt$

Notons respectivement $m$ et $M$ le minimum et le maximum de $\varphi.$ Pour tout $t\in\left[a,b\right]$ :

$m\leqslant\varphi\left(t\right)\leqslant M$

donc, comme $\psi$ est positive :

$m\thinspace\psi\left(t\right)\leqslant\varphi\left(t\right)\thinspace\psi\left(t\right)\leqslant M\thinspace\psi\left(t\right)$

puis, par croissance de l’intégrale :

$m\thinspace\int_{a}^{b}\thinspace\psi\left(t\right)\thinspace dt\leqslant\int_{a}^{b}\varphi\left(t\right)\psi\left(t\right)\thinspace dt\leqslant M\thinspace\int_{a}^{b}\thinspace\psi\left(t\right)\thinspace dt$

Supposons $\psi$ non identiquement nulle, ce qui entraîne $\int_{a}^{b}\thinspace\psi\left(t\right)\thinspace dt>0$ , car $\psi$ est continue et positive. Alors :

$m\leqslant\dfrac{\int_{a}^{b}\varphi\left(t\right)\psi\left(t\right)\thinspace dt}{\int_{a}^{b}\psi\left(t\right)\thinspace dt}\leqslant M$

et le TVI garantit l’existence d’un réel $c\in\left[a,b\right]$ tel que :

$\dfrac{\int_{a}^{b}\varphi\left(t\right)\psi\left(t\right)\thinspace dt}{\int_{a}^{b}\psi\left(t\right)\thinspace dt}=\varphi\left(c\right)$

ce qui donne la conclusion. Et cette conclusion est évidente dans le cas où $\psi$ est l’application nulle !

Remarque 1

On peut remplacer l’hypothèse $\psi$ positive par $\psi$ de signe constant. Si $\psi$ est à valeurs négatives, il suffit en effet d’appliquer ce qui précède au couple $\left(\varphi,-\psi\right).$

En outre, la continuité de $\psi$ n’a pas servi : on peut se contenter de supposer que $\psi$ est continue par morceaux, ou même seulement Riemann-intégrable.

Remarque 2

En choisissant pour $\psi$ la fonction constante égale à 1, on obtient pour toute application continue $\varphi:\left[a,b\right]\rightarrow\mathbb{R}$ , l’existence d’un réel $c\in\left[a,b\right]$ tel que :

$\dfrac{1}{b-a}\int_{a}^{b}\varphi\left(t\right)\thinspace dt=\varphi\left(c\right)$

Le membre de gauche de cette égalité est appelé la valeur moyenne de $\varphi$ (voir la fin de cette note).

Seconde formule de la moyenne

On suppose toujours que $\varphi$ et $\psi$ sont des applications d’un segment $\left[a,b\right]$ dans $\mathbb{R}.$

Proposition 2

Si $\varphi$ est décroissante et positive et si $\psi$ est continue par morceaux (ou seulement Riemann-intégrable), alors il existe $c\in\left[a,b\right]$ tel que :

$\int_{a}^{b}\varphi\left(t\right)\psi\left(t\right)\thinspace dt=\varphi\left(a\right)\int_{a}^{c}\psi\left(t\right)\thinspace dt$

Preuve simplifiée n° 1

➡ Supposons en outre $\psi\geqslant0.$

L’application :

$J:\left[a,b\right]\rightarrow\mathbb{R},\thinspace x\mapsto\varphi\left(a\right)\int_{a}^{x}\psi\left(t\right)\thinspace dt$

est continue et de plus :

$J\left(a\right)=0\leqslant\int_{a}^{b}\varphi\left(t\right)\psi\left(t\right)\thinspace dt\leqslant\varphi\left(a\right)\int_{a}^{b}\psi\left(t\right)\thinspace dt=J\left(b\right)$

donc (TVI) :

$\exists c\in\left[a,b\right];\thinspace \int_{a}^{b}\varphi\left(t\right)\thinspace\psi\left(t\right)=J\left(c\right)$

Remarque

Sans hypothèse de positivité pour $\varphi,$ on peut considérer plutôt :

$K:\left[a,b\right]\rightarrow\mathbb{R},\thinspace x\mapsto\varphi\left(a\right)\int_{a}^{x}\psi\left(t\right)\thinspace dt+\varphi\left(b\right)\int_{x}^{b}\psi\left(t\right)\thinspace dt$

et observer (grâce à la décroissance de $\varphi$ et à la positivité de $\psi)$ que :

$K\left(a\right)=\varphi\left(b\right)\int_{a}^{b}\psi\left(t\right)\thinspace dt\leqslant\int_{a}^{b}\varphi\left(t\right)\psi\left(t\right)\thinspace dt\leqslant\varphi\left(a\right)\int_{a}^{b}\psi\left(t\right)\thinspace dt=K\left(b\right)$

Le TVI appliqué à $K$ (qui est continue !) montre alors qu’il existe $c\in\left[a,b\right]$ tel que $\int_{a}^{b}\varphi\left(t\right)\psi\left(t\right)\thinspace dt=K\left(c\right);$ c’est-à-dire :

$\fcolorbox{black}{myBlue}{$\displaystyle{\int_{a}^{b}\varphi\left(t\right)\psi\left(t\right)\thinspace dt=\varphi\left(a\right)\int_{a}^{c}\psi\left(t\right)\thinspace dt+\varphi\left(b\right)\int_{c}^{b}\psi\left(t\right)\thinspace dt}$}$

Preuve simplifiée n° 2

➡ Supposons en outre $\varphi$ de classe $C^{1}$ et $\psi$ continue.

Posons $\Psi\left(x\right)=\int_{a}^{x}\,\psi\left(t\right)\,dt.$ Comme $\psi$ est continue, $\Psi$ est de classe $C^{1}$ et $\Psi'=\psi.$ Après intégration par parties :

$\int_{a}^{b}\,\varphi\left(t\right)\,\psi\left(t\right)\,dt=\int_{a}^{b}\,\varphi\left(t\right)\,\Psi'\left(t\right)\,dt=\left[\varphi\left(t\right)\,\Psi\left(t\right)\right]_{a}^{b}-\int_{a}^{b}\,\varphi'\left(t\right)\,\Psi\left(t\right)\,dt$

Comme $\varphi'$ est de signe constant, la première formule de la moyenne s’applique. Il existe $\alpha\in\left[a,b\right]$ tel que :

$\int_{a}^{b}\,\varphi'\left(t\right)\,\Psi\left(t\right)\,dt=\Psi\left(\alpha\right)\,\int_{a}^{b}\,\varphi'\left(t\right)dt=\Psi\left(\alpha\right)\left(\varphi\left(b\right)-\varphi\left(a\right)\right)$

et donc :

$\int_{a}^{b}\,\varphi\left(t\right)\,\psi\left(t\right)\,dt=\varphi\left(b\right)\,\Psi\left(b\right)+\left(\varphi\left(a\right)-\varphi\left(b\right)\right)\,\Psi\left(\alpha\right)$

Si $\varphi\left(a\right)=0,$ comme $\varphi$ est décroissante et positive, alors $\varphi=0$ et la formule à établir est évidente.

Sinon :

$\int_{a}^{b}\,\varphi\left(t\right)\,\psi\left(t\right)\,dt=\varphi\left(a\right)\,\left[\frac{\varphi\left(b\right)}{\varphi\left(a\right)}\,\Psi\left(b\right)+\left(1-\frac{\varphi\left(b\right)}{\varphi\left(a\right)}\right)\,\Psi\left(\alpha\right)\right]$

Comme $\dfrac{\varphi\left(b\right)}{\varphi\left(a\right)}\in\left[0,1\right],$ la quantité entre crochets est comprise entre $\Psi\left(b\right)$ et $\Psi\left(\alpha\right).$ D’après le TVI, il existe donc $c\in\left[a,b\right]$ tel que :

$\int_{a}^{b}\,\varphi\left(t\right)\,\psi\left(t\right)\,dt=\varphi\left(a\right)\,\Psi\left(c\right)$

comme souhaité.

Preuve simplifiée n° 3

➡ Supposons en outre $\varphi$ continue.

Etant donné $n\in\mathbb{N}^{\star},$ notons pour tout $j\in\left\llbracket 0,n-1\right\rrbracket$ :

$t_{j}=a+\dfrac{j\left(b-a\right)}{n}$

Les nombres $t_{j}$ , qui forment une subdivision régulière du segment $\left[a,b\right]$ , devraient d’ailleurs être notés $t_{n,j}$ , car ils dépendent aussi de $n$ … mais on ne va pas alourdir les notations. Posons aussi :

$S_{n}=\sum_{j=0}^{n-1}\int_{t_{j}}^{t_{j+1}}\thinspace\varphi\left(t_{j}\right)\psi\left(t\right)\thinspace dt$

et montrons que :

( $\star$ ) $\fcolorbox{black}{myBlue}{$\displaystyle{\lim_{n\rightarrow+\infty}S_{n}=\int_{a}^{b}\varphi\left(t\right)\psi\left(t\right)\thinspace dt}$}$

Pour tout $n\in\mathbb{N}^{\star}$ :

$S_{n}-\int_{a}^{b}\varphi\left(t\right)\psi\left(t\right)\thinspace dt=\sum_{j=0}^{n-1}\int_{t_{j}}^{t_{j+1}}\left(\varphi\left(t_{j}\right)-\varphi\left(t\right)\right)\thinspace\psi\left(t\right)\thinspace dt$

donc :

$\left|S_{n}-\int_{a}^{b}\varphi\left(t\right)\psi\left(t\right)\thinspace dt\right|\leqslant\sum_{j=0}^{n-1}\int_{t_{j}}^{t_{j+1}}\left|\varphi\left(t_{j}\right)-\varphi\left(t\right)\right|\thinspace\left|\psi\left(t\right)\right|\thinspace dt$

Comme $\varphi$ est uniformément continue (d’après le théorème de Heine), étant donné $\epsilon>0$ il existe $\delta>0$ tel que :

$\forall\left(s,t\right)\in\left[a,b\right]^{2},\thinspace\left|s-t\right|\leqslant\delta\Rightarrow\left|\varphi\left(s\right)-\varphi\left(t\right)\right|\leqslant\epsilon$

Ainsi, dès que $n\geqslant\dfrac{b-a}{\delta}$ :

$\forall j\in\left\llbracket 0,n-1\right\rrbracket ,\thinspace\forall t\in\left[t_{j},t_{j+1}\right],\thinspace\left|\varphi\left(t_{j}\right)-\varphi\left(t\right)\right|\leqslant\epsilon$

donc :

$\left|S_{n}-\int_{a}^{b}\varphi\left(t\right)\psi\left(t\right)\thinspace dt\right|\leqslant\epsilon\int_{a}^{b}\left|\psi\left(t\right)\right|\thinspace dt$

et la relation $\left(\star\right)$ est établie.

Par ailleurs, en notant

$\Psi:[a,b]\to\mathbb{R},\,x\mapsto\int_{a}^{x}\psi\left(t\right)\thinspace dt$

une transformation d’Abel donne :

$\begin{eqnarray*}S_{n} & = & \sum_{j=0}^{n-1}\varphi\left(t_{j}\right)\left(\Psi\left(t_{j+1}\right)-\Psi\left(t_{j}\right)\right)\\& = & \varphi\left(t_{n-1}\right)\Psi\left(t_{n}\right)+\sum_{j=1}^{n-1}\left(\varphi\left(t_{j-1}\right)-\varphi\left(t_{j}\right)\right)\Psi\left(t_{j}\right)\end{eqnarray*}$

Notons $m$ et $M$ le minimum et le maximum de $\Psi.$ Vu que $\varphi$ est positive :

$\varphi\left(t_{n-1}\right)\thinspace m\leqslant\varphi\left(t_{n-1}\right)\Psi\left(t_{n}\right)\leqslant\varphi\left(t_{n-1}\right)\thinspace M$

et vu que $\varphi$ est décroissante, on a pour tout $j\in\left\llbracket 0,n-1\right\rrbracket$ :

$\left(\varphi\left(t_{j-1}\right)-\varphi\left(t_{j}\right)\right)m\leqslant\left(\varphi\left(t_{j-1}\right)-\varphi\left(t_{j}\right)\right)\Psi\left(t_{j}\right)\leqslant\left(\varphi\left(t_{j-1}\right)-\varphi\left(t_{j}\right)\right)M$

donc (sommation télescopique) :

$m\thinspace\varphi\left(a\right)\leqslant S_{n}\leqslant M\thinspace\varphi\left(a\right)$

En passant à la limite et d’après $(\star)$ :

$m\thinspace\varphi\left(a\right)\leqslant\int_{a}^{b}\varphi\left(t\right)\thinspace\psi\left(t\right)\thinspace dt\leqslant M\thinspace\varphi\left(a\right)$

Si $\varphi\left(a\right)=0$ alors $\varphi=0$ et la formule à démontrer est évidente. Et sinon :

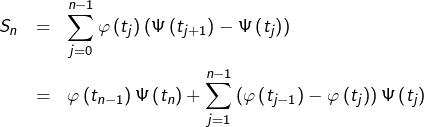
$m\leqslant\dfrac{\int_{a}^{b}\varphi\left(t\right)\thinspace\psi\left(t\right)\thinspace dt}{\varphi\left(a\right)}\leqslant M$

donc, d’après le TVI, il existe $c\in\left[a,b\right]$ tel que

$\dfrac{\int_{a}^{b}\varphi\left(t\right)\thinspace\psi\left(t\right)\thinspace dt}{\varphi\left(a\right)}=\Psi\left(c\right)$

ce qui donne la conclusion.

Preuve du cas général

Rappel : on suppose $\varphi$ décroissante positive et $\psi$ continue par morceaux (ou seulement Riemann-intégrable).

Nous allons constater que la relation $\left(\star\right)$ de la preuve simplifiée n° 3 reste vraie. En gros, on perd l’uniforme continuité de $\varphi$ mais on a toujours celle de

$\Psi^{\star}:\left[a,b\right]\rightarrow\mathbb{R},x\mapsto\int_{a}^{x}\left|\psi\left(t\right)\right|\thinspace dt$

Pour tout $n\geqslant1$ :

$\begin{eqnarray*}\left|S_{n}-\int_{a}^{b}\varphi\left(t\right)\psi\left(t\right)\thinspace dt\right| & \leqslant & \sum_{j=0}^{n-1}\int_{t_{j}}^{t_{j+1}}\left(\varphi\left(t_{j}\right)-\varphi\left(t\right)\right)\thinspace\left|\psi\left(t\right)\right|\thinspace dt\\& \leqslant & \sum_{j=0}^{n-1}\left(\varphi\left(t_{j}\right)-\varphi\left(t_{j+1}\right)\right)\int_{t_{j}}^{t_{j+1}}\left|\psi\left(t\right)\right|\thinspace dt\\& = & \sum_{j=0}^{n-1}\left(\varphi\left(t_{j}\right)-\varphi\left(t_{j+1}\right)\right)\left(\Psi^{\star}\left(t_{j+1}\right)-\Psi^{\star}\left(t_{j}\right)\right)\end{eqnarray*}$

Notons, pour tout $\delta\in\left]0,b-a\right[$ :

$\omega\left(\delta\right)=\sup_{a\leqslant t\leqslant b-\delta}\left(\Psi^{\star}\left(t+\delta\right)-\Psi^{\star}\left(t\right)\right)$

Comme $\Psi^{\star}$ est uniformément continue (d’après le théorème de Heine) : $\lim_{\delta\rightarrow0}\omega\left(\delta\right)=0.$ Or, d’après ce qui précède :

$\left|S_{n}-\int_{a}^{b}\varphi\left(t\right)\psi\left(t\right)\thinspace dt\right|\leqslant\omega\left(\dfrac{b-a}{n}\right)\thinspace\left(\varphi\left(a\right)-\varphi\left(b\right)\right)$

On retrouve ainsi $\left(\star\right)$ et l’on conclut ensuite comme à la preuve simplifiée n° 3.

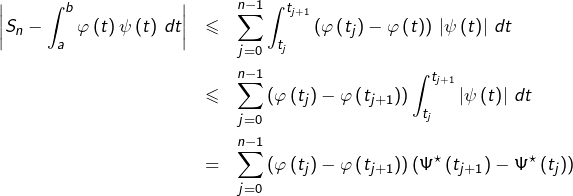
Deux exemples d’utilisation

➡ Exemple 1

Soit $T>0.$ On considère une application continue $f:\left[0,T\right]\rightarrow\mathbb{R}$ , une application $g:\mathbb{R}\rightarrow\mathbb{R}$ continue et $T-$ périodique et l’on s’intéresse au calcul de :

$\lim_{n\rightarrow+\infty}\int_{0}^{T}f\left(t\right)g\left(nt\right)\thinspace dt$

Pour tout $n\in\mathbb{N}^{\star},$ posons :

$J_{n}=\int_{0}^{T}f\left(t\right)g\left(nt\right)\thinspace dt$

Le changement de variable $x=nt$ donne :

$J_{n}=\dfrac{1}{n}\int_{0}^{nT}f\left(\dfrac{x}{n}\right)g\left(x\right)\thinspace dx$

puis, d’après la relation de Chasles :

$J_{n}=\dfrac{1}{n}\sum_{k=0}^{n-1}\int_{kT}^{\left(k+1\right)T}f\left(\dfrac{x}{n}\right)g\left(x\right)\thinspace dx$

Nouveau changement de variable … On pose $x=s+kT$ dans la $k-$ ème intégrale :

$J_{n}=\dfrac{1}{n}\sum_{k=0}^{n-1}\int_{0}^{T}f\left(\dfrac{s+kT}{n}\right)g\left(s+kT\right)\thinspace ds$

et comme $g$ est $T-$ périodique :

$J_{n}=\dfrac{1}{n}\sum_{k=0}^{n-1}\int_{0}^{T}f\left(\dfrac{s+kT}{n}\right)g\left(s\right)\thinspace ds$

A présent, on suppose $g$ de signe constant et on applique la première formule de la moyenne : pour chaque $k\in\left\llbracket 0,n-1\right\rrbracket ,$ il existe $c_{k}\in\left[0,T\right]$ tel que

$\int_{0}^{T}f\left(\dfrac{s+kT}{n}\right)g\left(s\right)\thinspace ds=f\left(\dfrac{c_{k}+kT}{n}\right)\thinspace\int_{0}^{T}g\left(s\right)\thinspace ds$

de sorte que :

$J_{n}=S_{n}\thinspace\int_{0}^{T}g\left(s\right)\thinspace ds\qquad\text{avec : }R_{n}=\dfrac{1}{n}\sum_{k=0}^{n-1}f\left(\dfrac{c_{k}+kT}{n}\right)$

On reconnaît que $R_{n}$ est une somme de Riemann attachée à $f$ sur $\left[0,T\right]$ et donc, d’après le théorème de convergence des sommes de Riemann :

$\lim_{n\rightarrow+\infty}J_{n}=\left(\int_{0}^{T}f\left(s\right)\thinspace ds\right)\left(\dfrac{1}{T}\int_{0}^{T}g\left(s\right)\thinspace ds\right)$

Si $g$ n’est pas de signe constant, on peut néanmoins trouver $\lambda\in\mathbb{R}$ tel que $\gamma:t\mapsto\lambda+g\left(t\right)$ soit de signe constant (il suffit de choisir $\lambda\geqslant-\inf_{\left[0,T\right]}g).$ On voit alors que :

$\begin{eqnarray*}J_{n} & = & \int_{0}^{T}f\left(t\right)\gamma\left(nt\right)\thinspace dt-\lambda\thinspace\int_{0}^{T}f\left(t\right)\thinspace dt\\& \underset{n\rightarrow+\infty}{\longrightarrow} & \left(\int_{0}^{T}f\left(s\right)\thinspace ds\right)\left(\dfrac{1}{T}\int_{0}^{T}\gamma\left(s\right)\thinspace ds\right)-\lambda\thinspace\int_{0}^{T}f\left(t\right)\thinspace dt\\& = & \left(\int_{0}^{T}f\left(s\right)\thinspace ds\right)\left(\dfrac{1}{T}\int_{0}^{T}g\left(s\right)\thinspace ds\right)\end{eqnarray*}$

Bref, il est maintenant établi que :

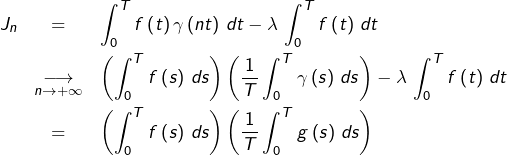
$\boxed{\lim_{n\rightarrow+\infty}\int_{0}^{T}f\left(t\right)g\left(nt\right)\thinspace dt=\left(\int_{0}^{T}f\left(s\right)\thinspace ds\right)\left(\dfrac{1}{T}\int_{0}^{T}g\left(s\right)\thinspace ds\right)}$

Remarque

Le lecteur pourra démontrer en exercice une formule un peu plus générale, à savoir que si $f$ est définie sur $\left[a,b\right]$ (au lieu de $\left[0,T\right]),$ on obtient en fin de compte :

$\fcolorbox{black}{myBlue}{$\displaystyle{\lim_{n\rightarrow+\infty}\int_{a}^{b}f\left(t\right)g\left(nt\right)\thinspace dt=\left(\int_{a}^{b}f\left(s\right)\thinspace ds\right)\left(\dfrac{1}{T}\int_{0}^{T}g\left(s\right)\thinspace ds\right)}$}$

ce qui constitue une jolie généralisation du lemme de Riemann-Lebesgue !

A titre d’exemple :

$\lim_{n\rightarrow\infty}\int_{0}^{1}\,\ln\left(1+t\right)\left|\sin\left(nt\right)\right|\,dt=\frac{2}{\pi}\left(2\ln\left(2\right)-1\right)$

En effet, l’application $t\mapsto\sin(nt)$ est $\pi-$ périodique de valeur moyenne égale à $\dfrac{2}{\pi}$ et par ailleurs :

$\int_0^1\ln(1+t)\,dt=\left[(t+1)\ln(1+t)\right]_0^1-\int_0^1dt=2\ln(2)-1$

➡ Exemple 2

Soit $f:\mathbb{R}^{+}\rightarrow\mathbb{R}$ continue telle que l’intégrale $\int_{0}^{+\infty}f\left(t\right)\thinspace dt$ soit semi-convergente. Pour tout $x\in\left[0,+\infty\right[,$ posons :

$F\left(x\right)=\int_{0}^{+\infty}\,e^{-xt}\,f\left(t\right)\,dt$

Montrons que $F$ est bien définie et continue.

$F\left(0\right)$ est bien défini par hypothèse. Et pour $x>0,$ l’intégrale $\int_{0}^{+\infty}e^{-xt}f\left(t\right)\thinspace dt$ existe d’après le critère de Cauchy. En effet, étant donné $\epsilon>0,$ il existe $A>0$ tel que pour tout $\left(a,b\right)\in\left[0,+\infty\right[^{2}$ :

$b>a\geqslant A\Rightarrow\left|\int_{a}^{b}f\left(t\right)\thinspace dt\right|\leqslant\epsilon$

Donc, d’après la seconde formule de la moyenne (le cas simplifié n° 2 suffit), dès que $b>a\geqslant A,$ il existe $c\in\left[a,b\right]$ tel que :

$\left|\int_{a}^{b}e^{-xt}f\left(t\right)\thinspace dt\right|=e^{-xa}\left|\int_{a}^{c}f\left(t\right)\thinspace dt\right|$

d’où :

$\left|\int_{a}^{b}e^{-xt}f\left(t\right)\thinspace dt\right|\leqslant\left|\int_{a}^{c}f\left(t\right)\thinspace dt\right|\leqslant\epsilon$

Désormais, posons pour tout $n\in\mathbb{N}$ et tout $x\in\left[0,+\infty\right[$ :

$F_{n}\left(x\right)=\int_{0}^{n}e^{-xt}f\left(t\right)\thinspace dt$

Comme $f$ est continue alors chaque $F_{n}$ aussi. Si l’on montre que la suite $\left(F_{n}\right)_{n\geqslant0}$ converge uniformément sur $\left[0,+\infty\right[$ vers $F,$ il en résultera que $F$ est continue. On utilise pour cela le critère de Cauchy uniforme. Pour tout $\left(p,q\right)\in\mathbb{N}^{2}$ tel que $q>p\geqslant A$ et pour tout $x\in\left[0,+\infty\right[$ :

$\left|F_{q}\left(x\right)-F_{p}\left(x\right)\right|=\left|\int_{p}^{q}e^{-xt}f\left(t\right)\thinspace dt\right|=e^{-xp}\left|\int_{p}^{c}f\left(t\right)\thinspace dt\right|$

où $c\in\left[p,q\right].$ Ainsi :

$\left|F_{q}\left(x\right)-F_{p}\left(x\right)\right|\leqslant\left|\int_{p}^{c}f\left(t\right)\thinspace dt\right|\leqslant\epsilon$

d’où le résultat annoncé.

Un cas particulier célèbre est celui où :

$f:\left[0,+\infty\right[\rightarrow\mathbb{R},\thinspace t\mapsto\left\{ \begin{array}{cc}\dfrac{\sin\left(t\right)}{t} & \text{si }t>0\\\\1 & \text{si }t=0\end{array}\right.$

On sait que l’intégrale impropre $\int_{0}^{+\infty}\dfrac{\sin\left(t\right)}{t}\thinspace dt$ est semi-convergente et ce qui précède montre que :

$\lim_{x\rightarrow0^{+}}\int_{0}^{+\infty}e^{-xt}\thinspace\dfrac{\sin\left(t\right)}{t}\thinspace dt=\int_{0}^{+\infty}\dfrac{\sin\left(t\right)}{t}\thinspace dt$

Mais on peut aussi dériver sous le signe somme (justification à la charge du lecteur) … Pour tout $x>0$ :

$\begin{eqnarray*}\dfrac{d}{dx}\int_{0}^{+\infty}e^{-xt}\thinspace\dfrac{\sin\left(t\right)}{t}\thinspace dt & = & -\int_{0}^{+\infty}e^{-xt}\thinspace\sin\left(t\right)\thinspace dt\\& = & -\dfrac{1}{1+x^{2}}\end{eqnarray*}$

Il en résulte qu’il existe $C\in\mathbb{R}$ tel que :

$\forall x>0,\thinspace\int_{0}^{+\infty}e^{-xt}\thinspace\dfrac{\sin\left(t\right)}{t}\thinspace dt=C-\arctan\left(x\right)$

Comme :

$\left|\int_{0}^{+\infty}e^{-xt}\thinspace\dfrac{\sin\left(t\right)}{t}\thinspace dt\right|\leqslant\int_{0}^{+\infty}e^{-xt}\thinspace dt=\dfrac{1}{x}$

on voit que :

$\lim_{x\rightarrow+\infty}\int_{0}^{+\infty}e^{-xt}\thinspace\dfrac{\sin\left(t\right)}{t}\thinspace dt=0$

et donc $C=\dfrac{\pi}{2}.$ Pour finir, grâce à la continuité en $0$ de $x\mapsto\int_{0}^{+\infty}e^{-xt}\thinspace\dfrac{\sin\left(t\right)}{t}\thinspace dt,$ il vient :

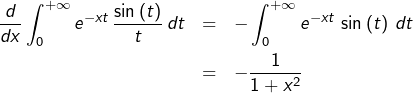
$\boxed{\int_{0}^{+\infty}\dfrac{\sin\left(t\right)}{t}\thinspace dt=\dfrac{\pi}{2}}$

Remarque 1

Dans ce calcul, il était essentiel de prouver la continuité de $F$ en $0.$ On aurait pu établir la continuité de $F$ sur $\left]0,+\infty\right[$ à moindre frais, car il suffit de prouver la convergence uniforme de la suite $\left(F_{n}\right)_{n\geqslant0}$ sur $\left[a,+\infty\right[$ pour tout $a>0,$ ce qui s’obtient par une majoration directe. En effet, pour tout $n\in\mathbb{N}$ et tout $x\in\left[a,+\infty\right[$ :

$\begin{eqnarray*}\left|F\left(x\right)-F_{n}\left(x\right)\right| & = & \left|\int_{n}^{+\infty}e^{-xt}\dfrac{\sin\left(t\right)}{t}\thinspace dt\right|\\& \leqslant & \int_{n}^{+\infty}e^{-xt}\thinspace dt\\& \leqslant & \int_{n}^{+\infty}e^{-at}\thinspace dt\\& = & \dfrac{e^{-an}}{a}\underset{n\rightarrow\infty}{\longrightarrow}0\end{eqnarray*}$

Mais bien sûr, cela ne permet pas de calculer l’intégrale de Dirichlet $\int_0^{+\infty}\frac{\sin(t)}{t}\,dt$ …

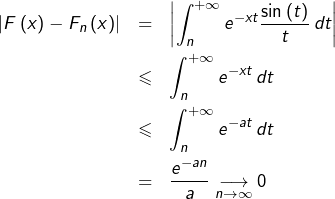
Remarque 2

Si, dans l’énoncé de l’exemple 2, l’hypothèse de semi-convergence de l’intégrale impropre $\int_{0}^{+\infty}f\left(t\right)\thinspace dt$ est remplacée par l’hypothèse plus forte d’absolue convergence, la continuité de $F$ est beaucoup plus simple à établir. En effet, pour tout $n\in\mathbb{N}$ et pour tout $x\geqslant0$ :

$\begin{eqnarray*}\left|F\left(x\right)-F_{n}\left(x\right)\right| & = & \left|\int_{n}^{+\infty}e^{-xt}\thinspace f\left(t\right)\thinspace dt\right|\\& \leqslant & \int_{n}^{+\infty}\left|f\left(t\right)\right|\thinspace dt\underset{n\rightarrow\infty}{\longrightarrow}0\end{eqnarray*}$

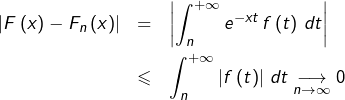
Pour toutes questions ou remarques, merci d’utiliser le formulaire de contact.

Partager cet article

Cet article a 2 commentaires

Abdellaziz harrabi 16 Déc 2024 Répondre

Sublime ! Une analyse prodigieuse; j’ai appris des techniques pertinentes.
CAMBOU 19 Août 2023 Répondre

L’exemple 1 est une question classique mais qui est super traitée .
Super et continuez !
C’est un plaisir de lire vos articles