Solutions détaillées de neuf exercices sur les suites numériques (fiche 01).
Cliquer ici pour accéder aux énoncés.


Si la formule de récurrence qui définit la suite ![]() ne comportait pas le terme
ne comportait pas le terme ![]() ce serait facile, car on aurait affaire à une suite géométrique de raison
ce serait facile, car on aurait affaire à une suite géométrique de raison ![]()
Tâchons de nous ramener à cette situation.
Notons ![]() l’unique réel vérifiant
l’unique réel vérifiant ![]() , autrement dit :
, autrement dit :
![Rendered by QuickLaTeX.com \[\boxed{\lambda=-\frac{3}{4}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a5cbae35c5c972da32896897e89705a3_l3.png)
En soustrayant membre à membre les égalités :
![Rendered by QuickLaTeX.com \[ \left\{\begin{array}{ccc}u_{n+1} & = & {\displaystyle\frac{u_{n}}{3}-\frac{1}{2}}\\\\\lambda & = & {\displaystyle\frac{\lambda}{3}-\frac{1}{2}}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d5da3e8a2eb0b93e195a99415ed0bb9d_l3.png)
![]()
Ceci prouve que la suite ![]() définie par :
définie par :
![]()
est géométrique de raison
![]()
![Rendered by QuickLaTeX.com \[ \boxed{\forall n\in\mathbb{N},\thinspace u_{n}=-\frac{1}{4\times3^{n}}-\frac{3}{4}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-49ea40ebcd6c142bdfde8e09dd62e541_l3.png)
En particulier, la suite ![]() converge vers
converge vers ![]()

Par hypothèse, on a pour tout ![]() :
:
![]()
![]()
![]()
D’après ![]() la suite
la suite ![]() est constante. Donc :
est constante. Donc :
![]()
Et d’après ![]() la suite
la suite ![]() est géométrique de raison
est géométrique de raison ![]() Donc :
Donc :
![]()
Avec ces deux formules en poche, on calcule aisément ![]() et
et ![]() (en effectuant la demi-somme et la demi-différence) :
(en effectuant la demi-somme et la demi-différence) :
![Rendered by QuickLaTeX.com \[ \boxed{\forall n\in\mathbb{N},\thinspace\left\{\begin{array}{ccc}a_{n} & = & \frac{1}{2}\left(r+s+\left(1-2p\right)^{n}\left(r-s\right)\right)\\\\b_{n} & = & \frac{1}{2}\left(r+s-\left(1-2p\right)^{n}\left(r-s\right)\right)\end{array}\right.}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cf20324d398f12da71d0c94b8103f3b6_l3.png)
On peut à présent conclure.
Comme ![]() alors
alors ![]() et donc
et donc ![]()
Ainsi, les suites ![]() et
et ![]() convergent, toutes les deux, vers
convergent, toutes les deux, vers ![]()

Pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[ q_{n+1}=1+\prod_{i=0}^{n}q_{i}=1+q_{n}\prod_{i=0}^{n-1}q_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-93c5a8eea4233103cd8207c7d25a00ec_l3.png)
![]()
Si l’on note, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[ S_{n}=\sum_{i=0}^{n-1}\frac{1}{q_{i}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-06fbb3055d62ba6e915db652614d7714_l3.png)
![]()
![]()
On remarque qu’il s’agit de fractions de plus en plus voisines de 1. Plus précisément, il semble bien que, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\boxed{S_{n}=1-\frac{1}{q_{n}-1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1a5d483966bb56ddeac1ba66fa244cc6_l3.png)
Montrons ceci par récurrence. Comme on vient de le voir, cette propriété est vraie pour ![]() ; on peut donc passer directement à l’hérédité.
; on peut donc passer directement à l’hérédité.
Supposons la formule vraie pour un certain ![]() . On calcule :
. On calcule :
![]()
![]()

Tout d’abord, cette suite est bien définie et à termes strictement positifs. Du coup, ![]() pour tout
pour tout ![]() En cas de convergence vers un réel
En cas de convergence vers un réel ![]() un passage à la limite dans cette inégalité montre que
un passage à la limite dans cette inégalité montre que ![]() (et, en particulier :
(et, en particulier : ![]()
En passant à la limite dans la formule de récurrence, on voit aussi que :
![]()
![]()
![]()
Mais la première de ces deux valeurs est exclue car négative. Bref : la convergence de la suite ![]() n’est toujours pas établie, mais si elle a lieu, c’est nécessairement vers le nombre d’or, que nous notons désormais
n’est toujours pas établie, mais si elle a lieu, c’est nécessairement vers le nombre d’or, que nous notons désormais ![]() :
:
![Rendered by QuickLaTeX.com \[\boxed{\gamma=\frac{1+\sqrt{5}}{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a2dacdc9e4ed9ce476595119ab7b4d70_l3.png)

Le principal intérêt de ce qui précède est de nous éclairer sur la valeur de la seule limite possible.
Prouvons maintenant la convergence de cette suite. Pour tout ![]() :
:
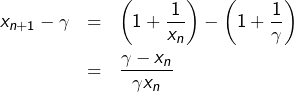
donc, vu que
![]()
![]()
Comme ![]() cette dernière majoration permet de conclure que :
cette dernière majoration permet de conclure que :
![]()
![Rendered by QuickLaTeX.com \[ \boxed{\lim_{n\rightarrow\infty}x_{n}=\frac{1+\sqrt{5}}{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e657a182e5388899cdf02a4a778035ae_l3.png)
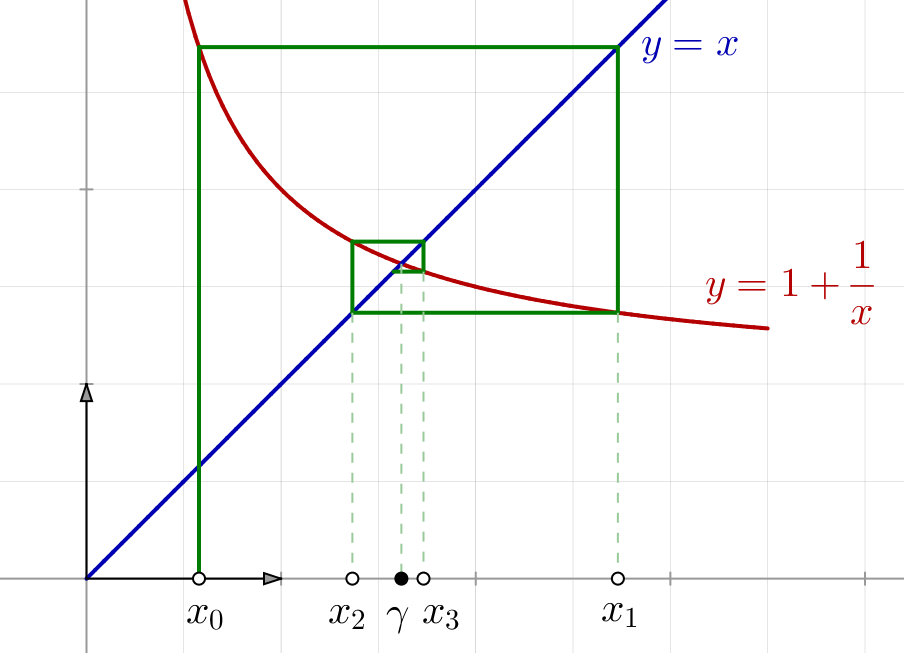
L’illustration ci-dessous montre le calcul des premiers termes :

Pour tout ![]() :
:
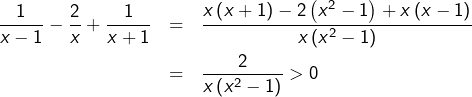
d’où :
![]()
![Rendered by QuickLaTeX.com \[ \sum_{k=1}^{n}\left(\frac{1}{3k-1}+\frac{1}{3k}+\frac{1}{3k+1}\right)>\sum_{k=1}^{n}\frac{1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8600e795a8e32bc1b94ee62586347816_l3.png)
![]()
On attribue cette méthode à Pietro Mengoli ![]() Elle évoque une preuve plus classique, qui repose sur le fait que, pour tout
Elle évoque une preuve plus classique, qui repose sur le fait que, pour tout ![]() :
:
![]()

La relation
![]()
![]()
![Rendered by QuickLaTeX.com \[ \frac{y_{n}}{n!}-y_{0}=\sum_{k=0}^{n-1}\frac{1}{\left(k+1\right)!}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4f04e9085013723997e9f19f12374ec3_l3.png)
![Rendered by QuickLaTeX.com \[y_{n}=n!\sum_{k=1}^{n}\frac{1}{k!}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d484a7f2bffa8b1f4477b250bbcd9f6e_l3.png)
Or, il est bien connu que, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[ \lim_{n\rightarrow\infty}\sum_{k=0}^{n}\frac{t^{k}}{k!}=e^{t}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-04e86a2e1acbe7c16967ea0a75cd6742_l3.png)
![]()

L’hypothèse :
![]()
peut s’écrire :
![]()
Comme la suite ![]() est convergente, elle est nécessairement bornée. Et comme la suite
est convergente, elle est nécessairement bornée. Et comme la suite ![]() est bornée par hypothèse, on voit que
est bornée par hypothèse, on voit que ![]() l’est aussi et elle est en particulier minorée.
l’est aussi et elle est en particulier minorée.
On invoque alors le théorème de la limite monotone : la suite ![]() est décroissante est minorée, donc convergente.
est décroissante est minorée, donc convergente.
Pour finir, la suite ![]() est convergente puisque c’est la somme de deux suites convergentes.
est convergente puisque c’est la somme de deux suites convergentes.

On passe au logarithme :
![Rendered by QuickLaTeX.com \[ \ln\left(P_{n}\right)=\frac{1}{n}\sum_{k=1}^{n}\ln\left(n^{2}+k^{2}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-695aedf927ffe21976a4581864fcd243_l3.png)
c’est-à-dire :
![Rendered by QuickLaTeX.com \[ \ln\left(P_{n}\right)=\frac{1}{n}\sum_{k=1}^{n}\left[2\ln\left(n\right)+\ln\left(1+\frac{k^{2}}{n^{2}}\right)\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-205e23dd6f48b616d1a36119393adc61_l3.png)
ou encore :
![]()
où l’on a posé :
![Rendered by QuickLaTeX.com \[ R_{n}=\frac{1}{n}\sum_{k=1}^{n}\ln\left(1+\frac{k^{2}}{n^{2}}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4634d9b88cda68e898a21e60f659a975_l3.png)
On reconnaît une somme de Riemann attachée à l’application ![]() Par conséquent :
Par conséquent :
![]()
Si l’on intègre par parties en posant :
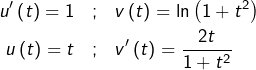
ce qui donne :
![Rendered by QuickLaTeX.com \begin{eqnarray*}\int_{0}^{1}\ln\left(1+t^{2}\right)\thinspace dt & = & \left[t\ln\left(1+t^{2}\right)\right]_{0}^{1}-2\int_{0}^{1}\frac{t^{2}}{1+t^{2}}\thinspace dt\\& = & \ln\left(2\right)-2\int_{0}^{1}\left(1-\frac{1}{1+t^{2}}\right)\thinspace dt\\& = & \ln\left(2\right)-2\left(1-\frac{\pi}{4}\right)\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-a98526d523a872d1dd832c17e5f1326f_l3.png)
Notons ![]() cette valeur. On a montré, à ce stade que lorsque
cette valeur. On a montré, à ce stade que lorsque ![]() :
:
![]()
![]()
ou, de façon plus explicite :
![]()

Vues les hypothèses :
![]()
Or, on sait (par convexité de l’exponentielle ou par une preuve directe) que :
![]()
Il en résulte que :
![Rendered by QuickLaTeX.com \[\begin{array}{ccc}{\displaystyle \lim_{n\rightarrow\infty}\left(e^{a_{n}}-1-a_{n}\right)} & = & 0\\\\{\displaystyle \lim_{n\rightarrow\infty}\left(e^{b_{n}}-1-b_{n}\right)} & = & 0\\\\{\displaystyle \lim_{n\rightarrow\infty}\left(e^{c_{n}}-1-c_{n}\right)} & = & 0\end{array}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c9f55d120603dd0bc0dd4718b1178fb9_l3.png)
Montrons que ceci entraîne :
![Rendered by QuickLaTeX.com \[\begin{array}{ccc}{\displaystyle \lim_{n\rightarrow\infty}a_{n}} & = & 0\\\\{\displaystyle \lim_{n\rightarrow\infty}b_{n}} & = & 0\\\\{\displaystyle \lim_{n\rightarrow\infty}c_{n}} & = & 0\end{array}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f8add84b0730b3d0f835315881f5e562_l3.png)
On observe que l’application
![]()
induit :
➭ une bijection décroissante ![]()
➭ une bijection croissante ![]()
Etant donné ![]() si
si ![]() vérifie
vérifie ![]() alors de deux choses l’une :
alors de deux choses l’une :
- ou bien
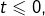 auquel cas
auquel cas 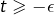
- ou bien
 auquel cas
auquel cas 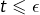
et par conséquent : ![]()
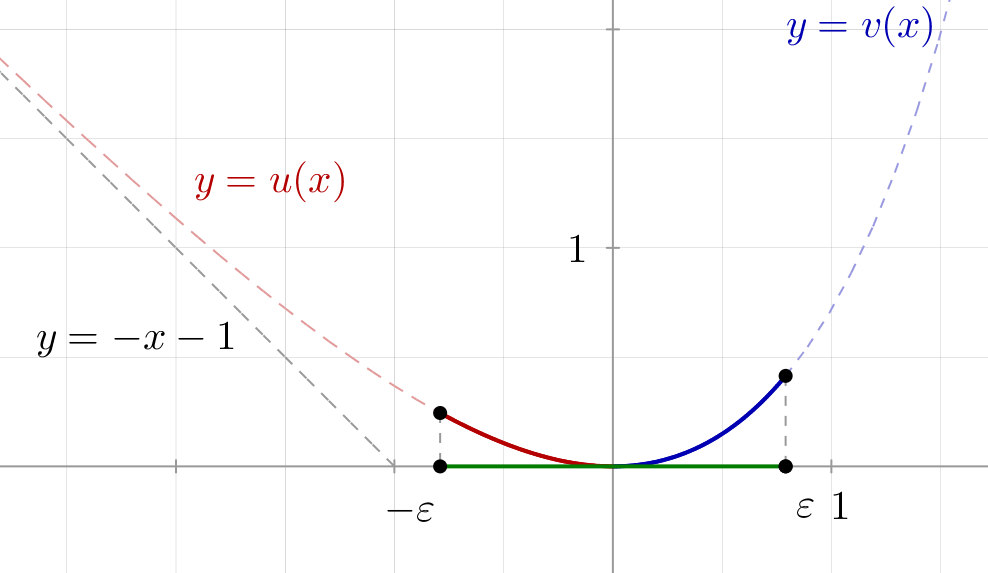
Comme ![]() , il existe
, il existe ![]() tel que :
tel que :
![]()
Ainsi : ![]() et le même argument s’applique aux deux autres suites.
et le même argument s’applique aux deux autres suites.
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
