Neuf énoncés d’exercices sur les séries numériques (fiche 03).

On considère deux séries complexes : ![]() est absolument convergente et
est absolument convergente et ![]() est semi-convergente. Prouver que, pour tout
est semi-convergente. Prouver que, pour tout ![]() la série
la série ![]() est convergente.
est convergente.

Calculer, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[S_{p}=\sum_{n=1}^{\infty}\frac{1}{n\left(n+p\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-53e6541895dadb9e36b5ad5c85ce7040_l3.png)

Préciser la nature de la série de terme général :
![]()

On pose, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[u_{n}=\left\{ \begin{array}{cc}\displaystyle{\frac{1}{n}} & \text{si }n\text{ est un carré}\\\\\displaystyle{\frac{1}{n^{2}}} & \text{sinon}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8bbc73365e1191f8de4da6d0ca706bac_l3.png)

Etudier, en fonction du couple ![]() la nature de la série :
la nature de la série :
![Rendered by QuickLaTeX.com \[\sum_{n\geqslant2}\frac{1}{n^{\alpha}\ln^{\beta}\left(n\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-caff37d89d5cf4d80067f516f9457f44_l3.png)

Prouver que si ![]() et
et ![]() alors la série
alors la série 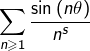 est semi-convergente.
est semi-convergente.

On considère une série complexe convergente ![]() Etudier la nature de la série
Etudier la nature de la série ![]()

On pose, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[S_{n}=\sum_{k=0}^{n}\frac{1}{k!}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2d98baf98661fdbc6ce507245e8512e9_l3.png)
- Montrer que la suite
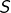 est convergente et préciser sa limite. On pose désormais :
est convergente et préciser sa limite. On pose désormais :![Rendered by QuickLaTeX.com \[R_{n}=\sum_{k=n+1}^{\infty}\frac{1}{k!}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-eb121700223337e62f296211d0b4837f_l3.png)
- Montrer que :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N}^{\star},\thinspace\frac{1}{\left(n+1\right)!}\leqslant R_{n}\leqslant\frac{1}{n\thinspace n!}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-852a3c2ba22ad5b75f1331922468455c_l3.png)
- Montrer que la série
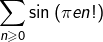 est convergente.
est convergente.

Soient ![]() et
et ![]() deux séries complexes. On suppose que la première est absolument convergente et que la seconde est semi-convergente. Montrer que leur produit de Cauchy converge et préciser sa somme.
deux séries complexes. On suppose que la première est absolument convergente et que la seconde est semi-convergente. Montrer que leur produit de Cauchy converge et préciser sa somme.
Cliquer ici pour accéder aux indications
Cliquer ici pour accéder aux solutions

