icone-math-OS-Exos
exercice 1 facile

Comme la série \sum_{n\geqslant0}b_{n} converge, la suite b converge vers 0 : elle est en particulier bornée.

Notons M>0 tel que :

    \[\forall n\in\mathbb{N},\thinspace\left|b_{n}\right|\leqslant M\]

Alors, étant donné p\in\mathbb{N} :

    \[\forall n\in\mathbb{N},\thinspace\left|a_{n}\left(b_{n}\right)^{p}\right|\leqslant M^{p}\left|a_{n}\right|\]

ce qui montre la convergence absolue (et donc la convergence tout court) de la série \sum_{n\geqslant0}a_{n}\left(b_{n}\right)^{p}.

Remarque

Si les deux séries \sum_{n\geqslant0}a_{n} et \sum_{n\geqslant0}b_{n} sont supposées semi-convergentes, alors la convergence de la série \sum_{n\geqslant0}a_{n}\left(b_{n}\right)^{p} n’est plus assurée en général.

Contre-exemple :

    \[a_{n}=b_{n}=\frac{\left(-1\right)^{n}}{\sqrt{n+1}}\qquad\text{et}\qquad p=1\]

En effet, dans ce cas :

    \[a_{n}b_{n}=\frac{1}{n+1}\]

et l’on sait bien que la série harmonique diverge.

exercice 2 facile

Pour tout n\in\mathbb{N}^{\star} :

    \[\frac{1}{n\left(n+p\right)}=\frac{1}{p}\left(\frac{1}{n}-\frac{1}{n+p}\right)\]

et donc :

    \begin{eqnarray*}\sum_{n=1}^{N}\frac{1}{n\left(n+p\right)} & = & \frac{1}{p}\sum_{n=1}^{N}\left(\frac{1}{n}-\frac{1}{n+p}\right)\\& = & \frac{1}{p}\sum_{n=1}^{N}\sum_{k=1}^{p}\left(\frac{1}{n+k-1}-\frac{1}{n+k}\right)\\& = & \frac{1}{p}\sum_{k=1}^{p}\sum_{n=1}^{N}\left(\frac{1}{n+k-1}-\frac{1}{n+k}\right)\\& = & \frac{1}{p}\sum_{k=1}^{p}\left(\frac{1}{k}-\frac{1}{N+K}\right)\\& = & \frac{1}{p}\sum_{k=1}^{p}\frac{1}{k}-\frac{1}{p}\sum_{k=1}^{p}\frac{1}{N+K}\end{eqnarray*}

En faisant tendre N vers +\infty, on conclut que :

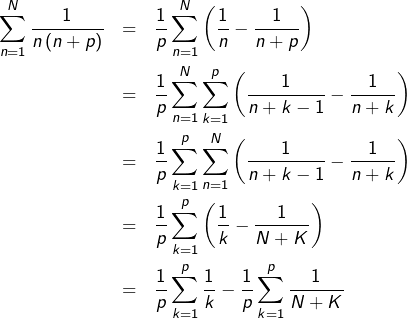
    \[\fcolorbox{black}{myBlue}{$\displaystyle{\sum_{n=1}^{\infty}\frac{1}{n\left(n+p\right)}=\frac{1}{p}\sum_{k=1}^{p}\frac{1}{k}}$}\]

Cette formule a été établie, dans des cas particulier, par Pietro Mengoli en 1650. A ce sujet, on pourra consulter cette vidéo.

On utilise le fait que :

    \[\forall x\geqslant0,\thinspace\frac{1}{1+x}\geqslant1-x\]

pour obtenir, pour tout n\in\mathbb{N} et pour tout t\in\left[0,1\right] :

    \[\frac{t^{n}}{1+t^{n}}\geqslant t^{n}\left(1-t^{n}\right)=t^{n}-t^{2n}\]

et donc :

    \[u_{n}\geqslant\frac{1}{n+1}-\frac{1}{2n+1}=\frac{n}{\left(n+1\right)\left(2n+1\right)}\underset{\text{def}}{=}a_{n}\]

Or, la série \sum_{n\geqslant0}a_{n} est divergente comme le prouve l’équivalent :

    \[a_{n}\sim\frac{1}{2n}\]

Par conséquent, la série \sum_{n\geqslant0}u_{n} diverge aussi.

Posons pour tout n\geqslant1 :

    \[S_{n}=\sum_{k=1}^{n}u_{k}\]

Alors :

    \[S_{n^{2}}=\sum_{q=1}^{n}\frac{1}{q^{2}}+\sum_{{1\leqslant k\leqslant n^{2}\atop k\text{ non carré}}}\frac{1}{k^{2}}\leqslant2\thinspace\sum_{k=1}^{\infty}\frac{1}{k^{2}}\]

Comme la suite S est croissante (sommes partielles d’une série à termes positifs), l’existence d’une suite extraite majorée montre que S est elle-même majorée, donc convergente. On voit en outre que :

    \[\sum_{{1\leqslant k\leqslant n^{2}\atop k\text{ non carré}}}\frac{1}{k^{2}}=\sum_{k=1}^{n^{2}}\frac{1}{k^{2}}-\sum_{k=1}^{n}\frac{1}{k^{4}}\rightarrow\zeta\left(2\right)-\zeta\left(4\right)\]

Finalement :

    \[\sum_{n=1}^{\infty}u_{n}=2\thinspace\zeta\left(2\right)-\zeta\left(4\right)=\fcolorbox{black}{myBlue}{$\displaystyle{\frac{\pi^{2}}{3}-\frac{\pi^{4}}{90}}$}\]

Ces séries sont connues sous le nom de séries de Bertrand. Elles sont considérées comme des séries de références (au même titre que les séries géométriques ou les séries de Riemann).

Notons, pour tout n\geqslant2 :

    \[u_{n}=\frac{1}{n^{\alpha}\ln^{\beta}\left(n\right)}\]

et distinguons trois cas.

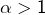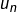  • Supposons \alpha>1 et soit \lambda\in\left]1,\alpha\right[. En écrivant u_{n} sous la forme :

        \[u_{n}=A_{n}\;\frac{1}{n^{\lambda}}\qquad\text{avec : }A_{n}=\frac{1}{n^{\alpha-\lambda}\ln^{\beta}\left(n\right)}\]

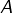    on constate que la suite A est majorée par 1 APCR (puisqu’elle converge vers 0 d’après la propriété des croissances comparées). La série 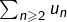\sum_{n\geqslant2}u_{n} est donc convergente, par comparaison avec une série de Riemann.
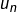  • Supposons \alpha<1 et soit \mu\in\left]\alpha,1\right[. En écrivant u_{n} sous la forme :

        \[u_{n}=B_{n}\:\frac{1}{n^{\mu}}\qquad\text{avec : }B_{n}=\frac{1}{n^{\alpha-\mu}\ln^{\beta}\left(n\right)}\]

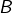    on constate que la suite B est minorée par 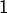1 APCR (puisqu’elle diverge vers l’infini, d’après la propriété des croissances comparées). La série 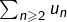\sum_{n\geqslant2}u_{n} est donc divergente, par comparaison avec une série de Riemann.
  • Enfin, si 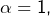\alpha=1, on compare avec un intégrale. Pour tout n\geqslant2 :

        \[\frac{1}{n\ln\left(n\right)}\geqslant\int_{n}^{n+1}\frac{1}{t\ln\left(t\right)}\thinspace dt\]

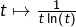    car l’application t\mapsto\frac{1}{t\ln\left(t\right)} décroît sur 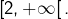\left[2,+\infty\right[. Après sommation :

        \[\sum_{k=2}^{n}\frac{1}{k\ln\left(k\right)}\geqslant\int_{2}^{n+1}\frac{1}{t\ln\left(t\right)}\thinspace dt=\ln\left(\ln\left(n+1\right)\right)-\ln\left(\ln\left(2\right)\right)\]

    Il s’ensuit que :

        \[\lim_{n\rightarrow\infty}\sum_{k=2}^{n}\frac{1}{k\ln\left(k\right)}=+\infty\]

Remarque

Une proposition analogue concernant des intégrales impropres, est présentée dans cet article.

Soient \theta\in\mathbb{R}-\pi\mathbb{Z} et s\in\left]0,1\right].
On sait (voir cet article \url{https://math-os.com/series-numeriques-partie-2/#section-5} pour les détails) que la série :

    \[\sum_{n\geqslant1}\frac{e^{in\theta}}{n^{s}}\]

converge. Et comme :

    \[\frac{\sin\left(n\theta\right)}{n^{s}}=\text{Im}\left(\frac{e^{in\theta}}{n^{s}}\right)\]

la série :

    \[\sum_{n\geqslant1}\frac{\sin\left(n\theta\right)}{n^{s}}\]

converge aussi. Montrons sa semi-convergence. D’après l’inégalité t\geqslant t^{2}, valable pour tout t\in\left[0,1\right], on voit que pour tout n\geqslant1 :

    \[\left|\frac{\sin\left(n\theta\right)}{n^{s}}\right|\geqslant\frac{\sin^{2}\left(n\theta\right)}{n^{s}}=\frac{1-\cos\left(2n\theta\right)}{2n^{s}}\underset{\text{def}}{=}u_{n}\]

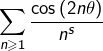Or, la série {\displaystyle \sum_{n\geqslant1}\frac{1}{n^{s}}} diverge et la série {\displaystyle \sum_{n\geqslant1}\frac{\cos\left(2n\theta\right)}{n^{s}}} converge (car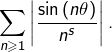 2\theta\in\mathbb{R}-2\pi\mathbb{Z}), ce qui entraîne la divergence de la série {\displaystyle \sum_{n\geqslant1}u_{n},} et donc (d’après le principe de comparaison) la divergence de la série {\displaystyle \sum_{n\geqslant1}\left|\frac{\sin\left(n\theta\right)}{n^{s}}\right|.}

Il suffit d’appliquer la règle d’Abel. En effet, la suite \left(\frac{1}{n}\right)_{n\geqslant1} converge vers 0 en décroissant et la suite de terme général :

    \[ S{n}=\sum_{k=1}^{n}u_{k}\]

est bornée puisque convergente.

Bon. Tous comptes faits, cet exercice aurait mérité un petit pictogramme vert. C’est juste l’intervention de la règle d’Abel qui m’a fait hésiter …

Question 1

La série {\displaystyle \sum_{n\geqslant0}\frac{1}{n!}} converge d’après la règle de d’Alembert. En effet, si l’on pose u_{n}=\frac{1}{n!}, alors pour tout n\in\mathbb{N} :

    \[\frac{u_{n+1}}{u_{n}}=\frac{\frac{1}{\left(n+1\right)!}}{\frac{1}{n!}}=\frac{1}{n+1}\]

et donc {\displaystyle \lim_{n\rightarrow\infty}\frac{u_{n+1}}{u_{n}}=0<1.}
Pour calculer sa somme, appliquons la formule de Taylor avec reste intégral à la fonction exponentielle. Pour tout n\in\mathbb{N} et pour tout x\in\mathbb{R} :

    \[e^{x}=\sum_{k=0}^{n}\frac{x^{k}}{k!}+\int_{0}^{x}\frac{\left(x-t\right)^{n}}{n!}\thinspace e^{t}\thinspace dt\]

Donc, en choisissant x=1, il vient :

    \[e=S_{n}+I_{n}\]

où l’on a posé :

    \[S_{n}=\sum_{k=0}^{n}\frac{1}{k!}\qquad\text{et}\qquad I_{n}=\int_{0}^{1}\frac{\left(1-t\right)^{n}}{n!}\thinspace e^{t}\thinspace dt\]

Or :

    \[0\leqslant I_{n}\leqslant\frac{e}{n!}\thinspace\int_{0}^{1}\left(1-t\right)^{n}\thinspace dt=\frac{e}{\left(n+1\right)!}\]

Ceci prouve que {\displaystyle \lim_{n\rightarrow\infty}I_{n}=0}. Il s’ensuit que :

    \[\fcolorbox{black}{myBlue}{$\displaystyle{\sum_{k=0}^{\infty}\frac{1}{k!}=e}$}\]

Remarque 1

La preuve préalable de la convergence via la règle de d’Alembert était superflue, puisque la suite du calcul prouve la convergence (et donne en prime la valeur de la somme).

Remarque 2

On notera que I_{n}=R_{n}, où :

    \[R_{n}=\sum_{k=n+1}^{\infty}\frac{1}{k!}\]

Autrement dit, la formule de Taylor avec reste intégral porte bien son nom : elle fournit, en cas de convergence de la série de Taylor, une expression intégrale du reste de celle-ci.

Remarque 3

D’une manière générale (et par une preuve similaire, reposant sur la formule de Taylor avec reste intégral) :

    \[\boxed{\forall x\in\mathbb{R},\thinspace e^{x}=\sum_{n=0}^{\infty}\frac{x^{n}}{n!}}\]

Question 2

D’évidence, le reste est minoré par son premier terme :

    \[R_{n}\geqslant\frac{1}{\left(n+1\right)!}\]

Par ailleurs, pour tout entier k\geqslant n+1 :

    \[\frac{1}{k!}=\frac{1}{\left(n+1\right)!}\thinspace\prod_{j=n+2}^{k}\frac{1}{j}\leqslant\frac{1}{n!}\:\frac{1}{\left(n+1\right)^{k-n-1}}\]

donc :

    \[R_{n}\leqslant\frac{1}{\left(n+1\right)!}\sum_{k=n+1}^{\infty}\frac{1}{\left(n+1\right)^{k-n-1}}=\frac{1}{\left(n+1\right)!}\sum_{k=0}^{\infty}\frac{1}{\left(n+1\right)^{k}}\]

Or on sait calculer cette dernière somme (série géométrique de raison \frac{1}{n+1}) :

    \[\sum_{k=0}^{\infty}\frac{1}{\left(n+1\right)^{k}}=\frac{1}{1-\frac{1}{n+1}}=\frac{n+1}{n}\]

de sorte que, finalement :

    \[R_{n}\leqslant\frac{1}{\left(n+1\right)!}\thinspace\frac{n+1}{n}=\frac{1}{n\thinspace n!}\]

Bref, on a prouvé que :

    \[\boxed{\forall n\in\mathbb{N}^{\star},\thinspace\frac{1}{\left(n+1\right)!}\leqslant R_{n}\leqslant\frac{1}{n\thinspace n!}}\]

Question 3

Avec les notations introduits précédemment, à savoir :

    \[S_{n}=\sum_{k=0}^{n}\frac{1}{k!}\qquad\text{et}\qquad R_{n}=\sum_{k=n+1}^{\infty}\frac{1}{k!}\]

on a pour tout n\in\mathbb{N} :

    \[en!=n!\left(S_{n}+R_{n}\right)\]

Or, on observe que :

    \[n!\thinspace S_{n}=\sum_{k=0}^{n}\frac{n!}{k!}=n+1+P_{n}\]

où P_{n} est un entier pair, ce qui montre que n!\thinspace S_{n} est un entier que même parité que n+1. Il en résulte que :

    \[\sin\left(\pi en!\right)=\left(-1\right)^{n+1}\sin\left(\pi n!R_{n}\right)\]

Par ailleurs :

    \[\frac{\left(n+1\right)!R_{n+1}}{n!R_{n}}=\left(n+1\right)\thinspace\frac{R_{n+1}}{R_{n}}\leqslant\left(n+1\right)\thinspace\frac{\frac{1}{\left(n+1\right)\left(n+1\right)!}}{\frac{1}{\left(n+1\right)!}}=1\]

ce qui prouve que la suite \left(n!\thinspace R_{n}\right)_{n\geqslant1} décroît (et converge vers 0 puisque 0{n}\leqslant\frac{1}{n}). Comme cette suite est valeurs dans \left[0,\frac{1}{2}\right] à partir du rang 2, et vu que \sin est croissante sur \left[0,\frac{\pi}{2}\right], on en déduit que la suite \left(\sin\left(\pi n!R_{n}\right)\right){n\geqslant2} converge vers 0 en décroissant. Le théorème des séries alternées s’applique donc : la série {\displaystyle \sum{n\geqslant0}\sin\left(\pi en!\right)} est convergente.

exercice 9 difficile

Le résultat établi dans cet exercice est connu sous le nom de théorème de Mertens.

Notons pour tout n\in\mathbb{N} :

    \[A_{n}=\sum_{k=0}^{n}a_{k}\qquad B_{n}=\sum_{k=0}^{n}b_{k},\qquad A'_{n}=\sum_{k=0}^{n}\left|a'_{k}\right| \]

    \[X_{n}=\sum_{k=0}^{n}\left(\sum_{j=0}^{k}a_{j}b_{k-j}\right)\]

ainsi que : \Delta_{n}=X_{2n}-A_{n}B_{n}.

D’une part :

    \[\boxed{A_{n}B_{n}=\sum_{\left(i,j\right)\in C}a_{i}b_{j}}\]

avec :

    \[C=\left\{ \left(i,j\right)\in\mathbb{N}^{2};\thinspace i\leqslant n\text{ et }j\leqslant n\right\}\]

et d’autre part :

    \[\boxed{X_{2n}=\sum_{\left(i,j\right)\in T}a_{i}b_{j}}\]

avec :

    \[T=\left\{ \left(i,j\right)\in\mathbb{N}^{2};\thinspace i+j\leqslant2n\right\}\]

Donc :

    \[\boxed{\Delta_{n}=\sum_{\left(i,j\right)\in W}a_{i}b_{j}}\]

avec :

    \[W=T-C\]

La figure ci-dessous montre à quoi ressemblent les domaines de sommation C, T et W (Attention : une coloration unie ne doit pas faire oublier qu’il s’agit d’ensembles finis !) :

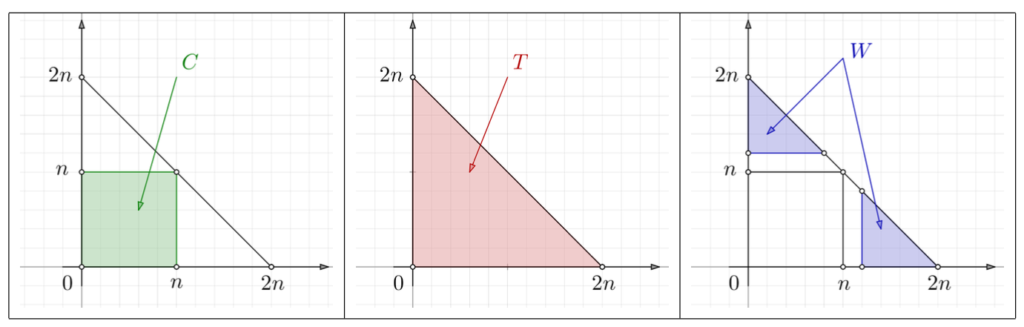
De manière plus explicite :

    \begin{eqnarray*}\Delta_{n} & = & \left[a_{0}\left(b_{n+1}+\cdots+b_{2n}\right)+\cdots+a_{n-2}\left(b_{n+1}+b_{n+2}\right)+a_{n-1}b_{n+1}\right]+\\& & \qquad\left[a_{n+1}\left(b_{0}+\cdots+b_{n-1}\right)+\cdots+a_{2n-1}\left(b_{0}+b_{1}\right)+a_{2n}b_{0}\right]\end{eqnarray*}

Soit \varepsilon>0. Vues les hypothèses, il existe un entier N tel que :

    \[\forall n\geqslant N,\forall p\geqslant1\:\left|b_{n+1}+\cdots+b_{n+p}\right|\leqslant\varepsilon\]

    \[\forall n\geqslant N,\forall p\geqslant1\:\left|a_{n+1}\right|+\cdots+\left|a_{n+p}\right|\leqslant\varepsilon\]

De plus, les sommes partielles A_{n}' et B_{n} sont bornées puisque convergentes :

    \[\left(\exists\lambda>0;\thinspace\forall n\in\mathbb{N},\,\left|A_{n}'\right|\leqslant\lambda\right)\textrm{ et }\left(\exists\mu>0;\,\forall n\in\mathbb{N},\,\left|B_{n}\right|\leqslant\mu\right)\]

Ainsi, dès que n\geqslant N :

    \[\left|\Delta_{n}\right|\leqslant\varepsilon\left(\lambda+\mu\right)\]

et ceci prouve que la suite \left(X_{2n}\right)_{n\geqslant0} converge vers AB. Comme X_{2n+1}=X_{2n}+x_{2n+1}, il en va de même pour \left(X_{2n+1}\right)_{n\geqslant0} grâce au lemme ci-après. En conclusion :

    \[\fcolorbox{black}{myBlue}{$\displaystyle{\lim_{n\rightarrow\infty}\,X_{n}=AB}$}\]

Lemme

Si \sum a_{n} ACV et si {\displaystyle \lim_{n\rightarrow\infty}b_{n}=0,} alors {\displaystyle \lim_{n\rightarrow\infty}\sum_{k=0}^{n}a_{k}b_{n-k}=0}.

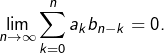
Preuve (cliquer pour déplier / replier)

Notons p_{n}=\left\lfloor \frac{n}{2}\right\rfloor . Etant donné \epsilon>0, il existe N\in\mathbb{N} tel que

    \[n\geqslant N\Rightarrow\sum_{k=1+p_{n}}^{n}\left|a_{k}\right|\leqslant\epsilon\]

Par ailleurs, il existe M\geqslant0 tel que :

    \[\forall n\in\mathbb{N},\,\sum_{k=0}^{n}\left|a_{k}\right|\leqslant M\]

Enfin, il existe N' tel que :

    \[n\geqslant N'\Rightarrow\left|b_{n}\right|\leqslant\epsilon\]

Dès que n\geqslant2N', on a :

    \[n-p_{n}\geqslant\frac{n}{2}\geqslant N'\]

et donc, dès que n\geqslant\max\left\{ N,2N'\right\} :

    \begin{eqnarray*}\left|\sum_{k=0}^{n}a_{k}b_{n-k}\right| & \leqslant & \sum_{k=0}^{p_{n}}\left|a_{k}\right|\left|b_{n-k}\right|+\sum_{k=1+p_{n}}^{n}\left|a_{k}\right|\left|b_{n-k}\right|\\& \leqslant & \epsilon\sum_{k=0}^{p_{n}}\left|a_{k}\right|+\left\Vert b\right\Vert_{\infty}\sum_{k=1+p_{n}}^{n}\left|a_{k}\right|\\& \leqslant & \left(M+\left\Vert b\right\Vert _{\infty}\right)\epsilon\end{eqnarray*}

ce qui établit le lemme.

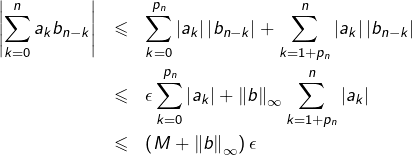
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.

Partager cet article
    

Laisser un commentaire