Indications - Exercices sur les séries numériques - 02

Indications pour démarrer les exercices sur les séries numériques (fiche 02).
Cliquer ici pour accéder aux énoncés.

A première vue, cet exercice paraît bien compliqué !

Mais à première vue seulement …

Quelle majoration très simple a-t-on pour $d_{n}$ ?

L’idée est de comparer la suite $\left(a_{n}\right)_{n\geqslant1}$ à une suite géométrique.

Il ne reste plus qu’à en trouver la raison …

Observer (en le justifiant) que ${\displaystyle \lim_{n\rightarrow+\infty}n^{\mu}e^{-\sqrt{n}}}=0,$ quel que soit l’exposant réel $\mu.$

Essayer de minorer cette intégrale par une intégrale plus facile à calculer.

En déduire la divergence de la série proposée.

Trouver la limite de $n\thinspace u_{n}$ ne devrait pas être difficile si vous connaissez le lemme de Cesàro.

Trouver un équivalent de $q_{n}$ lorsque $n$ tend vers $+\infty.$

On pourra commencer par effectuer un développement asymptotique à trois termes de $\cos\left(\frac{1}{n}\right).$

Déterminer un réel $\lambda$ tel que la suite $\left(x_{n+1}^{\lambda}-x_{n}^{\lambda}\right)_{n\geqslant0}$ converge vers une limite non nulle.

Appliquer alors le lemme de Cesàro pour obtenir un équivalent de $x_{n}$ lorsque $n\rightarrow+\infty.$ Ceci permettra de connaître la nature de la série $\sum_{n\geqslant0}x_{n}.$

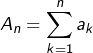En posant $A_{0}=0$ et $A_{n}=\sum_{k=1}^{n}a_{k}$ pour tout $n\geqslant1,$ vérifier que :

$\sum_{k=1}^{n}a_{k}b_{k}=A_{n}b_{n}+\sum_{k=1}^{n-1}A_{k}\left(b_{k}-b_{k+1}\right)$

Il restera alors à comprendre pourquoi le membre de droite de l’égalité ci-dessus admet une limite finie lorsque $n\to+\infty$ .

On pourra utiliser le résultat suivant (dont une variante a été étudiée à l’exercice précédent) :

Règle d’Abel

Si $\left(t_{n}\right)_{n\geqslant1}$ est une suite décroissante et de limite nulle et si $\left(x_{n}\right)_{n\geqslant1}$ est une suite (complexe) pour laquelle la suite des sommes partielles est bornée, c’est-à-dire :

$\exists M>0;\thinspace\forall n\in\mathbb{N}^{\star},\thinspace\left|\sum_{k=1}^{n}x_{k}\right|\leqslant M$

alors la série $\sum_{n\geqslant1}t_{n}x_{n}$ converge.

Cette version est expliquée en détails dans le corrigé de l’exercice n° 3 de cette fiche.

En choisissant judicieusement les suites $\left(t_{n}\right)_{n\geqslant1}$ et $\left(x_{n}\right)_{n\geqslant1},$ on peut produire un exemple de série convergente $\sum_{n\geqslant1}z_{n}$ telle que la série $\sum_{n\geqslant1}z_{n}^{3}$ diverge.

Partager cet article