Neuf énoncés d’exercices sur l’indépendance linéaire (fiche 01)

On définit trois applications ![]() sur
sur ![]() par :
par :
![Rendered by QuickLaTeX.com \[ \forall x\in\mathbb{R},\thinspace\left\{\begin{array}{ccc} f\left(x\right) & = & x\sin\left(x\right)\\ g\left(x\right) & = & x^{2}\sin\left(2x\right)\\ h\left(x\right) & = & x^{3}\sin\left(3x\right) \end{array}\right. \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3564a0edcc52cbf9563fdb03b89b908b_l3.png)
Montrer que la famille

On définit trois applications ![]() sur
sur ![]() par :
par :
![Rendered by QuickLaTeX.com \[ \forall\left(x,y\right)\in\mathbb{R}^{2},\thinspace\left\{\begin{array}{ccc} F\left(x,y\right) & = & \sin\left(2x+3y\right)\\ G\left(x,y\right) & = & \sin\left(x+2y\right)\cos\left(x+y\right)\\ H\left(x,y\right) & = & \cos\left(x+2y\right)\sin\left(x+y\right) \end{array}\right. \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-96aec755ae312106ea3f3e3b9ae295cb_l3.png)
La famille

Montrer que les trois applications ![]() définies sur
définies sur ![]() par :
par :
![Rendered by QuickLaTeX.com \[ \forall x\in\mathbb{R},\thinspace\left\{\begin{array}{ccc} f\left(x\right) & = & \sin\left(x+1\right)\\ g\left(x\right) & = & \sin\left(x+2\right)\\ h\left(x\right) & = & \sin\left(x+3\right) \end{array}\right. \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5bdb60f9c817e2e6754576149a8e65bc_l3.png)
forment une famille liée.

Soit ![]() un
un ![]() -espace vectoriel et soient
-espace vectoriel et soient ![]() trois vecteurs de
trois vecteurs de ![]()
- Vrai ou Faux ? Si
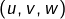 est libre, alors
est libre, alors 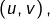
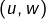 et
et 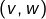 sont libres.
sont libres. - Vrai ou Faux ? Si
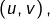
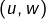 et
et 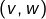 sont libres, alors
sont libres, alors 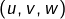 est libre.
est libre. - Vrai ou Faux ? Si
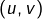 et
et 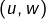 sont liées alors
sont liées alors 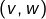 est liée.
est liée.
Soit ![]() un
un ![]() -espace vectoriel et soit
-espace vectoriel et soit ![]() un famille de
un famille de ![]() vecteurs.
vecteurs.
Montrer que si ![]() est libre et si
est libre et si ![]() est liée, alors
est liée, alors ![]()

Soient ![]() des
des ![]() -espaces vectoriels et soit
-espaces vectoriels et soit ![]() une application linéaire.
une application linéaire.
On considère une famille ![]() de vecteurs de
de vecteurs de ![]()
On note ![]()
Montrer que :
- si
 est injective et si
est injective et si 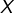 est libre, alors
est libre, alors 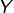 est libre.
est libre. - si
 est surjective et
est surjective et 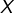 est génératrice de
est génératrice de 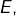 alors
alors 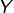 est génératrice de
est génératrice de 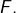

Soit ![]() un polynôme de degré
un polynôme de degré ![]() et soient
et soient ![]() des réels tous distincts.
des réels tous distincts.
Montrer que la famille ![]() est une base de
est une base de ![]()

Soit ![]() un
un ![]() -ev de dimension
-ev de dimension ![]() et soient
et soient ![]() des formes linéaires sur
des formes linéaires sur ![]()
Montrer l’équivalence des assertions :
 est libre
est libre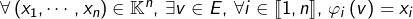

On considère un ![]() -espace vectoriel normé
-espace vectoriel normé ![]() .
.
Soient ![]() et
et ![]() deux suites convergentes à termes dans
deux suites convergentes à termes dans ![]()
Leurs limites respectives sont notées ![]() et
et ![]()
Montrer que si la famille ![]() est liée pour tout
est liée pour tout ![]() alors la famille
alors la famille ![]() est aussi liée.
est aussi liée.
La réciproque est-elle vraie ?
Cliquer ici pour accéder aux indications
Cliquer ici pour accéder aux solutions


Bonjour, comment allez-vous ? Que Dieu vous bénisse à jamais.
Merci Salif 🙂