Neuf énoncés d’exercices sur la dérivation des fonctions – 02

L’application ![]() est-elle dérivable en
est-elle dérivable en ![]() ?
?
Quel peut bien être l’intérêt de cet exercice ?

Trouver, pour tout ![]() une expression plus simple pour :
une expression plus simple pour :
![]()

Soit ![]() dérivable. On suppose que
dérivable. On suppose que ![]() est impaire. Que peut-on dire de
est impaire. Que peut-on dire de ![]() ?
?
Même question en supposant plutôt que ![]() est paire.
est paire.

Soit ![]() dérivable. Pour tout
dérivable. Pour tout ![]() on note
on note ![]() la
la ![]() ème itérée de
ème itérée de ![]() On rappelle que, par définition :
On rappelle que, par définition :
![]()
- On suppose que
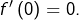 Calculer
Calculer 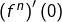 pour tout
pour tout 
- Même question en supposant que
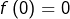 et
et 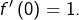

On considère l’application ![]()
Calculer ![]() pour tout
pour tout ![]()

On pose, pour tout ![]() :
:
![]()
Préciser les valeurs de ![]() et de
et de ![]()

On pose, pour tout ![]() :
:
![]()

Soit ![]() de classe
de classe ![]() On suppose qu’il existe un polynôme
On suppose qu’il existe un polynôme ![]() de degré impair tel que :
de degré impair tel que :
![]()

Soit ![]() de classe
de classe ![]() et bornée. On suppose que
et bornée. On suppose que ![]() s’annule au moins
s’annule au moins ![]() fois (pour un certain entier
fois (pour un certain entier ![]() et l’on considère un réel
et l’on considère un réel ![]() Montrer que l’application
Montrer que l’application ![]() définie par :
définie par :
![]()
Cliquer ici pour accéder aux indications
Cliquer ici pour accéder aux solutions

