
En utilisant des sommes de Riemann, calculer ![]() ainsi que
ainsi que ![]()

Calculer 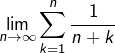

Calculer ![Rendered by QuickLaTeX.com \displaystyle{\lim_{n\rightarrow\infty}\left[\prod_{k=1}^{n}\left(1+\frac{k^{2}}{n^{2}}\right)\right]^{1/n}}](https://math-os.com/wp-content/ql-cache/quicklatex.com-5f07f31f71b0a2627d81b8f812b47cf8_l3.png)

Trouver un équivalent, lorsque ![]() de
de 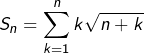

Le théorème de convergence des sommes de Riemann a été démontré ici, pour une application ![]() supposée continue.
supposée continue.
Simplifier (un peu) cette preuve dans le cas où ![]() est supposée lipschitzienne.
est supposée lipschitzienne.

Soit ![]() une application continue. Calculer
une application continue. Calculer 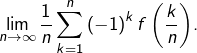

Soit ![]() bijective, strictement croissante et de classe
bijective, strictement croissante et de classe ![]() Calculer :
Calculer :
![]()

Soit ![]() continue, croissante et intégrable. Montrer que :
continue, croissante et intégrable. Montrer que :
![Rendered by QuickLaTeX.com \[ \lim_{n\rightarrow\infty}\,\frac{1}{n}\sum_{k=0}^{n-1}\,f\left(\frac{k}{n}\right)=\int_{0}^{1}f\left(x\right)\thinspace dx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a21fd636e130ce536d386c32c1b1d65a_l3.png)
En déduire le calcul de ![]() après avoir justifié la convergence de cette intégrale impropre.
après avoir justifié la convergence de cette intégrale impropre.

L’espace ![]() est muni de la norme
est muni de la norme ![]()
Pour tout ![]() on définit l’application
on définit l’application ![]() par :
par :
![]()
Montrer que si ![]() vérifie
vérifie ![]() alors
alors ![]() est constante.
est constante.
Cliquer ici pour accéder aux indications
Cliquer ici pour accéder aux solutions

