Solutions détaillées de neuf exercices sur les sommes de Riemann.
Cliquer ici pour accéder aux énoncés.
Posons :
![Rendered by QuickLaTeX.com \[ A=\int_{0}^{1}t^{2}\thinspace dt\qquad\text{et}\qquad B=\int_{0}^{1}e^{t}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-eb8d7c9e741e8992fc17ff94547f0c89_l3.png)
D’une part, 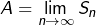 avec :
avec :
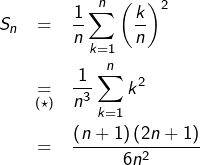
Or 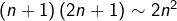 lorsque
lorsque 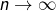 et donc :
et donc :
![Rendered by QuickLaTeX.com \[\boxed{A=\frac{1}{3}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1a281bed2f9bcb7c44a497317b404173_l3.png)
Pour l’égalité 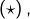 on pourra consulter cette vidéo ou du moins ce passage.
on pourra consulter cette vidéo ou du moins ce passage.
D’autre part, 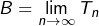 avec :
avec :
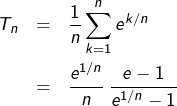
Or, on sait que 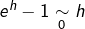 et donc :
et donc :
![Rendered by QuickLaTeX.com \[\boxed{B=e-1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6f50da43a4c5d1966f3e0ce8081f9c48_l3.png)
Pour rester dans l’esprit de cette fiche d’exercices, observons que pour tout 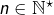 :
:
![Rendered by QuickLaTeX.com \[ \sum_{k=1}^{n}\frac{1}{n+k}=\frac{1}{n}\sum_{k=1}^{n}\frac{1}{1+\frac{k}{n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6af164e8d69d63be7b6309d98f2325ba_l3.png)
On reconnaît ainsi une somme de Riemann attachée à ![Rendered by QuickLaTeX.com f:\left[0,1\right]\rightarrow\mathbb{R},\thinspace t\mapsto\frac{1}{1+t}.](https://math-os.com/wp-content/ql-cache/quicklatex.com-4c172c97cfa857aa01d0cef5a82fe48b_l3.png)
Or :
![Rendered by QuickLaTeX.com \[ \int_{0}^{1}\frac{dt}{1+t}=\left[\ln\left(1+t\right)\right]_{0}^{1}=\ln\left(2\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7065f786c229e6c3d64e7a3f63c9db39_l3.png)
Et par conséquent :
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow\infty}\sum_{k=1}^{n}\frac{1}{n+k}=\ln\left(2\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9dbe4d5d39b6ac57c0c75f63e2856012_l3.png)
Voici à présent un autre point de vue.
On note, pour tout 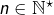 :
:
![Rendered by QuickLaTeX.com \[ H_{n}=\sum_{k=1}^{n}\frac{1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ccd178f4728a35226633816b17fa2881_l3.png)
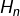 est le
est le 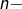 ème nombre harmonique.
ème nombre harmonique.
Il est classique (voir par exemple ici) que la suite de terme général :
![Rendered by QuickLaTeX.com \[ x_{n}=H_{n}-\ln\left(n\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-47f5de19c392bf9d2a3287878415d079_l3.png)
est convergente. Sa limite, appelée « constante d’Euler », est traditionnellement notée
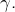
On observe que :
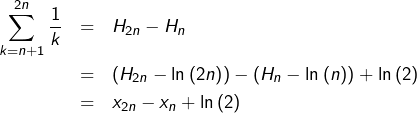
ce qui permet de retrouver la formule encadrée.
Posons ![Rendered by QuickLaTeX.com {\displaystyle u_{n}=\left[\prod_{k=1}^{n}\left(1+\frac{k^{2}}{n^{2}}\right)\right]^{1/n}}.](https://math-os.com/wp-content/ql-cache/quicklatex.com-efb5be82a569684daac2c2696f10f065_l3.png)
En passant au logarithme, on reconnaît une somme de Riemann :
![Rendered by QuickLaTeX.com \[ \ln\left(u_{n}\right)=\frac{1}{n}\sum_{k=1}^{n}\ln\left(1+\frac{k^{2}}{n^{2}}\right)\underset{n\rightarrow\infty}{\longrightarrow}\int_{0}^{1}\ln\left(1+t^{2}\right)\,dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fb34fe535ff349895faa592c7fcfa15a_l3.png)
En intégrant par parties, on obtient :
![Rendered by QuickLaTeX.com \begin{eqnarray*}\int_{0}^{1}\ln\left(1+t^{2}\right)\,dt & = & \left[t\ln\left(1+t^{2}\right)\right]_{0}^{1}-\int_{0}^{1}\frac{2t^{2}}{1+t^{2}}dt\\& = & \ln\left(2\right)-2\int_{0}^{1}\left(1-\frac{1}{1+t^{2}}\right)\,dt\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-609bb3b5d304190c7116a49213d66c2f_l3.png)
Or :
![Rendered by QuickLaTeX.com \[ \int_{0}^{1}\frac{dt}{1+t^{2}}=\left[\arctan\left(t\right)\right]_{0}^{1}=\frac{\pi}{4}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2cd385a922a8ceeb141e58d3725db3cb_l3.png)
Ainsi :
![Rendered by QuickLaTeX.com \[\int_{0}^{1}\ln\left(1+t^{2}\right)\,dt=\ln\left(2\right)-2+\frac{\pi}{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3e700d1792cb26c5bf5e24d5fe606956_l3.png)
et finalement :
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow\infty}u_{n}=2\,e^{\frac{\pi}{2}-2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f95daaae4429468dc47fc501c36ac3c4_l3.png)
Pour une version plus élaborée de la même question, voir l’exercice n° 8 de cette fiche.
On constate que, pour tout 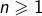 :
:
![Rendered by QuickLaTeX.com \[\frac{S_{n}}{n^{5/2}}=\frac{1}{n}\sum_{k=1}^{n}\frac{k}{n}\sqrt{1+\frac{k}{n}}\underset{n\rightarrow\infty}{\rightarrow}\int_{0}^{1}t\sqrt{1+t}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8da15dbaaf10f2bca8dba13c9aed2501_l3.png)
Or, en posant 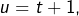 il vient :
il vient :
![Rendered by QuickLaTeX.com \begin{eqnarray*}\int_{0}^{1}t\sqrt{1+t}\thinspace dt & = & \int_{1}^{2}\left(u-1\right)\sqrt{u}\thinspace du\\& = & \left[\frac{2}{5}u^{5/2}-\frac{2}{3}u^{3/2}\right]_{1}^{2}\\& = & \frac{8\sqrt{2}}{5}-\frac{4\sqrt{2}}{3}-\frac{2}{5}+\frac{2}{3}\\& = & \frac{4\left(\sqrt{2}+1\right)}{15}\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-d2b9127b90b8a448a4e97bc228262f13_l3.png)
Ainsi :
![Rendered by QuickLaTeX.com \[ \boxed{S_{n}\sim\frac{4\left(\sqrt{2}+1\right)n^{5/2}}{15}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5c282fa68481a6ca9afba736d4aea996_l3.png)
Soit ![Rendered by QuickLaTeX.com f:\left[0,1\right]\rightarrow\mathbb{R}](https://math-os.com/wp-content/ql-cache/quicklatex.com-24d21c2af9c99ccd14b07bf411b8970d_l3.png) une application
une application 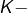 lipschitzienne (avec
lipschitzienne (avec 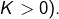
Notons, pour tout 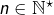 :
:
![Rendered by QuickLaTeX.com \[ S_{n}=\frac{1}{n}\sum_{k=1}^{n}f\left(\frac{k}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-72123a2f0a57ab9d1f4c6d8213acf995_l3.png)
![Rendered by QuickLaTeX.com \[ \Delta_{n}=\int_{0}^{1}f\left(x\right)\thinspace dx-S_{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fa35e5a260fa4b747380583950df9634_l3.png)
et montrons que
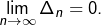
D’après la relation de Chasles :
![Rendered by QuickLaTeX.com \[\int_{0}^{1}f\left(x\right)\thinspace dx = \sum_{k=1}^{n}\int_{\left(k-1\right)/n}^{k/n}f\left(x\right)\thinspace dx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-596d097a04bd9a9be1512348bc660586_l3.png)
et donc :
![Rendered by QuickLaTeX.com \[ \Delta_{n}=\sum_{k=1}^{n}\int_{\left(k-1\right)/n}^{k/n}\left(f\left(x\right)-f\left(\frac{k}{n}\right)\right)\thinspace dx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bcbdef012e794c5bd65126b536ba80ed_l3.png)
puis, d’après l’inégalité triangulaire :
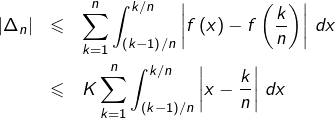
Or, pour tout 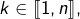 on voit en posant
on voit en posant 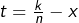 :
:
![Rendered by QuickLaTeX.com \[ \int_{\left(k-1\right)/n}^{k/n}\left|x-\frac{k}{n}\right|\thinspace dx=\int_{0}^{1/n}t\thinspace dt=\frac{1}{2n^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-21e6d17aaa9f24d5d31d79378b1e6cdd_l3.png)
Ainsi :
![Rendered by QuickLaTeX.com \[\boxed{\left|\Delta_{n}\right|\leqslant\frac{K}{2n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3bcad6998531a50a765512035bd0d62e_l3.png)
d’où le résultat annoncé.
Posons, pour tout 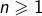 :
:
![Rendered by QuickLaTeX.com \[ A_{n}=\sum_{k=1}^{n}\left(-1\right)^{k}f\left(\frac{k}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c5fd32483e4215727ba02ddb605718ba_l3.png)
Intuitivement, lorsque  est grand, deux termes consécutifs de cette somme ont des valeurs absolues très voisines et (le plus souvent) des signes contraires. Ceci laisse penser que :
est grand, deux termes consécutifs de cette somme ont des valeurs absolues très voisines et (le plus souvent) des signes contraires. Ceci laisse penser que :
![Rendered by QuickLaTeX.com \[ \lim_{n\rightarrow\infty}\frac{A_{n}}{n}=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-48315c1e434d18f5d8b8768ef95af7d4_l3.png)
ce qu’on va maintenant établir rigoureusement.
Pour cela, groupons les termes deux par deux (les deux premiers, les deux suivants, etc … avec un éventuel terme isolé en fin de somme, si  est impair).
est impair).
On obtient ainsi :
![Rendered by QuickLaTeX.com \[ A_{n}=\sum_{p=1}^{\left\lfloor n/2\right\rfloor }\left(f\left(\frac{2p}{n}\right)-f\left(\frac{2p-1}{n}\right)\right)+\theta_{n}\,f\left(1\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6a30ddeb7050d041dc77d924841a92a0_l3.png)
avec :
![Rendered by QuickLaTeX.com \[ \theta_{n}=\begin{cases} 0 & \mbox{si }n\mbox{ pair}\\ -1 & \mbox{sinon} \end{cases}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1cbf9bff044ea3ed187473d4d6ba0f67_l3.png)
et donc, (inégalité triangulaire) :
![Rendered by QuickLaTeX.com \[ \left|A_{n}\right|\leqslant\sum_{p=1}^{\left\lfloor n/2\right\rfloor }\left|f\left(\frac{2p}{n}\right)-f\left(\frac{2p-1}{n}\right)\right|+\left\Vert f\right\Vert_{\infty}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3e3dc166cd00fbf0eab2b336bfda2161_l3.png)
Etant donné 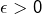 et vu que
et vu que  est uniformément continue (d’après le théorème de Heine), il existe
est uniformément continue (d’après le théorème de Heine), il existe 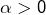 tel que :
tel que :
![Rendered by QuickLaTeX.com \[\forall\left(x,x'\right)\in\left[0,1\right]^{2},\,\left|x-x'\right|\leqslant\alpha\Rightarrow\left|f\left(x\right)-f\left(x'\right)\right|\leqslant\epsilon\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ad53fab7593d429632ea56ac35df05ff_l3.png)
Donc, dès que 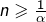 :
:
![Rendered by QuickLaTeX.com \[\left|A_{n}\right|\leqslant\epsilon\left\lfloor \frac{n}{2}\right\rfloor +\left\Vert f\right\Vert_{\infty}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-64b312e8de5af04316fb7245444c424a_l3.png)
puis :
![Rendered by QuickLaTeX.com \[\left|\frac{A_{n}}{n}\right|\leqslant\frac{\epsilon}{2}+\frac{1}{n}\left\Vert f\right\Vert_{\infty}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1f80309b9eb0f2b4f7e046c7c468c78e_l3.png)
Ainsi :
![Rendered by QuickLaTeX.com \[n\geqslant\max\left\{\frac{1}{\alpha},\frac{2}{\epsilon}\left\Vert f\right\Vert_{\infty}\right\} \Rightarrow\left|\frac{A_{n}}{n}\right|\leqslant\epsilon\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-dc10e262d0b7089eca537bdcb8a8fbe2_l3.png)
On a montré que :
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow\infty}\frac{1}{n}\sum_{k=1}^{n}\left(-1\right)^{k}f\left(\frac{k}{n}\right)=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2185353ca823929aa7bedeb95c6de752_l3.png)
Transformons l’intégrale 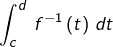 en posant
en posant 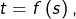 ce qui est licite puisque
ce qui est licite puisque  est supposée de classe
est supposée de classe 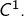 On obtient :
On obtient :
![Rendered by QuickLaTeX.com \[ \int_{c}^{d}\,f^{-1}\left(t\right)\,dt=\int_{a}^{b}\,s\,f'\left(s\right)\,ds\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fb29e781c69f03966809e5f2eaa26664_l3.png)
Une intégration par parties donne ensuite :
![Rendered by QuickLaTeX.com \[ \int_{a}^{b}\,s\,f'\left(s\right)\,ds=\left[s\thinspace f\left(s\right)\right]_{a}^{b}-\int{a}^{b}f\left(s\right)\thinspace ds\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b01cd835b64b763ffadcb2cf5aa40740_l3.png)
et donc :
![Rendered by QuickLaTeX.com \[ \int_{a}^{b}\,f\left(t\right)\,dt+\int_{c}^{d}\,f^{-1}\left(t\right)\,dt=b\,f\left(b\right)-a\,f\left(a\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7a3c14195b9521e35680538d3d21cabe_l3.png)
c’est-à-dire :
![Rendered by QuickLaTeX.com \[\boxed{\int_{a}^{b}\,f\left(t\right)\,dt+\int_{c}^{d}\,f^{-1}\left(t\right)\,dt=bd-ac}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0e5abe8d975d99f40c76a9690fc35d9b_l3.png)
Affaiblissons maintenant l’hypothèse en supposant  seulement continue.
seulement continue.
Pour 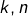 entiers tels que
entiers tels que 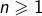 et
et 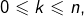 posons :
posons :
![Rendered by QuickLaTeX.com \[ x_{k,n}=a+\frac{k\left(b-a\right)}{n}\qquad\textrm{et}\qquad y_{k,n}=f\left(x_{k,n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-10eac00e781641c73525c79fccbc8434_l3.png)
Ainsi que :
![Rendered by QuickLaTeX.com \[ S_{n}=\frac{b-a}{n}\,\sum_{k=0}^{n-1}\,f\left(x_{k,n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5ff5cdc3a672e4d94690a082f6d14daa_l3.png)
et
![Rendered by QuickLaTeX.com \[ T_{n}=\sum_{k=0}^{n-1}\,\left(y_{n,k+1}-y_{n,k}\right)x_{n,k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-edf1daf8f478b53be580eb9ac12026d4_l3.png)
On sait que :
![Rendered by QuickLaTeX.com \[ \lim_{n\rightarrow\infty}\,S_{n}=\int_{a}^{b}\,f\left(t\right)\,dt\qquad\left(\clubsuit\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3d79c3deb20bc7a050082b8e7c1f9615_l3.png)
Comme  est strictement croissante,
est strictement croissante, 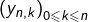 est une subdivision de
est une subdivision de ![Rendered by QuickLaTeX.com \left[c,d\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cb5e811ed0512e7d4bdf0b8c942ddcfe_l3.png) (c’est-à-dire : une liste strictement croissante dont le premier et le dernier terme sont respectivement
(c’est-à-dire : une liste strictement croissante dont le premier et le dernier terme sont respectivement  et
et 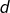 ).
).
En outre, comme  est uniformément continue, le pas de cette subdivision tend vers 0 :
est uniformément continue, le pas de cette subdivision tend vers 0 :
![Rendered by QuickLaTeX.com \[ \lim_{n\rightarrow\infty}\max\left\{y_{n,k+1}-y_{n,k};\,0\leqslant k\leqslant n-1\right\}=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-44c0880377af376e5805cc37bb06fceb_l3.png)
D’après le théorème de convergence des sommes de Riemann :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}\,T_{n}=\int_{c}^{d}\,f^{-1}\left(t\right)\,dt\qquad\left(\spadesuit\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f3fc2d008e0bb2915b1375ad9cb65ec5_l3.png)
Mais, pour tout 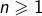 :
:
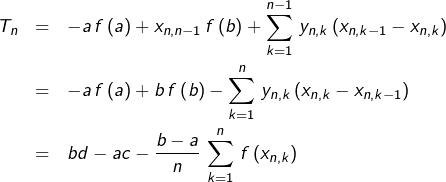
et donc :
![Rendered by QuickLaTeX.com \[ S_{n}+T_{n}=bd-ac+\frac{b-a}{n}\left(c-d\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ba9d2c41b9a433b5121a1a7cf0572c04_l3.png)
En passant à la limite dans cette dernière égalité, on retrouve la formule encadrée plus haut.
Soit 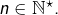 Comme
Comme  est croissante sur
est croissante sur 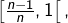 on a pour tout
on a pour tout 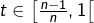 :
:
![Rendered by QuickLaTeX.com \[ \left(t-\frac{n-1}{n}\right)\,f\left(\frac{n-1}{n}\right)\leqslant\int_{\frac{n-1}{n}}^{t}\,f\left(x\right)\,dx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-36c9a690d494d62cce61520f338102d5_l3.png)
d’où en faisant 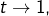 et compte tenu de la convergence de l’intégrale impropre
et compte tenu de la convergence de l’intégrale impropre 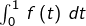 :
:
(1) 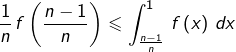
Pour 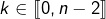 vue la croissance de
vue la croissance de  sur
sur ![Rendered by QuickLaTeX.com \left[\frac{k}{n},\,\frac{k+1}{n}\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c471520050b1fb542544972c0bb3f77d_l3.png) :
:
(2) 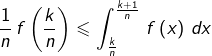
D’après (1) et (2), on obtient après sommation :
(3) 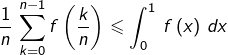
De même, pour tout 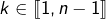 :
:
![Rendered by QuickLaTeX.com \[ \int_{\frac{k-1}{n}}^{\frac{k}{n}}\,f\left(x\right)\,dx\leqslant\frac{1}{n}\,f\left(\frac{k}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fc419fd7dad4961c91a2872393ec6d39_l3.png)
et par sommation :
(4) 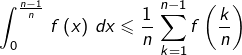
D’après (3) et (4) :
![Rendered by QuickLaTeX.com \[ \frac{f\left(0\right)}{n}+\int_{0}^{\frac{n-1}{n}}\,f\left(x\right)\,dx\leqslant\frac{1}{n}\,\sum_{k=0}^{n-1}f\left(\frac{k}{n}\right)\leqslant\int_{0}^{1}\,f\left(x\right)\,dx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7a891f6e78a3ac91ef09c91a60bfe2c9_l3.png)
ce qui prouve que :
![Rendered by QuickLaTeX.com \[ \boxed{\lim_{n\rightarrow+\infty}\,\frac{1}{n}\,\sum_{k=0}^{n-1}f\left(\frac{k}{n}\right)=\int_{0}^{1}\,f\left(x\right)\,dx}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fa7f17524581a2ef3038266855e87ec3_l3.png)
APPLICATION – L’application
![Rendered by QuickLaTeX.com \[f\,:\,\left]0,\pi\right[\rightarrow\mathbb{R},\,x\mapsto\ln\left(\sin\left(x\right)\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-98aec3c6df542fba815f5bcc7667acf4_l3.png)
est continue.

est croissante sur
![Rendered by QuickLaTeX.com \left]0,\frac{\pi}{2}\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7551e859aa107fd9f7a350e68560b624_l3.png)
et l’intégrale impropre
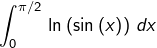 converge
converge.
Détail (cliquer pour déplier / replier)
La fonction 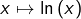 est intégrable sur
est intégrable sur ![Rendered by QuickLaTeX.com \left]0,\frac{\pi}{2}\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7551e859aa107fd9f7a350e68560b624_l3.png) et de signe constant (négatif). Or :
et de signe constant (négatif). Or :
![Rendered by QuickLaTeX.com \[\ln\left(\sin\left(x\right)\right)\underset{{\scriptstyle 0}}{\sim}\ln\left(x\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-efe4f49371c4e20480d2dad6dfa32152_l3.png)
donc, d’après la règle des équivalents,
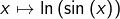
est intégrable sur
![Rendered by QuickLaTeX.com \left]0,\frac{\pi}{2}\right].](https://math-os.com/wp-content/ql-cache/quicklatex.com-d2e89815b45bb5c4919d6c80e42a3a76_l3.png)
 décroissante sur
décroissante sur 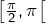 et l’intégrale impropre
et l’intégrale impropre 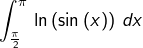 converge aussi (poser
converge aussi (poser 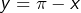 pour se ramener à l’intégrale précédente).
pour se ramener à l’intégrale précédente).
En adaptant légèrement le résultat démontré plus haut ( n’est pas monotone, mais ses restrictions aux intervalles
n’est pas monotone, mais ses restrictions aux intervalles ![Rendered by QuickLaTeX.com \left]0,\frac\pi2\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7dc19b783881390620c7c86d3ca1d306_l3.png) et
et 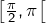 le sont), on obtient :
le sont), on obtient :
![Rendered by QuickLaTeX.com \[ \int_{0}^{\pi}\,\ln\left(\sin\left(x\right)\right)\,dx=\lim_{n\rightarrow+\infty}\,T_{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4639bb145205a8cacf7623a38637ee17_l3.png)
où l’on a posé :
![Rendered by QuickLaTeX.com \[T_{n}=\frac{\pi}{n}\,\sum_{k=1}^{n-1}\,\ln\left(\sin\left(\frac{k\pi}{n}\right)\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7bd6ab1778a99cb7dca635fe2b74e517_l3.png)
Or, un calcul classique (voir l’exercice 9 de cette fiche) montre que :
![Rendered by QuickLaTeX.com \[\prod_{k=1}^{n-1}\,\sin\left(\frac{k\pi}{n}\right)=\frac{n}{2^{n-1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-be71c0e50d0e9873d949581920ba11bf_l3.png)
et donc
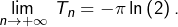
Finalement :
![Rendered by QuickLaTeX.com \[\boxed{\int_{0}^{\pi/2}\,\ln\left(\sin\left(x\right)\right)\,dx=-\frac{\pi}{2}\ln\left(2\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-93f1302ce3b0a94a5f89056c0d3beef8_l3.png)
Remarque
On pourra retrouver ces calculs dans cette vidéo :
Soit 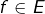 telle que
telle que 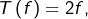 c’est-à-dire :
c’est-à-dire :
![Rendered by QuickLaTeX.com \[ \forall x\in\left[0,1\right],\,f\left(x\right)=\frac{1}{2}\left[f\left(\frac{x}{2}\right)+f\left(\frac{x+1}{2}\right)\right]\qquad\left(\star\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a7c2bfa0dfe5a53c1b6b767703d330f1_l3.png)
On déduit de 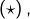 en raisonnant par récurrence que, pour tout
en raisonnant par récurrence que, pour tout 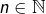 et pour tout
et pour tout ![Rendered by QuickLaTeX.com x\in\left[0,1\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-07b514b1e0c7996db17eecb846a1a881_l3.png) :
:
![Rendered by QuickLaTeX.com \[ f\left(x\right)=\frac{1}{2^{n}}\,\sum_{k=0}^{2^{n}-1}\,f\left(\frac{x+k}{2^{n}}\right)\qquad\left(\star\star\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-caefcf17c9e41991db38c7e16da34ca9_l3.png)
Notons 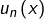 le second membre de cette égalité et posons :
le second membre de cette égalité et posons :
![Rendered by QuickLaTeX.com \[ S_{n}=\frac{1}{2^{n}}\,\sum_{k=0}^{2^{n}-1}\,f\left(\frac{k}{2^{n}}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e2f03789ca84cd1d4da7c7fbb205038c_l3.png)
On reconnaît une somme de Riemann attachée à  et l’on sait que :
et l’on sait que :
![Rendered by QuickLaTeX.com \[ \lim_{n\rightarrow\infty}\,S_{n}=\int_{0}^{1}\,f\left(t\right)\,dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-506baada11785f78130af1e57fed2c83_l3.png)
Par ailleurs, d’après le théorème de Heine,  est uniformément continue.
est uniformément continue.
Etant donné 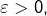 il existe donc
il existe donc 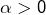 tel que :
tel que :
![Rendered by QuickLaTeX.com \[ \forall\left(x,x'\right)\in\left[0,1\right]^{2},\,\left|x'-x\right|\leqslant\alpha\Rightarrow\left|f\left(x'\right)-f\left(x\right)\right|\leqslant\varepsilon\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a6c8de4b054131d8f2decbcfbe9ce0dd_l3.png)
Ainsi, dès que 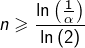 :
:
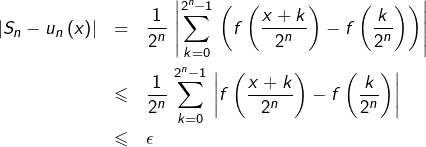
et donc :
![Rendered by QuickLaTeX.com \[ \lim_{n\rightarrow\infty}\,u_{n}\left(x\right)=\int_{0}^{1}\,f\left(t\right)\,dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b8a10973dd4d25281349b3a6a4a9e279_l3.png)
En passant à la limite dans 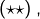 on obtient donc :
on obtient donc :
![Rendered by QuickLaTeX.com \[\boxed{\forall x\in\left[0,1\right],\,f\left(x\right)=\int_{0}^{1}\,f\left(t\right)\,dt}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b752fabbdffdb8e2c9e0660c0f136cef_l3.png)
Bref,  est constante.
est constante.
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
![]()
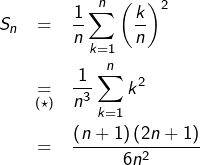
![Rendered by QuickLaTeX.com \[\boxed{A=\frac{1}{3}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1a281bed2f9bcb7c44a497317b404173_l3.png)
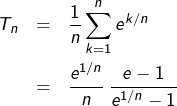
![]()
![Rendered by QuickLaTeX.com \[ \sum_{k=1}^{n}\frac{1}{n+k}=\frac{1}{n}\sum_{k=1}^{n}\frac{1}{1+\frac{k}{n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6af164e8d69d63be7b6309d98f2325ba_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow\infty}\sum_{k=1}^{n}\frac{1}{n+k}=\ln\left(2\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9dbe4d5d39b6ac57c0c75f63e2856012_l3.png)
![Rendered by QuickLaTeX.com \[ H_{n}=\sum_{k=1}^{n}\frac{1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ccd178f4728a35226633816b17fa2881_l3.png)
![]()
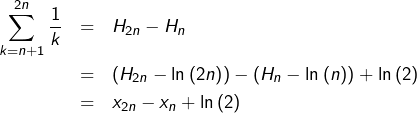
![Rendered by QuickLaTeX.com \[ \ln\left(u_{n}\right)=\frac{1}{n}\sum_{k=1}^{n}\ln\left(1+\frac{k^{2}}{n^{2}}\right)\underset{n\rightarrow\infty}{\longrightarrow}\int_{0}^{1}\ln\left(1+t^{2}\right)\,dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fb34fe535ff349895faa592c7fcfa15a_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*}\int_{0}^{1}\ln\left(1+t^{2}\right)\,dt & = & \left[t\ln\left(1+t^{2}\right)\right]_{0}^{1}-\int_{0}^{1}\frac{2t^{2}}{1+t^{2}}dt\\& = & \ln\left(2\right)-2\int_{0}^{1}\left(1-\frac{1}{1+t^{2}}\right)\,dt\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-609bb3b5d304190c7116a49213d66c2f_l3.png)
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\frac{S_{n}}{n^{5/2}}=\frac{1}{n}\sum_{k=1}^{n}\frac{k}{n}\sqrt{1+\frac{k}{n}}\underset{n\rightarrow\infty}{\rightarrow}\int_{0}^{1}t\sqrt{1+t}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8da15dbaaf10f2bca8dba13c9aed2501_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*}\int_{0}^{1}t\sqrt{1+t}\thinspace dt & = & \int_{1}^{2}\left(u-1\right)\sqrt{u}\thinspace du\\& = & \left[\frac{2}{5}u^{5/2}-\frac{2}{3}u^{3/2}\right]_{1}^{2}\\& = & \frac{8\sqrt{2}}{5}-\frac{4\sqrt{2}}{3}-\frac{2}{5}+\frac{2}{3}\\& = & \frac{4\left(\sqrt{2}+1\right)}{15}\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-d2b9127b90b8a448a4e97bc228262f13_l3.png)
![Rendered by QuickLaTeX.com \[ \boxed{S_{n}\sim\frac{4\left(\sqrt{2}+1\right)n^{5/2}}{15}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5c282fa68481a6ca9afba736d4aea996_l3.png)
![Rendered by QuickLaTeX.com \[ S_{n}=\frac{1}{n}\sum_{k=1}^{n}f\left(\frac{k}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-72123a2f0a57ab9d1f4c6d8213acf995_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\int_{0}^{1}f\left(x\right)\thinspace dx = \sum_{k=1}^{n}\int_{\left(k-1\right)/n}^{k/n}f\left(x\right)\thinspace dx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-596d097a04bd9a9be1512348bc660586_l3.png)
![Rendered by QuickLaTeX.com \[ \Delta_{n}=\sum_{k=1}^{n}\int_{\left(k-1\right)/n}^{k/n}\left(f\left(x\right)-f\left(\frac{k}{n}\right)\right)\thinspace dx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bcbdef012e794c5bd65126b536ba80ed_l3.png)
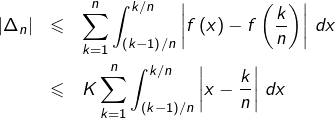
![Rendered by QuickLaTeX.com \[ \int_{\left(k-1\right)/n}^{k/n}\left|x-\frac{k}{n}\right|\thinspace dx=\int_{0}^{1/n}t\thinspace dt=\frac{1}{2n^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-21e6d17aaa9f24d5d31d79378b1e6cdd_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\left|\Delta_{n}\right|\leqslant\frac{K}{2n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3bcad6998531a50a765512035bd0d62e_l3.png)
![Rendered by QuickLaTeX.com \[ A_{n}=\sum_{k=1}^{n}\left(-1\right)^{k}f\left(\frac{k}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c5fd32483e4215727ba02ddb605718ba_l3.png)
![]()
![Rendered by QuickLaTeX.com \[ A_{n}=\sum_{p=1}^{\left\lfloor n/2\right\rfloor }\left(f\left(\frac{2p}{n}\right)-f\left(\frac{2p-1}{n}\right)\right)+\theta_{n}\,f\left(1\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6a30ddeb7050d041dc77d924841a92a0_l3.png)
![Rendered by QuickLaTeX.com \[ \theta_{n}=\begin{cases} 0 & \mbox{si }n\mbox{ pair}\\ -1 & \mbox{sinon} \end{cases}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1cbf9bff044ea3ed187473d4d6ba0f67_l3.png)
![Rendered by QuickLaTeX.com \[ \left|A_{n}\right|\leqslant\sum_{p=1}^{\left\lfloor n/2\right\rfloor }\left|f\left(\frac{2p}{n}\right)-f\left(\frac{2p-1}{n}\right)\right|+\left\Vert f\right\Vert_{\infty}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3e3dc166cd00fbf0eab2b336bfda2161_l3.png)
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow\infty}\frac{1}{n}\sum_{k=1}^{n}\left(-1\right)^{k}f\left(\frac{k}{n}\right)=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2185353ca823929aa7bedeb95c6de752_l3.png)
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{\int_{a}^{b}\,f\left(t\right)\,dt+\int_{c}^{d}\,f^{-1}\left(t\right)\,dt=bd-ac}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0e5abe8d975d99f40c76a9690fc35d9b_l3.png)
![]() seulement continue.
seulement continue.![]()
![Rendered by QuickLaTeX.com \[ S_{n}=\frac{b-a}{n}\,\sum_{k=0}^{n-1}\,f\left(x_{k,n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5ff5cdc3a672e4d94690a082f6d14daa_l3.png)
![Rendered by QuickLaTeX.com \[ T_{n}=\sum_{k=0}^{n-1}\,\left(y_{n,k+1}-y_{n,k}\right)x_{n,k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-edf1daf8f478b53be580eb9ac12026d4_l3.png)
![]()
![]()
![]()
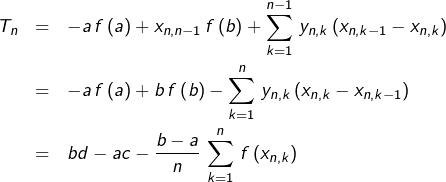
![]()
![Rendered by QuickLaTeX.com \[ \left(t-\frac{n-1}{n}\right)\,f\left(\frac{n-1}{n}\right)\leqslant\int_{\frac{n-1}{n}}^{t}\,f\left(x\right)\,dx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-36c9a690d494d62cce61520f338102d5_l3.png)
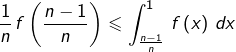
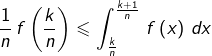
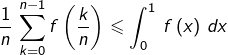
![Rendered by QuickLaTeX.com \[ \int_{\frac{k-1}{n}}^{\frac{k}{n}}\,f\left(x\right)\,dx\leqslant\frac{1}{n}\,f\left(\frac{k}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fc419fd7dad4961c91a2872393ec6d39_l3.png)
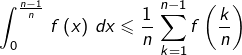
![Rendered by QuickLaTeX.com \[ \frac{f\left(0\right)}{n}+\int_{0}^{\frac{n-1}{n}}\,f\left(x\right)\,dx\leqslant\frac{1}{n}\,\sum_{k=0}^{n-1}f\left(\frac{k}{n}\right)\leqslant\int_{0}^{1}\,f\left(x\right)\,dx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7a891f6e78a3ac91ef09c91a60bfe2c9_l3.png)
![Rendered by QuickLaTeX.com \[ \boxed{\lim_{n\rightarrow+\infty}\,\frac{1}{n}\,\sum_{k=0}^{n-1}f\left(\frac{k}{n}\right)=\int_{0}^{1}\,f\left(x\right)\,dx}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fa7f17524581a2ef3038266855e87ec3_l3.png)
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[T_{n}=\frac{\pi}{n}\,\sum_{k=1}^{n-1}\,\ln\left(\sin\left(\frac{k\pi}{n}\right)\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7bd6ab1778a99cb7dca635fe2b74e517_l3.png)
![Rendered by QuickLaTeX.com \[\prod_{k=1}^{n-1}\,\sin\left(\frac{k\pi}{n}\right)=\frac{n}{2^{n-1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-be71c0e50d0e9873d949581920ba11bf_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\int_{0}^{\pi/2}\,\ln\left(\sin\left(x\right)\right)\,dx=-\frac{\pi}{2}\ln\left(2\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-93f1302ce3b0a94a5f89056c0d3beef8_l3.png)
![]()
![Rendered by QuickLaTeX.com \[ f\left(x\right)=\frac{1}{2^{n}}\,\sum_{k=0}^{2^{n}-1}\,f\left(\frac{x+k}{2^{n}}\right)\qquad\left(\star\star\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-caefcf17c9e41991db38c7e16da34ca9_l3.png)
![Rendered by QuickLaTeX.com \[ S_{n}=\frac{1}{2^{n}}\,\sum_{k=0}^{2^{n}-1}\,f\left(\frac{k}{2^{n}}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e2f03789ca84cd1d4da7c7fbb205038c_l3.png)
![]()
![]()
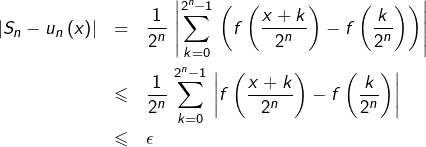
![]()
![Rendered by QuickLaTeX.com \[\boxed{\forall x\in\left[0,1\right],\,f\left(x\right)=\int_{0}^{1}\,f\left(t\right)\,dt}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b752fabbdffdb8e2c9e0660c0f136cef_l3.png)




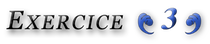
![Rendered by QuickLaTeX.com {\displaystyle u_{n}=\left[\prod_{k=1}^{n}\left(1+\frac{k^{2}}{n^{2}}\right)\right]^{1/n}}.](https://math-os.com/wp-content/ql-cache/quicklatex.com-efb5be82a569684daac2c2696f10f065_l3.png)