
Le calcul intégral apparaît (modestement) dans le programme de terminale scientifique.
L’objet de cet article est de présenter cette notion, en essayant de dégager l’idée géométrique sous-jacente, puis de détailler quelques exemples simples de calculs.
Le lien entre les points de vue géométrique (aire « sous la courbe ») et analytique (primitives) est abordé de façon non rigoureuse (mais intuitive) à la dernière section.
Si vous cherchez plutôt un texte « utilitaire », avec seulement quelques exemples de calculs, rendez-vous directement à la section 4 (mais je vous invite à revenir ultérieurement, pour lire l’article dans son ensemble).

Le moment venu, lorsque vous serez prêt(e), une fiche d’exercices entièrement corrigés vous attend !
1 – De quoi s’agit-il ?
Une intégrale se présente sous la forme :
![Rendered by QuickLaTeX.com \[\boxed{\int_{a}^{b}f\left(x\right)\thinspace dx}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-38c42a9db7a87444c5398ec65584f1e8_l3.png)
On peut prononcer ou non le « dx », c’est au choix… mais il faut le noter.
Dans cette écriture :
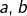 désignent des nombres réels; ce sont les bornes de l’intégrale,
désignent des nombres réels; ce sont les bornes de l’intégrale, désigne une fonction, supposée continue sur un intervalle contenant
désigne une fonction, supposée continue sur un intervalle contenant  et
et 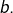
Si ![]() cette intégrale mesure l’aire (algébrique) du domaine limité par le graphe de
cette intégrale mesure l’aire (algébrique) du domaine limité par le graphe de ![]() l’axe des abscisses et les deux droites verticales d’équation
l’axe des abscisses et les deux droites verticales d’équation ![]() et
et ![]()
L’adjectif « algébrique » signifie que l’aire est comptée positivement si le graphe de ![]() est situé « au-dessus » de l’axe des abscisses et négativement dans le cas contraire.
est situé « au-dessus » de l’axe des abscisses et négativement dans le cas contraire.

Vers la fin du 17-ème siècle, à l’époque de Newton et Leibniz, on aurait dit que le symbole ![]() désigne une « variation infinitésimale de l’abscisse » et que l’aire du « rectangle infinitésimal » de côtés
désigne une « variation infinitésimale de l’abscisse » et que l’aire du « rectangle infinitésimal » de côtés ![]() et
et ![]() est égale au produit
est égale au produit ![]()
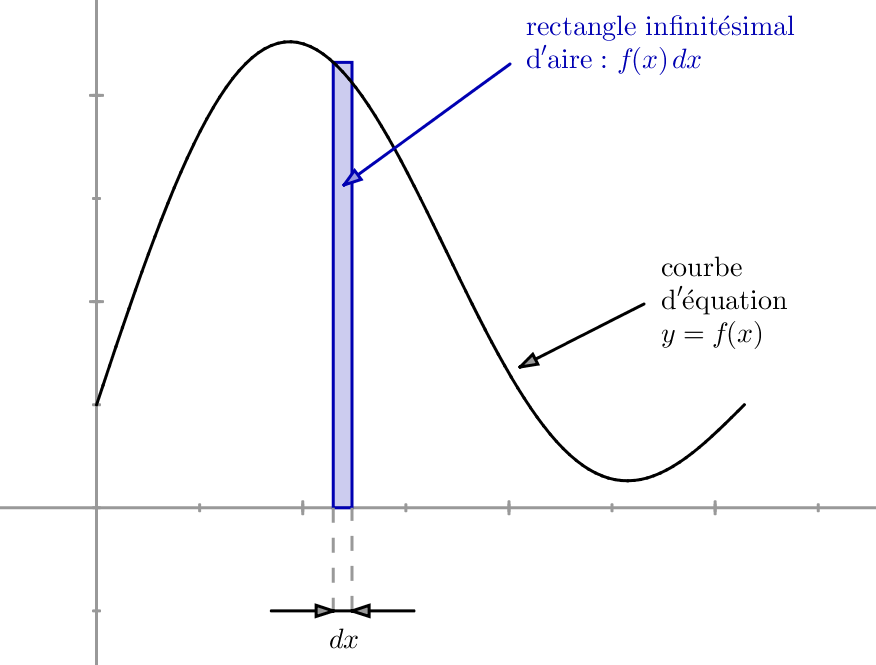
Quant au symbole ![]() c’est le vestige de la lettre S, initiale du mot somme.
c’est le vestige de la lettre S, initiale du mot somme.
En effet, l’idée de base était que :
L’aire du domaine limité par le graphe de ![]() l’axe des abscisses et les droites d’équations
l’axe des abscisses et les droites d’équations ![]() et
et ![]() est la « somme infinie » des aires de rectangles « infinitésimaux ».
est la « somme infinie » des aires de rectangles « infinitésimaux ».
L’illustration dynamique ci-dessous peut aider à comprendre cette idée. On y voit une collection de rectangles associés à une subdivision régulière de l’intervalle d’intégration.
Approximation d’une intégrale par une somme d’aires de rectangles
En déplaçant le curseur de la souris (ou du trackpad) latéralement au-dessus de l’image, on augmente ou l’on diminue le nombre n de « tranches ».
On note I la valeur exacte et A la somme des aires des rectangles.
Plus n est élevé, meilleure est l’approximation de l’intégrale par la somme (algébrique) des aires des rectangles. Autrement dit, l’écart ![]() tend vers 0 lorsque n tend vers l’infini.
tend vers 0 lorsque n tend vers l’infini.
Une présentation moderne (et rigoureuse) de ces idées repose sur les notions de borne supérieure et de limite. Cet article étant de niveau élémentaire, nous n’irons pas plus loin dans cette direction.
2 – Notion de primitive
Je présume que vous savez calculer la dérivée d’une fonction (pourvu qu’elle soit dérivable … et pas trop moche) : on enseigne cela dès la classe de première.
La primitivation est l’opération inverse :
On appelle primitive d’une fonction ![]() toute fonction dérivable
toute fonction dérivable ![]() dont la dérivée est
dont la dérivée est ![]()

Attention de bien dire une primitive (et non pas la primitive). En effet, en ajoutant une constante arbitraire à ![]() on trouve encore une primitive de
on trouve encore une primitive de ![]() De ce fait, si la fonction
De ce fait, si la fonction ![]() possède une primitive, alors elle en possède fatalement une infinité !
possède une primitive, alors elle en possède fatalement une infinité !
Exemple
La dérivée de ![]() est
est ![]()
Par conséquent, une primitive de ![]() est
est ![]() (et
(et ![]() en est une autre, tout comme
en est une autre, tout comme ![]()
Il est pratique de consigner les principales primitives connues dans un tableau à deux lignes : chaque colonne comporte deux fonctions, celle du bas étant une primitive de celle du haut.
Le tableau de primitives ci-dessous est modeste, mais c’est un bon début :
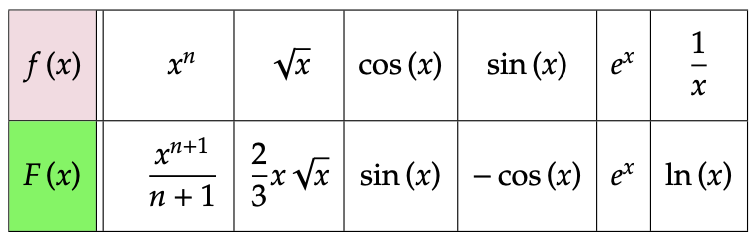
Dans la première colonne, l’entier ![]() est supposé positif ou nul. La formule reste valable pour un entier négatif, à condition qu’il soit différent de -1 et que l’intervalle de définition de la fonction ne contienne pas 0. Cette formule reste d’ailleurs valable pour une classe plus étendue d’exposants (la colonne 2 correspond au cas où
est supposé positif ou nul. La formule reste valable pour un entier négatif, à condition qu’il soit différent de -1 et que l’intervalle de définition de la fonction ne contienne pas 0. Cette formule reste d’ailleurs valable pour une classe plus étendue d’exposants (la colonne 2 correspond au cas où ![]() ). Pour aller plus loin, on pourra consulter cet article, où sont définies les fonctions puissances d’exposant quelconque.
). Pour aller plus loin, on pourra consulter cet article, où sont définies les fonctions puissances d’exposant quelconque.
3 – Petite digression pour les curieux
Ce qui précède peut sembler assez simple, mais il y a un hic …

Le calcul explicite des primitives d’une fonction n’est pas toujours faisable explicitement, à l’aide des fonctions dites « usuelles ».
On peut même dire qu’il est généralement infaisable …
Comprenons-nous bien : n’importe quelle fonction continue (sur un intervalle) possède des primitives (en terminale, on peut se contenter d’admettre ce théorème, car sa démonstration nécessite un bagage plus important). Mais on n’est pas sûr de savoir expliciter une telle primitive à l’aide des fonctions dites « usuelles » (polynômes, sinus et cosinus, exponentielle et logarithme, plus éventuellement quelques autres…) et de leurs composées.

Par exemple, on ne sait pas calculer explicitement de primitive pour la fonction ![]()
Vous doutez de cette affirmation ? Essayez… Vous verrez que vous ne parviendrez à rien.
A ce sujet, voici l’erreur classique du débutant :
ATTENTION : calcul FAUX !
On sait que la dérivée de ![]() est
est ![]()
Une primitive de ![]() est donc la fonction
est donc la fonction ![]()
Jusqu’ici, aucun doute possible.
Tentons maintenant une analogie…
En dérivant ![]() on trouve la fonction
on trouve la fonction ![]()
Par conséquent, la fonction ![]() serait une primitive de
serait une primitive de ![]()
Soyons prudents et vérifions …
On dérive ![]() en utilisant la formule de dérivation d’un quotient :
en utilisant la formule de dérivation d’un quotient :
![]()
![Rendered by QuickLaTeX.com \[F'\left(x\right)=\frac{\left(2xe^{x^{2}}\right)\left(2x\right)-2e^{x^{2}}}{4x^{2}}=\left(1-\frac{1}{2x^{2}}\right)e^{x^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-84f8bb506f5d619d0d664134b8556b5f_l3.png)
Manifestement, ça ne marche pas ! On ne retrouve pas ![]()
Mais alors, où est l’erreur ?
En fait, on a raisonné comme si le facteur ![]() était constant !
était constant !
Si ![]() est une primitive de
est une primitive de ![]() alors
alors ![]() est une primitive de
est une primitive de ![]() (
(![]() désigne une constante réelle). Mais si
désigne une constante réelle). Mais si ![]() est remplacé par
est remplacé par ![]() avec pour
avec pour ![]() une fonction dérivable, alors ce n’est plus la même chose. On doit utiliser la formule de dérivation d’un produit :
une fonction dérivable, alors ce n’est plus la même chose. On doit utiliser la formule de dérivation d’un produit :
![]()

Nous ne sommes pas parvenus à primitiver explicitement ![]()
Il y a une bonne raison à cela : on peut prouver l’impossibilité d’expliciter une telle fonction au moyen des fonctions usuelles… mais çà, c’est une autre paire de manches !!
Sans compter qu’il faudrait commencer par formuler avec précision ce que signifie cette impossibilité.
Fin de la digression, revenons à nos moutons…
4 – Exemples de calculs d’intégrales
Pour calculer l’intégrale ![]() il suffit de connaître une primitive
il suffit de connaître une primitive ![]() de
de ![]() de l’évaluer en
de l’évaluer en ![]() et en
et en ![]() puis de faire la différence.
puis de faire la différence.
Autrement dit :
![Rendered by QuickLaTeX.com \[\boxed{\int_{a}^{b}f\left(x\right)\thinspace dx=F\left(b\right)-F\left(a\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1edba11aa2474c1b54698fbd7ba641c9_l3.png)
Cette différence ![]() se note aussi
se note aussi ![]() On l’appelle la variation de
On l’appelle la variation de ![]() entre
entre ![]() et
et ![]() .
.
Pour expliquer proprement d’où provient l’égalité encadrée, encore faudrait-il avoir donné au préalable une vraie définition de la notion d’intégrale (ce qui n’a pas été fait ici). Néanmoins, en se fondant sur l’interprétation géométrique (aire du domaine « sous le graphe »), on peut tenter une justification (peu rigoureuse, mais c’est mieux que rien) : voir section 6, en fin d’article.
Détaillons cinq exemples simples.
Exemple 1
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{I_{1}=\int_{0}^{1}x^{2}\thinspace dx}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-eda12bcf59bdb6aaf2b51cd507db3235_l3.png)
On sait que la dérivée de ![]() est
est ![]()
On en déduit qu’une primitive de ![]() est
est ![]() Ainsi :
Ainsi :
![Rendered by QuickLaTeX.com \[I_{1}=\left[\frac{x^{3}}{3}\right]_{0}^{1}=\boxed{\frac{1}{3}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-85cbc32354bff8024c113bebda0b8f68_l3.png)
Exemple 2
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{I_{2}=\int_{1}^{2}\frac{1}{x^{2}}\thinspace dx}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-81d6cc5e8520cb64d5b56d61f118c510_l3.png)
On sait que la dérivée de ![]() est
est ![]() Une primitive de
Une primitive de ![]() est donc
est donc ![]()
On voit ainsi que :
![Rendered by QuickLaTeX.com \[I_{2}=\left[-\frac{1}{x}\right]_{1}^{2}=-\frac{1}{2}-\left(-1\right)=\boxed{\frac{1}{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2ec0816c3bd26b13df74bc2fb39fc1b4_l3.png)
Exemple 3
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{I_{3}=\int_{0}^{1}\frac{x}{1+x^{2}}\thinspace dx}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-58952a37122085ba2b62c7278278fd77_l3.png)
On sait que, si ![]() est dérivable et strictement positive, alors une primitive de la fonction
est dérivable et strictement positive, alors une primitive de la fonction ![]() est la fonction
est la fonction ![]() Par conséquent :
Par conséquent :
![Rendered by QuickLaTeX.com \[I_{3}=\int_{0}^{1}\frac{1}{2}\:\frac{2x}{1+x^{2}}\thinspace dx=\left[\frac{1}{2}\ln\left(1+x^{2}\right)\right]_{0}^{1}=\boxed{\frac{1}{2}\ln\left(2\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a502cfa27ea3c3ce37dd7a0843179cfb_l3.png)
Exemple 4
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{I_{4}=\int_{0}^{\pi/2}\sin^{2}\left(x\right)\thinspace dx}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e7f1290cc8bd63c0dda78bfa2e488bb0_l3.png)
On peut transformer l’expression ![]() en utilisant la formule de linéarisation :
en utilisant la formule de linéarisation :
![]()
![Rendered by QuickLaTeX.com \[I_{4}=\left[\frac{x}{2}-\frac{\sin\left(2x\right)}{4}\right]_{0}^{\pi/2}=\boxed{\frac{\pi}{4}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-083ad47227cf549c4b77cb2895c09b0b_l3.png)
Exemple 5
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{I_{5}=\int_{0}^{1}\frac{1}{\left(x+1\right)\left(x-2\right)}\thinspace dx}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1481fb96237c5b22c88e867899319a0d_l3.png)
Une astuce va faciliter la primitivation de la fonction ![]()
On observe que, pour tout ![]() :
:
![]()

Il est alors clair que :
![Rendered by QuickLaTeX.com \[I_{5}=\frac{1}{3}\left[\ln\left(2-x\right)-\ln\left(x+1\right)\right)]_{0}^{1}=\boxed{-\frac{2}{3}\ln\left(2\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8345589885cfcfc6d7cff984637103df_l3.png)
5 – Règles de calcul
Afin de pouvoir manipuler des intégrales, il est indispensable de connaître les quatre propriétés suivantes. Il en existe d’autres, mais on peut considérer qu’il s’agit là des propriétés de base.
Dans ce qui suit, ![]() et
et ![]() sont deux réels tels que
sont deux réels tels que ![]() .
.
1 – Linéarité
Si ![]() et
et ![]() sont continues sur
sont continues sur ![]() et si
et si ![]() alors :
alors :
![]()
- l’intégrale d’une somme de deux fonctions est égale la somme des intégrales (faire
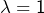 ci-dessus)
ci-dessus) - l’intégrale du produit d’une fonction par une constante est égale au produit de cette constante par l’intégrale de cette fonction (remplacer
 par la fonction nulle).
par la fonction nulle).
2 – Positivité
Si ![]() est continue sur
est continue sur ![]() et si
et si ![]() pour tout
pour tout ![]() , alors :
, alors :
![]()
3 – Croissance
En combinant linéarité et positivité, on voit aussitôt que si ![]() et
et ![]() sont continues sur
sont continues sur ![]() et si
et si ![]() pour tout
pour tout ![]() alors :
alors :
![]()
4 – Relation de Chasles
Si ![]() et si
et si ![]() est continue sur
est continue sur ![]() alors :
alors :
![]()
Remarque
En accord avec la relation de Chasles, on peut étendre la notation ![]() sans faire d’hypothèse sur les positions relatives des bornes. On considère que :
sans faire d’hypothèse sur les positions relatives des bornes. On considère que :
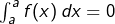
- si
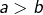 alors
alors 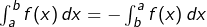
6 – Une justification intuitive
Expliquons dans cette dernière section, de manière non rigoureuse, la formule :
(![]() )
) ![]()
Si l’on note ![]() l’aire du domaine limité (à gauche) par la droite d’équation
l’aire du domaine limité (à gauche) par la droite d’équation ![]() et (à droite) par celle d’équation
et (à droite) par celle d’équation ![]() alors la dérivée de la fonction
alors la dérivée de la fonction ![]() s’obtient en calculant la limite d’un taux d’accroissement :
s’obtient en calculant la limite d’un taux d’accroissement :
![]()
Le numérateur ![]() représente l’aire d’une région qui, lorsque
représente l’aire d’une région qui, lorsque ![]() est petit, ressemble à s’y méprendre à un rectangle dont les côtés mesurent
est petit, ressemble à s’y méprendre à un rectangle dont les côtés mesurent ![]() et
et ![]()
Autrement dit, lorsque ![]() est petit :
est petit : ![]() . En passant à la limite (lorsque
. En passant à la limite (lorsque ![]() ), on trouve finalement l’égalité :
), on trouve finalement l’égalité :
![]()
Si l’on considère que ![]() représente l’aire du domaine qui s’étend de l’abscisse
représente l’aire du domaine qui s’étend de l’abscisse ![]() jusqu’à l’abscisse
jusqu’à l’abscisse ![]() alors :
alors :
![]()
De ce fait, et vu que ![]() :
:
![]()
J’espère que cet article d’introduction vous aura été utile.
N’en restez pas là ! Apprenez à intégrer par parties en lisant cet article et cherchez dès maintenant des exercices pour vous entraîner à calculer des intégrales.
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Dans la partie « 2 – Notion de primitive », on rencontre un tableau de quelques fcts usuelles et leurs primitive, or une primitive de ln(x) n’est en aucun cas 1/x
Bien vu ! Cela fait pourtant un bout de temps que cette coquille grossière traîne ici. Merci de me l’avoir signalée. Je corrige tout de suite.
J’aime beaucoup la façon dont le cours est structuré, simple et très compréhensible. J’aime votre site.
Merci pour ce sympathique commentaire 🙂 Content que ce travail vous soit utile.