Neuf énoncés d’exercices de calcul intégral (fiche 01).
Cette fiche regroupe 24 intégrales à calculer. Certaines d’entre-elles s’obtiennent de façon directe, alors que d’autres nécessitent une intégration par parties (l’intégration par changement de variable sera abordée dans une autre fiche). Le calcul d’intégrales fait partie des techniques de base auxquelles il faut s’entraîner beaucoup avant d’acquérir une maîtrise suffisante.
Comme l’a si bien écrit Georges Brassens : « sans technique, un don n’est rien qu’une sale manie ».

Calculer chacune des huit intégrales suivantes :
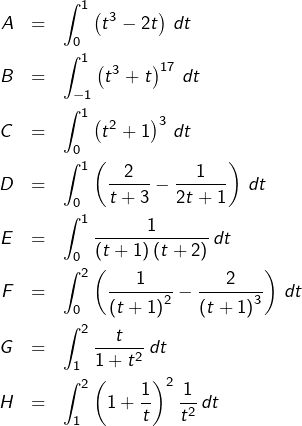
Calculer chacune des huit intégrales suivantes :
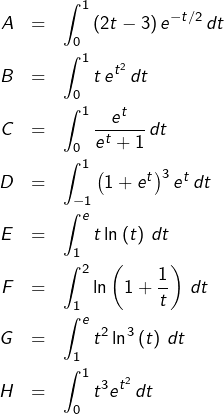

Calculer chacune des huit intégrales suivantes :
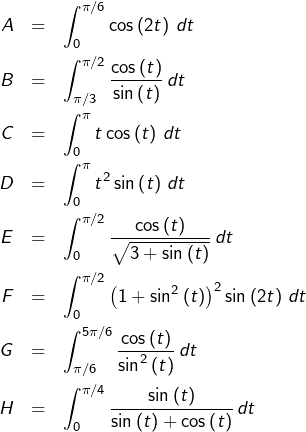
Cliquer ici pour accéder aux indications.
Cliquer ici pour accéder aux solutions.

