
Comme le titre l’indique, cet article traite des principales règles de divisibilité : certaines sont très classiques – on les rencontre dès le début du collège (parfois même un peu plus tôt); d’autres le sont nettement moins.
Si vous pensez maîtriser suffisamment les pré-requis (pour l’essentiel : notions de divisibilité et de congruence modulo un entier, écriture dans une base de numération donnée), alors je vous invite à vous rendre directement à la section 4. Et sinon, pas de panique, car j’ai prévu de reprendre toutes ces notions à zéro 🙂
1 – Diviseurs et multiples, vite fait
Avant toute chose, je vous propose de revisiter le B-A-BA concernant les notions de diviseurs et de multiples d’un nombre entier.
Vous connaissez probablement tout ça, mais c’est juste pour être sûr …
Définition
Etant donnés deux nombres entiers ![]() et
et ![]() :
:
![]() est dit multiple de
est dit multiple de ![]() lorsqu’il existe un entier
lorsqu’il existe un entier ![]() tel que
tel que ![]()
Les trois affirmations :
 est un multiple de
est un multiple de 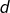
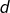 est un diviseur de
est un diviseur de 
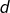 divise
divise 
expriment une seule et même propriété, que l’on note ![]() .
.
Dans le cas contraire, on note ![]()
Dans la définition ci-dessus, on insiste sur le caractère entier de ![]() : si l’on autorisait pour
: si l’on autorisait pour ![]() n’importe quelle valeur réelle, la notion perdrait tout intérêt. On peut, en effet, toujours écrire des égalités du type
n’importe quelle valeur réelle, la notion perdrait tout intérêt. On peut, en effet, toujours écrire des égalités du type ![]() mais il ne faudrait pas en déduire que
mais il ne faudrait pas en déduire que ![]() est multiple de
est multiple de ![]() …
…
Exemples
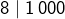 puisque
puisque 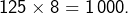
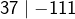 puisque
puisque 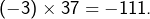
En revanche : ![]() car
car ![]() trop petit … et
trop petit … et ![]() trop grand … !
trop grand … !
On observera que :
- 0 ne divise aucun entier hormis lui-même
- 1 et -1 sont des diviseurs de tout entier
Par ailleurs, on prouve aisément les propriétés suivantes :
- Tout entier
 vérifie
vérifie 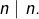
- Si deux entiers
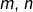 vérifient
vérifient 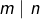 et
et 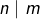 alors
alors  ou
ou 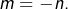
- Si trois entiers
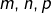 vérifient
vérifient 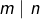 et
et 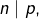 alors
alors 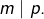
Pour les amateurs de concepts abstraits, la première et la troisième affirmation ci-dessus expriment respectivement la réflexivité et la transitivité de la relation de divisibilité dans l’ensemble ![]()
Quant à la seconde affirmation, elle dit que deux entiers qui se divisent mutuellement sont nécessairement égaux ou opposés.
En se plaçant dans ![]() au lieu de
au lieu de ![]() (c’est-à-dire en ne considérant que des entiers positifs ou nuls), les choses « s’arrangent » :
(c’est-à-dire en ne considérant que des entiers positifs ou nuls), les choses « s’arrangent » :
→ Si deux entiers naturels ![]() vérifient
vérifient ![]() et
et ![]() alors
alors ![]()
On parle, pour traduire cela, d’antisymétrie de la relation de divisibilité dans ![]()
Cette propriété est à rapprocher des deux suivantes, certainement bien connues :
- si deux nombres réels
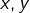 vérifient
vérifient 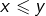 et
et 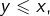 alors
alors 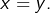
- si deux ensembles
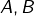 vérifient
vérifient 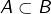 et
et 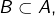 alors
alors 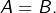
Lorsqu’on s’intéresse aux diviseurs d’un entier ![]() on peut se limiter aux diviseurs positifs puisque
on peut se limiter aux diviseurs positifs puisque ![]() équivaut à
équivaut à ![]() D’où la convention suivante :
D’où la convention suivante :

Dans toute la suite, et sauf avis contraire, lorsqu’on écrira « diviseur », il faudra comprendre « diviseur positif ».
Par exemple, les diviseurs de 48 sont au nombre de dix. Les voici dans l’ordre croissant :
![]()
Un petit test pour voir si vous suivez :
Vrai ou Faux ?
Quelques « Vrai ou Faux » pour voir si vous suivez…
- 54 possède plus de diviseurs que 24.
- 7 est un diviseur de 343.
- 1001 est un nombre premier.
- il existe des entiers naturels possédant exactement trois diviseurs.
- si un entier
 divise simultanément deux entiers
divise simultanément deux entiers  et
et 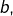 alors
alors 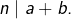
- la somme des diviseurs de 512 est inférieure à 1000.
Les réponses sont regroupées en fin d’article.
Il revient au même de dire que ![]() est multiple de
est multiple de ![]() ou que le reste de la division de
ou que le reste de la division de ![]() par
par ![]() est nul.
est nul.
Par exemple, 128588 est divisible par 17 comme on le voit en posant la division (le reste est nul) :

Maintenant, interrogeons-nous :
Question [Q]
Est-il possible de reconnaître qu’un entier est multiple d’un autre sans effectuer la division ?
Par exemple, si 5 enfants souhaitent se partager équitablement 1165 billes, ils peuvent vérifier que c’est possible en posant la division : comme ![]() alors 1165 est multiple de 5 et chaque enfant recevra 233 billes.
alors 1165 est multiple de 5 et chaque enfant recevra 233 billes.
Mais pour se convaincre que le partage équitable est possible, ils peuvent aussi observer que l’écriture décimale de 1165 se termine par un ‘5’.
Vous saviez cela. Mais sauriez-vous le justifier ?
Voici l’explication pour un nombre de 4 chiffres :
Explication (cliquer pour déplier / replier)
Prenons un nombre à quatre chiffres et notons-le ![]() ce qui signifie :
ce qui signifie :
![]()
![]()
![]()
![]() Réciproquement, si
Réciproquement, si ![]() alors :
alors :
![]()
![]()
 est multiple de 5
est multiple de 5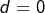 ou
ou 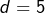
Et ceci se généralise à des entiers naturels quelconques (pas seulement ceux dont l’écriture décimale comporte quatre chiffres !). C’est ce que dit la proposition suivante :
Proposition
Etant donné un entier naturel ![]() dont le chiffre des unités est
dont le chiffre des unités est ![]() :
:
![]()
Maintenant, mettons en place un peu de théorie et nous reprendrons la question [Q] à la section 4.
2 – Un mot sur les congruences
Imaginons un fil infiniment long, sur toute la longueur duquel sont placées de petites perles, régulièrement espacées :

A côté de chaque perle, on inscrit un nombre entier : l’une des perles porte le numéro 0 et, en parcourant le fil dans un sens à partir de cette position, on voit défiler les entiers positifs 1, 2, 3, etc …
Dans le sens inverse, ce sont les entiers négatifs -1, -2, -3, etc … qui apparaissent :

Imaginons maintenant un fil hélicoïdal :

Disposons les perles sur cette hélice, de telle sorte qu’elles soient toutes sur une même verticale :

A présent, aplatissons notre fil hélicoïdal en le projetant sur un plan horizontal.
Fatalement, les perles vont toutes se retrouver au même endroit :

Et maintenant, multiplions par 5 la densité des perles sur le fil hélicoïdal :
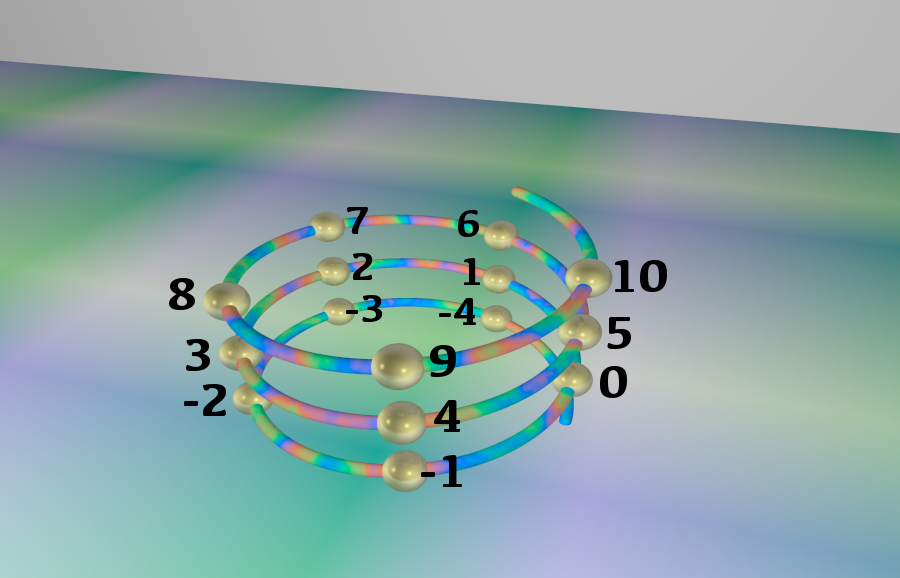
Cette fois, on observe en projection cinq zones de regroupements pour les perles… c’est-à-dire pour les entiers relatifs.
Les entiers …, -5, 0, 5, … seront tous regroupés au même endroit.
Même chose pour …, -4, 1, 6, … tout comme pour …, -3, 2, 7, … et aussi pour …, -2, 3, 8, … et enfin pour …, -1, 4, 9, …

Lorsque deux entiers se retrouvent au même endroit du cercle, on dit qu’il sont congrus l’un à l’autre modulo 5.
Cela signifie que la longueur de fil qui sépare les perles correspondantes est un multiple de la circonférence, autrement dit que la différence entre ces deux entiers est un multiple de 5.
On peut bien sûr généraliser, en remplaçant 5 par un quelconque entier ![]() …
…
Et hop ! On peut maintenant donner la :
Définition
Etant donnés un entier ![]() et deux entiers
et deux entiers ![]() on dit que
on dit que ![]() est congru à
est congru à ![]() modulo
modulo ![]() , ce qu’on note
, ce qu’on note ![]() lorsque
lorsque ![]() est multiple de
est multiple de ![]()
C’est ainsi que, par exemple :
![]()
![]()
![]()
- La première congruence résulte de
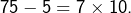
- La seconde résulte de
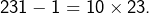
- La troisième résulte, quant à elle, de
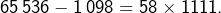
Lorsqu’on effectue la division euclidienne d’un entier ![]() par un entier
par un entier ![]() on écrit :
on écrit :
![]()
Mais attention à la réciproque ! Si trois entiers ![]() (avec
(avec ![]() vérifient
vérifient ![]() on ne peut pas en déduire que
on ne peut pas en déduire que ![]() est le reste de la division euclidienne de
est le reste de la division euclidienne de ![]() par
par ![]() C’est toutefois le cas si l’on ajoute l’hypothèse
C’est toutefois le cas si l’on ajoute l’hypothèse ![]()
Terminons cette section en présentant les règles de « compatibilité » de la congruence modulo ![]() avec l’addition et la multiplication.
avec l’addition et la multiplication.
Règle 1 – Compatibilité avec l’addition
Etant donné ![]() et
et ![]() si
si
![]()
![]()
Preuve (cliquer pour déplier / replier)
Par hypothèse, il existe des entiers ![]() tels que
tels que ![]() et
et ![]() En ajoutant membre à membre ces deux égalités, il apparaît que :
En ajoutant membre à membre ces deux égalités, il apparaît que :
![]()
Autrement dit, on peut ajouter membre à membre deux congruences, mais modulo un même entier !
Bien entendu, cela fonctionne tout aussi bien avec un nombre quelconque de congruences (toujours modulo un même entier).
En symboles, si ![]() et
et ![]() sont des entiers tels que, pour un certain
sont des entiers tels que, pour un certain ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{r}a_{i}\equiv\sum_{i=1}^{r}b_{i}\pmod{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2d29da88ee4cd5544a6ac71c2cd63c49_l3.png)
Règle 2 – Compatibilité avec la multiplication
Etant donné ![]() et
et ![]() si
si
![]()
![]()
Preuve (cliquer pour déplier / replier)
Par hypothèse, il existe des entiers ![]() tels que
tels que ![]() et
et ![]() Il s’ensuit que :
Il s’ensuit que :
![]()
On peut donc multiplier membre à membre des congruences modulo un même entier.
Plus généralement, l’hypothèse :
![]()
![Rendered by QuickLaTeX.com \[\prod_{i=1}^{r}a_{i}\equiv\prod_{i=1}^{r}b_{i}\pmod{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e4802ef082a29b89260965c53ba174b9_l3.png)
Un exemple historique
On observe que :
![]()
![]()
![]()
![]()
![]()
![]()
Il aura fallu attendre près un siècle entre la formulation par Fermat de cette conjecture et sa réfutation par Euler !..
3 – Un mot sur l’écriture décimale des entiers positifs
A l’école, nous avons appris à écrire les nombres (entiers positifs) en utilisant les dix chiffres, de 0 à 9.
De manière précise, la possibilité pour n’importe quel ![]() d’être représenté par son écriture décimale ou – plus généralement – dans une quelconque base de numération, constitue un théorème important dont voici l’énoncé :
d’être représenté par son écriture décimale ou – plus généralement – dans une quelconque base de numération, constitue un théorème important dont voici l’énoncé :
Théorème
Etant donné un entier ![]() (la « base de numération »), tout entier
(la « base de numération »), tout entier ![]() peut s’écrire :
peut s’écrire :
![Rendered by QuickLaTeX.com \[n=\sum_{k=0}^{r}c_{k}B^{k}\qquad\text{avec :}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-645809a519e80163d9c167b42af36f62_l3.png)
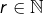
- Pour tout
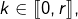
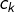 est un entier compris entre 0 et
est un entier compris entre 0 et  inclus.
inclus. 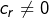
En outre, cette écriture est unique.
Les entiers ![]() sont appelés les chiffres de l’écriture de
sont appelés les chiffres de l’écriture de ![]() en base
en base ![]()
Pour celles et ceux que ça intéresse, j’ai réalisé deux petites vidéos dans lesquelles :
- ce théorème est expliqué et illustré d’exemples (vidéo 1) puis démontré rigoureusement (vidéo 2)
- l’algorithme de conversion qui en découle est expliqué en Python.
Vous pouvez visionner ces vidéos dès maintenant, si vous le souhaitez.
Ce théorème va nous servir, dès la section suivante, à formuler et / ou démontrer certaines règles de divisibilité.
4 – Règles usuelles de divisibilité
Abordons à présent le cœur du sujet.
J’en vois qui rouspètent … « c’était bien long avant de démarrer !!… ».
C’est un peu vrai, mais il fallait bien rassembler les outils appropriés pour aborder sereinement ces questions.
Etant donné un entier ![]() nous disposons de son écriture décimale (voir section précédente) :
nous disposons de son écriture décimale (voir section précédente) :
![Rendered by QuickLaTeX.com \[n=\sum_{k=0}^{r}c_{k}10^{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d5a77f84a2f82af179ab5f5ef9d36c7d_l3.png)
Tout d’abord, énonçons quelques règles, sans démonstration.
Trois règles portant sur le chiffre des unités seulement
- [
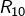 ]
]  est divisible par 10 si, et seulement si
est divisible par 10 si, et seulement si 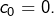
- [
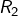 ]
]  est divisible par 2 si, et seulement si
est divisible par 2 si, et seulement si 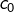 l’est, c’est-à-dire si
l’est, c’est-à-dire si 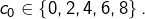
- [
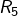 ]
]  est divisible par 5 si, et seulement si
est divisible par 5 si, et seulement si 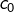 l’est, c’est-à-dire si
l’est, c’est-à-dire si 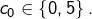
Une règle portant sur les deux derniers chiffres
- [
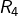 ]
]  est divisible par 4 si, et seulement si
est divisible par 4 si, et seulement si 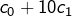 l’est, c’est à dire si l’entier formé par le chiffre des dizaines et celui des unités est multiple de 4.
l’est, c’est à dire si l’entier formé par le chiffre des dizaines et celui des unités est multiple de 4.
Une règle portant sur les trois derniers chiffres
- [
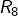 ]
]  est divisible par 8 si, et seulement si
est divisible par 8 si, et seulement si 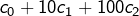 l’est, c’est à dire si l’entier formé par le chiffre des centaines, celui des dizaines et celui des unités est multiple de 8.
l’est, c’est à dire si l’entier formé par le chiffre des centaines, celui des dizaines et celui des unités est multiple de 8.
Trois règles portant sur l’ensemble des chiffres
- [
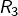 ]
]  est divisible par 3 si, et seulement si
est divisible par 3 si, et seulement si 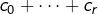 l’est.
l’est. - [
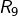 ]
]  est divisible par 9 si, et seulement si
est divisible par 9 si, et seulement si 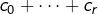 l’est.
l’est. - [
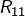 ]
]  est divisible par 11 si, et seulement si
est divisible par 11 si, et seulement si 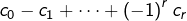 l’est (autrement dit si la somme alternée des chiffres est multiple de 11).
l’est (autrement dit si la somme alternée des chiffres est multiple de 11).
L’intérêt de ce genre de critère est clair : ils nous permettent de savoir si un entier est multiple de 3 (ou de 9, ou de 11, etc…) en effectuant considérablement moins de calculs que si l’on posait la division. Et cet écart est d’autant plus marqué que l’écriture décimale de l’entier testé comporte davantage de chiffres.
Pour les preuves des règles [ ![]() ] et [
] et [ ![]() ], je vous renvoie à la fiche n° 1 sur la divisibilité.
], je vous renvoie à la fiche n° 1 sur la divisibilité.
La règle [ ![]() ] est établie à la section 5 … mais n’y allez pas tout de suite !
] est établie à la section 5 … mais n’y allez pas tout de suite !
Cherchez un peu 🙂
Les autres règles sont très simples à démontrer.
5 – L’affaire 1001
Tout d’abord, un constat :
![]()
Nous allons nous appuyer sur cette égalité pour élaborer deux tests de divisibilité, l’un par 7 et l’autre par 13.

Considérons un entier positif ![]() et son écriture en base 1000.
et son écriture en base 1000.
C’est vrai que, dit comme ça, c’est un peu étrange … Mais après tout, le théorème énoncé à la section 3 est valable en particulier pour ![]() .
.
On écrit donc :
![Rendered by QuickLaTeX.com \[n=\sum_{k=0}^{s}p_{k}\thinspace1000^{k}\qquad\left(\heartsuit\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-eb4027048bbf358a3a03cc41743b64b4_l3.png)
Ce sont les chiffres de l’écriture de ![]() en base 1000. Par exemple, si
en base 1000. Par exemple, si ![]() (écriture décimale), alors
(écriture décimale), alors ![]() et :
et :
![]()
Mais revenons au cas général. Comme ![]() on déduit de
on déduit de ![]() que :
que :
![Rendered by QuickLaTeX.com \[n\equiv\sum_{k=0}^{s}\left(-1\right)^{k}p_{k}\pmod{7}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9d18369338ce266ab352a7552f8edd16_l3.png)
Il en découle les deux règles suivantes :
Règles de divisibilité par 7 et 13
- [
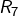 ]
]  est divisible par 7 si, et seulement
est divisible par 7 si, et seulement  l’est
l’est - [
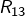 ]
]  est divisible par 13 si, et seulement
est divisible par 13 si, et seulement  l’est
l’est
Voyons un exemple. Considérons l’entier ![]() pour lequel
pour lequel ![]() et
et
![]()
Calculons :
![]()
Comme
Encore un exemple, avec ![]()
Cette fois, ![]() et :
et :
![]()
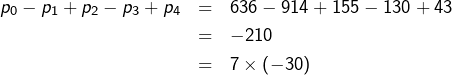
Un dernier mot à ce sujet : la congruence ![]() est aussi vraie. Alors pourquoi ne pas énoncer un test similaire de divisibilité par
est aussi vraie. Alors pourquoi ne pas énoncer un test similaire de divisibilité par ![]() ?
?
Tout simplement parce qu’il y a plus simple. Il suffit de voir que ![]() et donc, en utilisant l’écriture décimale :
et donc, en utilisant l’écriture décimale :
![Rendered by QuickLaTeX.com \[n=\sum_{k=0}^{r}c_{k}\thinspace10^{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3543315d0f3f88902843c53f7f75d297_l3.png)
![Rendered by QuickLaTeX.com \[n\equiv\sum_{k=0}^{r}\left(-1\right)^{k}c_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7a131614f696488605608cd0ac05705c_l3.png)
6 – Les tests itérés
Etant un donné un entier naturel ![]() notons
notons ![]() le nombre des dizaines et
le nombre des dizaines et ![]() le chiffre des unités, de sorte que
le chiffre des unités, de sorte que ![]()
Par exemple si ![]() alors
alors ![]() et
et ![]()
On décrit ici un ensemble de règles ayant en commun de ramener la question « ![]() est-il divisible par
est-il divisible par ![]() » à la question «
» à la question « ![]() est-il divisible par
est-il divisible par ![]() « , où
« , où ![]() désigne un entier convenablement choisi et qui dépend de
désigne un entier convenablement choisi et qui dépend de ![]()
J’ai adopté la terminologie de « tests itérés » car, en principe, on aura ![]() ce qui va nous conduire à itérer le mécanisme, c’est-à-dire à construire une séquence décroissante d’entiers :
ce qui va nous conduire à itérer le mécanisme, c’est-à-dire à construire une séquence décroissante d’entiers :
![]()
![]()
![]()
Si vous connaissez une dénomination officielle pour ce type de règle, je vous remercie par avance de m’en informer (en passant par exemple par le formulaire de contact).
Avant de présenter cette méthode dans le cas général, examinons quatre cas particuliers (divisibilité par 7, par 13, par 17 ou par 19) :
Règle itérée pour 7
Le cas ![]()
On constate que :
![]()
d’où l’on déduit que si
Par ailleurs :
![]()
d’où l’on déduit que si
![]()
Exemple
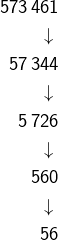
or
Remarque
lorsque l’un des entiers de la séquence se termine par un 0, on peut directement supprimer ce chiffre et passer à l’entier suivant (ici, de 560 à 56). En effet, ![]() et
et ![]() sont premiers entre eux, donc
sont premiers entre eux, donc ![]() pour tout entier
pour tout entier ![]() .
.
Règle itérée pour 13
Le cas ![]()
On constate que :
![]()
Par ailleurs :
![]()
![]()
Exemple

or
Remarque
A partir de l’entier 26, l’itération de produit rien de neuf, puisque![]()
Règle itérée pour 17
Le cas ![]()
On constate que :
![]()
Par ailleurs :
![]()
![]()
Exemple
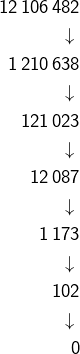
or
Règle itérée pour 19
Le cas ![]()
On constate que :
![]()
d’où l’on déduit que si
Par ailleurs :
![]()
d’où l’on déduit que si
![]()
Exemple

or
Plus généralement, si ![]() est un entier premier avec
est un entier premier avec ![]() alors l’identité de Bézout garantit l’existence de deux entiers relatifs
alors l’identité de Bézout garantit l’existence de deux entiers relatifs ![]() tels que
tels que ![]() On voit alors que :
On voit alors que :
![]()
Par ailleurs :
![]()
ce qui prouve l’implication réciproque. Bref :
![]()
Remarque
Ce critère n’a d’intérêt que si l’entier testé est remplacé par un entier plus petit, c’est-à-dire si ![]() , condition qui est effectivement remplie dans chacun des quatre cas détaillés plus haut.
, condition qui est effectivement remplie dans chacun des quatre cas détaillés plus haut.
Annexe : Réponses aux Vrai / Faux
54 possède plus de diviseurs que 24.
C’est FAUX, il en possède autant !
Diviseurs de ![]() :
:
![]()
![]()
![]()
Avec ces notations, le nombre de diviseurs de ![]() est donné par le produit :
est donné par le produit :
![]()
![]()
![]()
7 est un diviseur de 343.
C’est VRAI, puisque :
![]()
1001 est un nombre premier.
C’est FAUX. On constate que :
![]()
Le test de divisibilité par ![]() ou par
ou par ![]() permettait de le découvrir, puisque la somme alternée des chiffres en base
permettait de le découvrir, puisque la somme alternée des chiffres en base ![]() est nulle (voir section 5) !
est nulle (voir section 5) !
Il existe des entiers naturels possédant exactement trois diviseurs.
C’est VRAI. En effet, si ![]() est un nombre premier et si
est un nombre premier et si ![]() alors les diviseurs de
alors les diviseurs de ![]() sont les
sont les ![]() pour
pour ![]() En particulier, les diviseurs de
En particulier, les diviseurs de ![]() sont
sont ![]()
![]() et
et ![]()
Les carrés de nombres premiers sont d’ailleurs les seuls entiers qui possèdent exactement trois diviseurs ! En effet, d’après la formule vue plus haut (voir le premier « Vrai ou Faux »), il faut que ![]() ce qui impose que l’un des
ce qui impose que l’un des ![]() vaut
vaut ![]() et tous les autres valent
et tous les autres valent ![]() autrement dit que
autrement dit que ![]() est de la forme
est de la forme ![]() avec
avec ![]() premier.
premier.
Si un entier ![]() divise simultanément deux entiers
divise simultanément deux entiers ![]() et
et ![]() alors
alors ![]()
C’est VRAI. En effet, si ![]() et
et ![]() alors
alors ![]() Tout simplement.
Tout simplement.
La somme des diviseurs de 512 est inférieure à 1000.
C’est FAUX.
On peut certainement faire le calcul « bêtement ».
Mais on peut aussi observer que ![]() et que, par conséquent, les diviseurs de
et que, par conséquent, les diviseurs de ![]() sont les
sont les ![]() pour
pour ![]()
En utilisant la formule donnant la somme d’une progression géométrique (programme de première), on trouve :
![Rendered by QuickLaTeX.com \[1+2+4+8+16+32+64+128+256+512=\sum_{k=0}^{9}2^{k}=2^{10}-1=1\thinspace023\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c9e728c25880bf51b0576aae4c7893b1_l3.png)
Merci de m’avoir lu jusqu’au bout 🙂
Si vous souhaitez chercher des exercices en rapport avec le thème de la divisibilité, vous pouvez jeter un coup d’œil par ici.
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Bonsoir Monsieur,
Dans l’explication à dérouler via un clic, juste avant la section 2, un « n=5(q+1) » est resté en « affichage code latex ».
Bien à vous
Bien vu et merci 🙂 C’est rectifié.
Bonjour,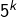 ou
ou 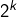 :
:
Merci pour votre article très complet. Je vous propose également mon test itéré de divisibilité par
Divisibilité par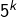 :
:
Si le nombre se termine par 0, supprimer le 0 et chercher la divisibilité par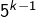 .
.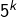 pour que le nombre se termine par 0.
pour que le nombre se termine par 0.
Sinon, ajouter ou retrancher
Divisibilité par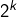 :
:
Si le nombre se termine par 0, supprimer le 0 et chercher la divisibilité par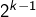 .
.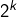 ou
ou 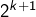 pour que le nombre se termine par 0.
pour que le nombre se termine par 0.
Sinon, ajouter ou retrancher
Merci beaucoup, des techniques très intéressantes et des découvertes pour ma part! 🙂
toujours très bon mais souhaite d’autres domaines d’intérêt : par exemple, méthode et technique de recherche de plans stables par un endomorphisme de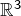 …
…
Merci pour ce commentaire. Mon prochain article sera donc consacré à une question d’algèbre linéaire 🙂