On définit deux suites d’entiers naturels 
et 
par les relations suivantes :
![\[a_{1}=1,\quad a_{2}=2,\quad\forall n\geqslant2,\,a_{n+1}=a_{n}+a_{n-1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e3258f6510cea910fa9212d3effacf36_l3.png "Rendered by QuickLaTeX.com")
![\[b_{1}=2,\quad b_{2}=1,\quad\forall n\geqslant2,\,b_{n+1}=b_{n}+b_{n-1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-02b6e96a7b17c221e19948e178685288_l3.png "Rendered by QuickLaTeX.com")
Quels sont les entiers naturels qui sont présents simultanément dans chacune d’elles ?
Une solution est disponible ici
Challenge 82 : Fibonacci & Lucas
On définit deux suites d’entiers naturels et par les relations suivantes :
Quels sont les entiers naturels qui sont présents simultanément dans chacune d’elles ?
Une solution est disponible ici
Un indice : remarquez que pour n plus grand ou égal à 5,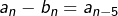
.