Challenge 7 : Maximum de ln(1 + x) ln(1 + 1/x) Auteur/autrice de la publication :René Adad Post published:19 décembre 2017 Post category:Challenge Ce challenge est nettement plus accessible que les précédents 🙂 Il s’agit de calculer le maximum, pour de l’expression : Une solution est disponible ici J’aime ça :J’aime chargement…Partager cet article1 Étiquettes : blog-de-maths, challenge, convexité, dérivée, inégalité, logarithme, Math-OS, MP*, MPSI, PCSI, prépas, sens de variation Read more articles Article précédentChallenge 6 : Majoration d’une somme de série Article suivantChallenge 8 : une histoire de bitangente Vous devriez également aimer Challenge 92 : Une bien curieuse égalité 21 février 2026 Challenge 53 : Encadrement pour 1/sin²(x) – 1/x² 6 octobre 2020 Challenge 23 : Une intrigue polynomiale 5 février 2019 Cet article a 2 commentaires Paul 23 Mar 2020 Répondre Petite correction de la solution pour tout , . Il me semble que c’est faux car si par exemple cela voudrait dire que . René Adad 23 Mar 2020 Répondre Merci de m’avoir cette coquille, qui est à présent corrigée. Laisser un commentaire Annuler la réponseCommentEnter your name or username to comment Enter your email address to comment Enter your website URL (optional) Enregistrer mon nom, mon e-mail et mon site dans le navigateur pour mon prochain commentaire. Prévenez-moi de tous les nouveaux commentaires par e-mail. Prévenez-moi de tous les nouveaux articles par e-mail. Δ
Paul 23 Mar 2020 Répondre Petite correction de la solution pour tout , . Il me semble que c’est faux car si par exemple cela voudrait dire que .
Petite correction de la solution pour tout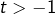 ,
, 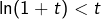 . Il me semble que c’est faux car si
. Il me semble que c’est faux car si 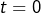 par exemple cela voudrait dire que
par exemple cela voudrait dire que 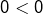 .
.
Merci de m’avoir cette coquille, qui est à présent corrigée.