icone-challenge-math-OS

Solution pour le challenge 7

On étudie les variations de la fonction définie sur ]0,+\infty[ par :

    \[\boxed{f(x)=\ln(1+x)\ln\left(1+\frac 1x\right)}\]

Pour cela, on cherche le signe de sa dérivée.

Pour tout x>0 :
f'\left(x\right)=\frac{1}{1+x}\ln\left(1+\frac{1}{x}\right)-\frac{1}{x\left(1+x\right)}\ln\left(1+x\right)
Cette expression est du signe de :
g\left(x\right)=x\ln\left(1+\frac{1}{x}\right)-\ln\left(1+x\right)
que l’on dérive à son tour pour obtenir :
g'\left(x\right)=\frac{x}{1+x}\ln\left(1+\frac{1}{x}\right)-\frac{1}{1+x}
Cette expression est du signe de :
h\left(x\right)=\ln\left(1+\frac{1}{x}\right)-\frac{1}{x}

Or, il est connu que pour tout t>1 :

    \[\fcolorbox{black}{myBlue}{\ensuremath{\ln\left(1+t\right)\leqslant t}}\qquad\left(\spadesuit\right)\]

On en déduit que h\left(x\right)<0, pour tout x>0; et donc que g décroît. Comme g\left(1\right)=0, on en déduit que g est positive sur \left]0,1\right[ et négative sur \left]1,+\infty\right[.

Par conséquent f croît sur \left]\text{0,1}\right] et décroît sur \left[1,+\infty\right[.

Finalement, f présente un maximum atteint pour x=1. Ce maximum est f\left(1\right)=\ln^{2}\left(2\right).

En conclusion, pour tout x>0 :
\boxed{\ln\left(1+x\right)\ln\left(1+\frac{1}{x}\right)\leqslant\ln^{2}\left(2\right)}
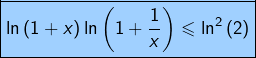
avec égalité seulement pour x=1.

Remarque

En appliquant deux fois \left(\spadesuit\right), on voit directement que pour tout x>0 :
\ln\left(1+x\right)\ln\left(1+\frac{1}{x}\right)\leqslant1
mais cette majoration est de moins bonne qualité (car \ln^{2}\left(2\right)\simeq0,48).

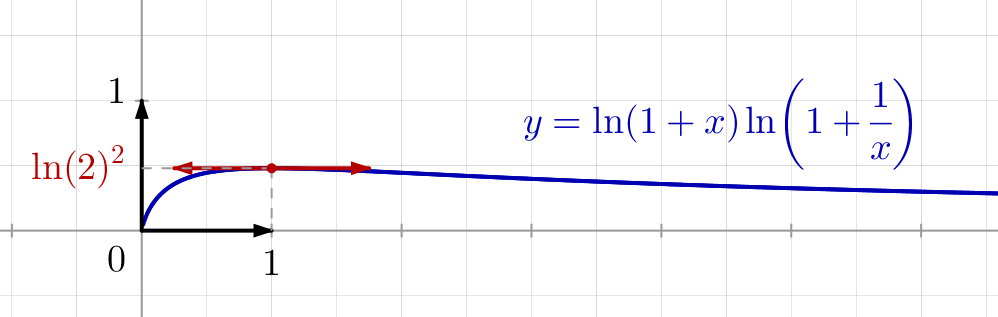
L’illustration ci-dessous montre le graphe de f, construit en repère orthonormal :

graphe-de-f

Pour consulter l’énoncé, c’est ici

Partager cet article
1   

Laisser un commentaire