Qu'est-ce qu'une factorielle ? (Partie 2)

Pré-requis : intégration par parties, suites numériques équivalentes, calcul de développements limités, séries numériques (séries de Riemann, règle des équivalents).

1 – Une factorielle, c’est grand… mais grand comment ?

Si vous n’avez pas encore lu l’article « Qu’est-ce qu’une factorielle ? Partie 1 », lisez-le 🙂

On y trouve, pour l’essentiel, une interprétation étonnante de l’entier $52!,$ dont la taille gigantesque dépasse largement ce que l’intuition nous permet d’appréhender.

Je vous propose maintenant d’aller rendre visite à une formule célèbre, attribuée au mathématicien écossais James Stirling (1692-1770), qui donne une estimation asymptotique de $n!$ lorsque $n$ tend vers l’infini :

$\fcolorbox{black}{myBlue}{$n!\sim\left(\frac{n}{e}\right)^{n}\sqrt{2\pi n}$}$

Le symbole $\sim$ se lit « est équivalent à » et signifie que le rapport des deux membres tend vers 1. Autrement dit, nous allons prouver que :

$\boxed{\lim_{n\rightarrow\infty}\frac{n!\thinspace e^{n}}{n^{n}\sqrt{n}}=\sqrt{2\pi}}$

😯 Une formule pour le moins surprenante !… En effet, la factorielle d’un entier $n$ est par définition égale au produit des entiers de 1 à $n$ : c’est donc une quantité définie très simplement et de manière purement arithmétique. Pourtant, lorsqu’on se penche sur son comportement à l’infini, on voit débarquer deux « stars » de l’analyse mathématique, à savoir les nombres π et e.

Afin d’établir ce résultat, intéressons-nous au préalable à une suite d’intégrales…

La $n-$ ème intégrale de Wallis, notée $W_{n},$ est définie pour tout $n\in\mathbb{N}$ par :

$\boxed{W_{n}=\int_{0}^{\pi/2}\sin^{n}\left(t\right)\thinspace dt}$

Dans ce qui suit, nous allons :

d’une part, obtenir un équivalent de 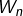$W_{n}$ lorsque $n$ tend vers l’infini,
d’autre part, établir une formule explicite pour 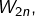$W_{2n},$ qui fait intervenir des factorielles.

C’est en combinant ces deux points que nous démontrerons la formule de Stirling.

2 – Relation de récurrence pour les intégrales de Wallis

On commence par mettre en évidence une relation de récurrence vérifiée par la suite $\left(W_{n}\right)_{n\in\mathbb{N}}.$ Pour cela, on intègre par parties pour $n\geqslant2,$ en posant :

$u\left(t\right)=\sin^{n-1}\left(t\right)\qquad\text{et}\qquad v'\left(t\right)=\sin\left(t\right)$

$u'\left(t\right)=\left(n-1\right)\sin^{n-2}\left(t\right)\cos\left(t\right)\qquad\text{et}\qquad v\left(t\right)=-\cos\left(t\right)$

ce qui donne :

$W_{n}=\left[-\sin^{n-1}\left(t\right)\cos\left(t\right)\right]_{0}^{\pi/2}+\left(n-1\right)\int_{0}^{\pi/2}\sin^{n-2}\left(t\right)\cos^{2}\left(t\right)\thinspace dt$

Le terme entre crochets est nul puisque $\sin\left(0\right)=\cos\left(\frac{\pi}{2}\right)=0.$ Par ailleurs, en remplaçant $\cos^{2}\left(t\right)$ par $1-\sin^{2}\left(t\right)$ dans la dernière intégrale, il vient :

$W_{n}=\left(n-1\right)\int_{0}^{\pi/2}\sin^{n-2}\left(t\right)\left(1-\sin^{2}\left(t\right)\right)\thinspace dt=\left(n-1\right)\left(W_{n-2}-W_{n}\right)$

Nous avons prouvé que, pour tout $n\geqslant2$ :

( $\star$ ) $\fcolorbox{black}{myBlue}{$nW_{n}=\left(n-1\right)W_{n-2}$}$

Cette relation de récurrence ramène le calcul de $W_{n}$ à celui de $W_{n-2},$ puis de $W_{n-4}$ … etc … et finalement de $W_{0}$ (si $n$ est pair) ou de $W_{1}$ (sinon).

On calcule donc, une fois pour toutes :

$\boxed{W_{0}=\int_{0}^{\pi/2}\thinspace dt=\frac{\pi}{2}}\qquad\text{et}\qquad\boxed{W_{1}=\int_{0}^{\pi/2}\sin\left(t\right)\thinspace dt=1}$

après quoi, le calcul numérique de $W_{n}$ pour une petite valeur de $n$ est un jeu d’enfant.

Par exemple :

$W_{7}=\frac{6}{7}\thinspace W_{5}=\frac{6}{7}\times\frac{4}{5}\thinspace W_{3}=\frac{6}{7}\times\frac{4}{5}\times\frac{2}{3}\thinspace W_{1}\qquad\text{soit : }W_{7}=\frac{16}{35}$

3 – Equivalent de la n-ème intégrale de Wallis

La suite $\left(W_{n}\right)_{n\geqslant0}$ est décroissante. En effet, pour tout $n\in\mathbb{N}$ :

$W_{n+1}-W_{n}=\int_{0}^{\pi/2}\sin^{n}\left(t\right)\left(\sin\left(t\right)-1\right)\thinspace dt$

Or d’une part $\sin\left(t\right)\geqslant0$ pour tout $t\in\left[0,\pi\right]$ (et, a fortiori, pour tout $t\in\left[0,\frac{\pi}{2}\right]$ ) et, d’autre part $\sin\left(t\right)\leqslant1$ pour tout réel $t.$ La différence $W_{n+1}-W_{n}$ est donc négative, en tant qu’intégrale d’une fonction négative.

Il s’ensuit que, pour tout $n\in\mathbb{N}^{\star}$ :

$\fcolorbox{black}{myBlue}{$W_{n+1}\leqslant W_{n}\leqslant W_{n-1}$}$

Les intégrales de Wallis sont toutes strictement positives, car une fonction continue, positive et qui n’est pas identiquement nulle possède une intégrale strictement positive. Autre justification possible … en utilisant la minoration

$\forall t\in\left[0,\frac\pi 2\right],\,\sin(t)\geqslant\frac{2t}\pi$

on voit que, pour tout $n\in\mathbb{N}$ :

$W_n\geqslant\int_0^{\pi/2}\left(\frac{2t}\pi\right)^n\thinspace dt=\frac{\pi}{2(n+1)}>0$

Bref, on peut diviser chaque membre de l’encadrement précédent par $W_{n-1},$ ce qui donne :

$\frac{W_{n+1}}{W_{n-1}}\leqslant\frac{W_{n}}{W_{n-1}}\leqslant1$

Compte tenu de la relation de récurrence $\left(\star\right),$ ce dernier encadrement peut aussi s’écrire :

$\frac{n}{n+1}\leqslant\frac{W_{n}}{W_{n-1}}\leqslant1$

et vu que $\lim_{n\rightarrow\infty}\frac{n}{n+1}=1,$ le théorème d’encadrement (alias « théorème des gendarmes ») nous montre que :

( $\diamondsuit$ ) $\fcolorbox{black}{myBlue}{$\displaystyle{\lim_{n\rightarrow\infty}\frac{W_{n}}{W_{n-1}}=1}$}$

Par ailleurs, en multipliant chaque membre de $\left(\star\right)$ par $W_{n-1},$ on obtient :

$nW_{n}W_{n-1}=\left(n-1\right)W_{n-1}W_{n-2}$

ce qui montre que la suite $\left(nW_{n}W_{n-1}\right)_{n\geqslant1}$ est constante. Cette constante n’est autre que le premier terme de la suite, c’est-à-dire $1\times W_{1}\times W_{0}.$ Or, nous connaissons les valeurs de $W_{0}$ et $W_{1}$ (elles ont été calculées à la section 2); on voit ainsi que :

( $\heartsuit$ ) $\fcolorbox{black}{myBlue}{$\displaystyle{\forall n\geqslant1,\:nW_{n}W_{n-1}=\frac{\pi}{2}}$}$

Pour finir, on peut écrire artificiellement, pour tout $n\in\mathbb{N}^{\star}$ :

$nW_{n}^{2}=nW_{n}W_{n-1}\;\frac{W_{n}}{W_{n-1}}$

et donc, d’après $\left(\diamondsuit\right)$ et $\left(\heartsuit\right)$ :

$nW_{n}^{2}\sim\frac{\pi}{2}$

C’est-à-dire :

$\fcolorbox{black}{myBlue}{$\displaystyle{W_{n}\sim\sqrt{\frac{\pi}{2n}}}$}$

Cet équivalent indique une convergence « plutôt lente » vers 0 pour la suite $\left(W_n\right)_{n\geqslant0}$ .

4 – Calcul explicite des intégrales de Wallis

En exploitant la relation de récurrence $\left(\star\right),$ on peut expliciter $W_{n}$ en distinguant deux cas, selon la parité de $n.$ Intéressons-nous au cas où $n$ est pair …

On calcule successivement :

$W_{2}=\frac{1}{2}\thinspace W_{0}\qquad W_{4}=\frac{3\times1}{4\times2}\thinspace W_{0}\qquad W_{6}=\frac{5\times3\times1}{6\times4\times2}\thinspace W_{0}\qquad\text{etc...}$

ce qui laisse deviner, pour tout $p\in\mathbb{N},$ la formule générale :

$W_{2p}=\frac{\left(2p-1\right)\left(2p-3\right)\cdots3\times1}{2p\left(2p-2\right)\cdots4\times2}\thinspace W_{0}\qquad\spadesuit$

Cette formule se prouve aisément par récurrence (non détaillé).

La fraction au second membre de $\left(\spadesuit\right)$ fait intervenir des produits d’entiers qui se suivent de $2$ en $2$ … Il ne reste donc pas grand chose à faire pour qu’apparaissent des factorielles !

On peut en effet multiplier le numérateur et le dénominateur de cette fraction par le produit $2p\left(2p-2\right)\cdots4\times2.$

Ceci a pour effet de « boucher les trous » au numérateur et de faire apparaître la factorielle de $2p.$ On tombe ainsi sur :

$W_{2p}=\frac{\left(2p\right)!}{\left[2p\left(2p-2\right)\cdots4\times2\right]^{2}}\thinspace W_{0}$

c’est-à-dire :

$\fcolorbox{black}{myBlue}{$\displaystyle{W_{2p}=\frac{\left(2p\right)!\thinspace\pi}{2^{2p+1}\left(p!\right)^{2}}}$}$

Par exemple :

$W_{20}=\frac{20!\:\pi}{2^{21}\left(10!\right)^{2}}=\frac{46189\thinspace\pi}{524288}$

Remarque 1

Ce calcul classique fait l’objet de l’exercice n° 2 de cette fiche d’exercices sur la factorielle. En liaison avec la formule de Stirling, on pourra aussi regarder l’exercice n° 5 de cette même fiche.

Remarque 2

Un calcul similaire montre que, pour tout $p\in\mathbb{N}$ :

$\boxed{W_{2p+1}=\frac{2^{2p}\left(p!\right)^{2}}{\left(2p+1\right)!}}$

mais on n’en aura pas besoin dans la suite de cet article.

5 – La formule de Stirling

Comme cela a été indiqué en début d’article, nous souhaitons démontrer que :

$\fcolorbox{black}{myBlue}{$\displaystyle{\lim_{n\rightarrow\infty}\frac{n!\thinspace e^{n}}{n^{n}\sqrt{n}}=\sqrt{2\pi}}$}$

Pour cela, nous procéderons en deux temps :

[Etape 1] Nous allons d’abord prouver que la suite de terme général
$u_{n}=\frac{n!\thinspace e^{n}}{n^{n}\sqrt{n}}$
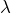est convergente (étape 1-A) et que sa limite $\lambda$ est non nulle (étape 1-B),
[Etape 2] ensuite, nous calculerons 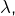$\lambda,$ en nous servant de ce que nous avons appris au sujet des intégrales de Wallis.

Pour des raisons de type « pédagogique », l’étape 1 sera traitée deux fois :

→ une première fois avec des outils de niveau « T+ » (c’est-à-dire de niveau Terminale avec un enseignement mathématique renforcé, mais avec une mise en œuvre technique supérieure à ce qui se pratique communément dans cette classe)

→ une seconde fois avec des outils de niveau 1ère / 2ème année d’enseignement supérieur (développements limités, séries numériques et règles usuelles de convergence), ce qui aura pour effet de raccourcir significativement la démonstration.

Détail étape 1-A (niveau T+) (cliquer pour déplier / replier)

Pour montrer que la suite $\left(u_{n}\right)_{n\geqslant1}$ converge, il suffit de voir qu’elle est décroissante (comme elle est d’évidence minorée par $0,$ le célèbre théorème « toute suite réelle décroissante et minorée converge » pourra s’appliquer).

Pour cela, comparons à 1 le quotient de deux termes consécutifs. Pour tout $n\geqslant1$ :

$\begin{eqnarray*}\frac{u_{n+1}}{u_{n}} & = & \frac{\left(n+1\right)!\thinspace e^{n+1}}{\left(n+1\right)^{n+1}\sqrt{n+1}}\:\frac{n^{n}\sqrt{n}}{n!\thinspace e^{n}}\cr\noalign{\vspace{8pt}}& = & \frac{\left(n+1\right)!}{n!}\thinspace\frac{e^{n+1}}{e^{n}}\thinspace\frac{n^{n}}{\left(n+1\right)\left(n+1\right)^{n}}\sqrt{\frac{n}{n+1}}\cr\noalign{\vspace{8pt}}& = & e\thinspace\left(\frac{n}{n+1}\right)^{n}\sqrt{\frac{n}{n+1}}\cr\noalign{\vspace{8pt}}& = & e\thinspace\left(\frac{n}{n+1}\right)^{n+\frac{1}{2}}\end{eqnarray*}$

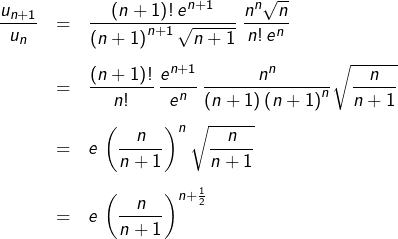
Il revient au même de déterminer le signe de $\ln\left(\frac{u_{n+1}}{u_{n}}\right)$ , c’est-à-dire de :

$1+\left(n+\frac{1}{2}\right)\ln\left(\frac{n}{n+1}\right)=\left(n+\frac{1}{2}\right)F\left(n\right)\qquad\left(\natural\right)$

où l’on a posé, pour tout $t>0$ :

$F\left(t\right)=\frac{1}{t+\frac{1}{2}}+\ln\left(\frac{t}{t+1}\right)$

La fonction F est dérivable sur $\left]0,+\infty\right[$ et sa dérivée est donnée par :

$F'\left(t\right)=-\frac{1}{\left(t+\frac{1}{2}\right)^{2}}+\frac{1}{t}-\frac{1}{t+1}=\frac{-t\left(t+1\right)+\left(t+\frac{1}{2}\right)^{2}}{t\left(t+1\right)\left(t+\frac{1}{2}\right)^{2}}$

Après simplification :

$F'\left(t\right)=\frac{1}{4t\left(t+1\right)\left(t+\frac{1}{2}\right)^{2}}>0$

ce qui montre la stricte croissance de F. Comme $\lim_{t\rightarrow+\infty}F\left(t\right)=0,$ on en déduit que $F\left(t\right)<0$ pour tout $t>0.$ Ainsi :

$\forall n\in\mathbb{N}^{\star},\thinspace\ln\left(\frac{u_{n+1}}{u_{n}}\right)<0$

Autrement dit :

$\forall n\in\mathbb{N}^{\star},\thinspace\frac{u_{n+1}}{u_{n}}<1$

La décroissance de la suite $\left(u_{n}\right)_{n\geqslant1}$ est établie et sa convergence en résulte.

Détail étape 1-B (niveau T+) (cliquer pour déplier / replier)

Nous allons avoir recours à un :

Lemme

Pour tout $t\in\left[0,1\right[$ :

$-\ln\left(1-t\right)\leqslant t+\frac{t^{2}}{2}+\frac{t^{3}}{3\left(1-t\right)}$

La preuve de ce lemme est reportée en ANNEXE.

Repartons de la formule $\left(\natural\right)$ établie plus haut. Pour tout $n\geqslant1$ :

$\ln\left(u_{n+1}\right)-\ln\left(u_{n}\right)=1+\left(n+\frac{1}{2}\right)\ln\left(\frac{n}{n+1}\right)$

Nous allons minorer cette expression, ce qui donnera (après sommation télescopique), une minoration de $\ln\left(u_{n}\right).$
Nous constaterons qu’il est possible de minorer $\ln\left(u_{n}\right)$ par une certaine constante $K.$
Il en résultera une minoration de $u_{n}$ par une constante strictement positive (à savoir $e^{K}$ ), d’où la non-nullité de la limite $\lambda.$

Il faut à présent mettre les mains dans le cambouis …

La formule ci-dessus peut s’écrire :

$\ln\left(u_{n+1}\right)-\ln\left(u_{n}\right)=1+\left(n+\frac{1}{2}\right)\ln\left(1-\frac{1}{n+1}\right)$

Donc, d’après le lemme :

$\ln\left(u_{n+1}\right)-\ln\left(u_{n}\right)\geqslant1-\left(n+\frac{1}{2}\right)\left(\frac{1}{n+1}+\frac{1}{2\left(n+1\right)^{2}}+\frac{1}{3\left(n+1\right)^{3}\left(1-\frac{1}{n+1}\right)}\right)$

c’est-à-dire (après un peu de calcul…) :

$\ln\left(u_{n+1}\right)-\ln\left(u_{n}\right)\geqslant-\frac{n+2}{12n\left(n+1\right)^{2}}$

d’où, en majorant $n+2$ par $2n+2$ :

$\ln\left(u_{n+1}\right)-\ln\left(u_{n}\right)\geqslant-\frac{1}{6n\left(n+1\right)}=-\frac{1}{6}\left(\frac{1}{n}-\frac{1}{n+1}\right)$

A présent, ajoutons membre à membre ces inégalités pour les indices $1$ à $n-1$ (pour $n\geqslant2$ ) :

$\ln\left(u_{n}\right)-\ln\left(u_{1}\right)\geqslant-\frac{1}{6}\left(1-\frac{1}{n}\right)$

Comme $u_{1}=e,$ on en déduit que :

$\forall n\geqslant1,\:\ln\left(u_{n}\right)\geqslant\frac{5}{6}+\frac{1}{6n}>\frac{5}{6}$

et donc :

$\boxed{\forall n\geqslant1,\:u_{n}\geqslant e^{\frac{5}{6}}}$

On est maintenant certain que la limite $\lambda$ de la suite $\left(u_{n}\right)_{n\geqslant1}$ est non nulle.

Détail étapes 1-A & 1-B (niveau Sup) (cliquer pour déplier / replier)

Pour qu’une suite $\left(t_{n}\right)_{n\geqslant1}$ de réels strictement positifs converge vers une limite $\lambda$ non nulle, il suffit que la suite $\left(\ln\left(t_{n}\right)\right)_{n\geqslant1}$ soit convergente. En effet, en notant $\alpha=\lim_{n\rightarrow\infty}\ln\left(t_{n}\right),$ on aura (par continuité de la fonction exponentielle) : $\lambda=e^{\alpha}>0.$

Par ailleurs, pour qu’une suite $\left(a_{n}\right)_{n\geqslant1}$ soit convergente, il suffit que la série $\sum_{n\geqslant1}\left(a_{n+1}-a_{n}\right)$ le soit. En effet, par télescopage des termes :

$\forall n\geqslant1,\;a_{n}=a_{1}+\sum_{k=1}^{n-1}\left(a_{k+1}-a_{k}\right)$

Intéressons-nous donc à la série de terme général $\ln\left(\frac{u_{n+1}}{u_{n}}\right).$ On sait que pour tout $n\geqslant1$ :

$\frac{u_{n+1}}{u_{n}}=e\thinspace\left(\frac{n}{n+1}\right)^{n+\frac{1}{2}}$

→ [voir détail 1A niveau T+, pour le calcul détaillé]

Donc :

$\ln\left(\frac{u_{n+1}}{u_{n}}\right)=1-\left(n+\frac{1}{2}\right)\ln\left(1+\frac{1}{n}\right)$

En utilisant le développement limité de $t\mapsto\ln\left(1+t\right)$ au voisinage de $0$ à l’ordre $3,$ on constate que :

$\ln\left(\frac{u_{n+1}}{u_{n}}\right)=1-\left(n+\frac{1}{2}\right)\left(\frac{1}{n}-\frac{1}{2n^{2}}+\frac{1}{3n^{3}}+o\left(\frac{1}{n^{3}}\right)\right)$

c’est-à-dire :

$\boxed{\ln\left(\frac{u_{n+1}}{u_{n}}\right)\sim-\frac{1}{12n^{2}}}$

Ceci prouve, comme souhaité, que la série $\sum_{n\geqslant1}\ln\left(\frac{u_{n+1}}{u_{n}}\right)$ converge, et donc que la suite $\left(u_{n}\right)_{n\geqslant1}$ converge vers une limite non nulle, que nous notons $\lambda.$

Détail étape 2 (niveau Sup) (cliquer pour déplier / replier)

En combinant les résultats établis à la section 3 et à la section 4, on obtient l’équivalent suivant (lorsque $p$ tend vers $+\infty$ ) :

$\frac{\left(2p\right)!\thinspace\pi}{2^{2p+1}\left(p!\right)^{2}}\sim\frac{1}{2}\sqrt{\frac{\pi}{p}}\qquad\clubsuit$

Par ailleurs, vu que $\lambda\neq0,$ la convergence de la suite $\left(u_{n}\right)_{n\geqslant1}$ vers $\lambda$ peut s’écrire :

$n!\sim\lambda\left(\frac{n}{e}\right)^{n}\sqrt{n}$

En injectant cette dernière relation dans $\left(\clubsuit\right),$ on trouve :

$\frac{\lambda\left(\frac{2p}{e}\right)^{2p}\sqrt{2p}\pi}{2^{2p+1}\left(\lambda\left(\frac{p}{e}\right)^{p}\sqrt{p}\right)^{2}}\sim\frac{1}{2}\sqrt{\frac{\pi}{p}}$