Neuf énoncés d’exercices sur les équations du second degré (fiche 01).
Considérons une équation du second degré :
![Rendered by QuickLaTeX.com \[ax^2+bx+c=0\qquad a,b,c\in\mathbb{R}\text{ et }a\neq0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-48b6b3e24172225309ffde0a6e17fed9_l3.png)
Sa résolution (dans
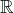
) est mécanique avec la
« Recette du discriminant » :
- On calcule le discriminant
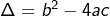 , puis on examine son signe
, puis on examine son signe
- Trois cas se présentent :
Bien sûr, il faut connaître cette recette ! Mais il est important de s’assurer que l’on comprend véritablement ce qui la sous-tend.
Pour cela, on peut s’entraîner à résoudre quelques équations du second degré en évitant de se servir du discriminant, mais en mettant plutôt le trinôme sous forme canonique, puis en le factorisant (si c’est possible).
En outre, il est assez malvenu de faire intervenir le discriminant dans les cas suivants :
- pour une équation de la forme
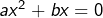 (on met
(on met 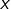 en facteur …)
en facteur …)
- pour une équation de la forme
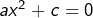 , car (en supposant
, car (en supposant 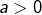 , ce qui ne diminue en rien la généralité, quitte à multiplier les deux membres de l’équation par -1) :
, ce qui ne diminue en rien la généralité, quitte à multiplier les deux membres de l’équation par -1) :
L’expression développée de 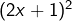 est
est 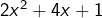 .
.
Ce calcul est faux ! Où est l’erreur ?
Quelle est l’erreur dans le calcul suivant ?
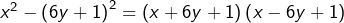
En quoi la résolution suivante est-elle incorrecte ?
Pour résoudre 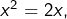 on simplifie par
on simplifie par 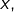 ce qui donne immédiatement
ce qui donne immédiatement 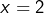 .
.
La seule solution est donc 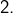
Résoudre chacune des équations suivantes, sans utiliser la recette du discriminant :
![Rendered by QuickLaTeX.com \[\begin{matrix}x^{2}-4x=0 & ; & 10x-x^{2}=5x^{2}+x & ; & x^{2}-1=0\\\\\left(x+1\right)^{2}=9 & ; & \left(2x+3\right)^{2}=\left(x-4\right)^{2} & ; & 7x^{2}+1=0\end{matrix}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b2d9b9fb81c1fa12a8dca79fc8d0bd7a_l3.png)
Même consigne pour :
![Rendered by QuickLaTeX.com \[\begin{matrix}x^{2}+2x+1=0 & ; & 6x-x^{2}=9 & ; & 4x^{2}+4x=1\\\\5x\left(x+1\right)=\left(x+1\right)\left(x+2\right) & ; & \left(x+3\right)^{2}+\left(x-3\right)^{2}=12x & ; & 18x^{2}-48x+32=0\end{matrix}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-51000ac41cd8bd3f369ed73233029588_l3.png)
Même consigne pour :
![Rendered by QuickLaTeX.com \[\begin{matrix}x^{2}+2x-3=0 & ; & 4x^{2}+x+1=0 & ; & 2x^{2}-5x+2=0\\\\\left(x-2\right)^{2}=x & ; & 3x^{2}-1=4\left(x+\frac{1}{2}\right)^{2} & ; & \left(x+1\right)^{2}+\left(x+2\right)^{2}=x+3\\\\3x^{2}+2x-1=0 & ; & 7x^{2}+6x=2 & ; & \frac{x^{2}}{7}+\frac{x}{6}-\frac{1}{5}=0\end{matrix}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a009e78c1d7ef2e116cbb4cbe0a43fbc_l3.png)
Les équations suivantes ne sont pas du second degré, mais elle s’y ramènent.
Il s’agit de résoudre chacune d’elles.
![Rendered by QuickLaTeX.com \[\begin{matrix}{\displaystyle \frac{1}{x}+\frac{1}{x+1}=\frac{1}{x+3}} & ; & \frac{x}{2+\frac{1}{x-1}}=1-x & ; & x^{2}-5\left|x\right|+6=0\\\\\left(x^{2}-1\right)^{2}=9 & ; & 5x-7\sqrt{x}-12=0 & ; & x^{6}-16x^{3}+64=0\end{matrix}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3bb0e5c1d612a66868a5abce46a753fa_l3.png)
Comment choisir le réel 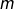 pour que l’équation
pour que l’équation
![Rendered by QuickLaTeX.com \[ \left(m-1\right)x^{2}+\left(2m+1\right)x-1=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0df600ada0b71277d8751edd3a2c71f4_l3.png)
(d’inconnue
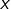
) possède une unique solution réelle ?
Soient 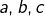 trois nombres réels (avec
trois nombres réels (avec 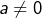 ). On suppose que l’équation
). On suppose que l’équation 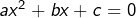 possède deux solutions distinctes, notées
possède deux solutions distinctes, notées 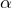 et
et 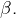 On note
On note 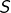 leur somme et
leur somme et 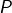 leur produit.
leur produit.
Pour tout 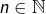 , on note
, on note 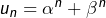 .
.
Trouver une formule de récurrence vérifiée par la suite 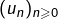 .
.
Calculer, en fonction de 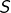 et
et 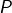 , les nombres
, les nombres 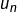 pour
pour 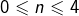 .
.
Cliquer ici pour accéder aux indications
Cliquer ici pour accéder aux solutions
J’aime ça :
J’aime chargement…
![]()
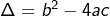 , puis on examine son signe
, puis on examine son signe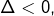 l’équation ne possède aucune solution
l’équation ne possède aucune solution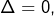 l’équation possède une solution unique :
l’équation possède une solution unique :![Rendered by QuickLaTeX.com \[-\frac{b}{2a}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5e5de42f41b58de58cde6b24f32e81fb_l3.png)
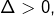 l’équation possède deux solutions :
l’équation possède deux solutions :![Rendered by QuickLaTeX.com \[\frac{-b-\sqrt{\Delta}}{2a}\qquad\text{et}\qquad\frac{-b+\sqrt{\Delta}}{2a}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4b02cdcb97a0066b1c40d907d536a64e_l3.png)
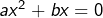 (on met
(on met 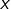 en facteur …)
en facteur …)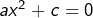 , car (en supposant
, car (en supposant 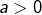 , ce qui ne diminue en rien la généralité, quitte à multiplier les deux membres de l’équation par -1) :
, ce qui ne diminue en rien la généralité, quitte à multiplier les deux membres de l’équation par -1) :
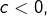 on reconnaît une différence de deux carrés, que l’on factorise,
on reconnaît une différence de deux carrés, que l’on factorise,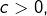 on justifie l’absence de solutions par le fait que
on justifie l’absence de solutions par le fait que![Rendered by QuickLaTeX.com \[\forall x\in\mathbb{R},\,ax^2+c\geqslant c\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0393db7d9b986f78a4a75f352da37641_l3.png)
![Rendered by QuickLaTeX.com \[\forall x\in\mathbb{R},\,ax^2+c\neq0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-81014a598fbe85a4bda7882bdaa32585_l3.png)
![Rendered by QuickLaTeX.com \[\begin{matrix}x^{2}-4x=0 & ; & 10x-x^{2}=5x^{2}+x & ; & x^{2}-1=0\\\\\left(x+1\right)^{2}=9 & ; & \left(2x+3\right)^{2}=\left(x-4\right)^{2} & ; & 7x^{2}+1=0\end{matrix}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b2d9b9fb81c1fa12a8dca79fc8d0bd7a_l3.png)
![Rendered by QuickLaTeX.com \[\begin{matrix}x^{2}+2x+1=0 & ; & 6x-x^{2}=9 & ; & 4x^{2}+4x=1\\\\5x\left(x+1\right)=\left(x+1\right)\left(x+2\right) & ; & \left(x+3\right)^{2}+\left(x-3\right)^{2}=12x & ; & 18x^{2}-48x+32=0\end{matrix}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-51000ac41cd8bd3f369ed73233029588_l3.png)
![Rendered by QuickLaTeX.com \[\begin{matrix}x^{2}+2x-3=0 & ; & 4x^{2}+x+1=0 & ; & 2x^{2}-5x+2=0\\\\\left(x-2\right)^{2}=x & ; & 3x^{2}-1=4\left(x+\frac{1}{2}\right)^{2} & ; & \left(x+1\right)^{2}+\left(x+2\right)^{2}=x+3\\\\3x^{2}+2x-1=0 & ; & 7x^{2}+6x=2 & ; & \frac{x^{2}}{7}+\frac{x}{6}-\frac{1}{5}=0\end{matrix}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a009e78c1d7ef2e116cbb4cbe0a43fbc_l3.png)
![Rendered by QuickLaTeX.com \[\begin{matrix}{\displaystyle \frac{1}{x}+\frac{1}{x+1}=\frac{1}{x+3}} & ; & \frac{x}{2+\frac{1}{x-1}}=1-x & ; & x^{2}-5\left|x\right|+6=0\\\\\left(x^{2}-1\right)^{2}=9 & ; & 5x-7\sqrt{x}-12=0 & ; & x^{6}-16x^{3}+64=0\end{matrix}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3bb0e5c1d612a66868a5abce46a753fa_l3.png)
![]()