Neuf énoncés d’exercices sur l’uniforme continuité (fiche 01).
Deux exercices corrigés sur ce thème sont consultables ici

A tout ![]() on associe l’application
on associe l’application ![]()
Pour quelles valeurs de ![]() cette application est-elle uniformément continue ?
cette application est-elle uniformément continue ?

Les applications
![]()
![]()

Soit ![]() un intervalle non trivial de
un intervalle non trivial de ![]() et soient
et soient ![]() deux applications uniformément continues. Montrer que
deux applications uniformément continues. Montrer que ![]() est aussi uniformément continue.
est aussi uniformément continue.
Peut-on en dire autant de ![]() ? Et si
? Et si ![]() et
et ![]() sont de plus supposées bornées ?
sont de plus supposées bornées ?

Soit ![]() un intervalle non trivial de
un intervalle non trivial de ![]() soit
soit ![]() une suite d’applications uniformément continues de
une suite d’applications uniformément continues de ![]() dans
dans ![]() qui converge uniformément sur
qui converge uniformément sur ![]() vers
vers ![]() Montrer que
Montrer que ![]() est uniformément continue.
est uniformément continue.

Montrer que si ![]() est continue et périodique, alors
est continue et périodique, alors ![]() est uniformément continue.
est uniformément continue.

Soient ![]() tels que
tels que ![]() et soit
et soit ![]() uniformément continue. Montrer que
uniformément continue. Montrer que ![]() est bornée. Reprendre alors le premier exemple de l’exercice 2.
est bornée. Reprendre alors le premier exemple de l’exercice 2.

Soient ![]() continues et
continues et ![]() Calculer :
Calculer :
![Rendered by QuickLaTeX.com \[ \lim_{n\rightarrow+\infty}\,\frac{1}{n}\,\sum_{k=0}^{n-1}\,f\left(\frac{k}{n}\right)\,g\left(\frac{k}{n}+\frac{1}{n^{\alpha}}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-dd9601a7485504095da1dc7c27e09250_l3.png)

On suppose (hypothèse (H)) que :
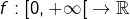 continue
continue- l’intégrale impropre
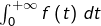 converge.
converge.
- Montrer que si
 admet en
admet en 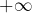 une limite, alors celle-ci est nécessairement nulle.
une limite, alors celle-ci est nécessairement nulle. - Montrer par un exemple que (H) n’entraîne pas
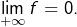
- Montrer que si l’on ajoute à (H) l’hypothèse d’uniforme continuité de
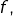 alors
alors 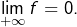

Soit ![]() continue. On pose pour tout
continue. On pose pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[ I_{n}=\sum_{k=0}^{n-1}\left|\int_{x_{k,n}}^{x_{k+1,n}}f\left(t\right)\thinspace dt\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b1c1c45084a17a8bcb8531a8e6f32db6_l3.png)
avec ![]() pour tout
pour tout ![]()
Calculer ![]()
Cliquer ici pour accéder aux indications
Cliquer ici pour accéder aux solutions

