

Supposons ![]() A tout réel
A tout réel ![]() associons le réel
associons le réel
![]()
D’une part :
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}p_{\alpha}\left(x'\right)-p_{\alpha}\left(x\right) & = & \left(x+\frac{1}{x^{\alpha-1}}\right)^{\alpha}-x^{\alpha}\\& = & x^{\alpha}\left[\left(1+\frac{1}{x^{\alpha}}\right)^{\alpha}-1\right]\\& \underset{x\rightarrow+\infty}{\rightarrow} & \alpha\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-334b570a87909780929767ba9d82359f_l3.png)
Par conséquent, si l’on choisit ![]() on voit que pour tout
on voit que pour tout ![]() on peut trouver un couple
on peut trouver un couple ![]() vérifiant :
vérifiant :
![Rendered by QuickLaTeX.com \[ \left\{\begin{array}{c}\vert x'-x\vert\leqslant\delta\\\\\left|p_{\alpha}\left(x'\right)-p_{\alpha}\left(x\right)|>\epsilon\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9f72dd23e74b861ec84e9e9c7c1bf081_l3.png)
Ainsi, ![]() n’est pas UC lorsque
n’est pas UC lorsque ![]()
Supposons maintenant ![]() La restriction de
La restriction de ![]() à
à ![]() est UC d’après le théorème de Heine. De plus, pour tout
est UC d’après le théorème de Heine. De plus, pour tout ![]() tel que
tel que ![]() il existe (d’après la formule des accroissements finis)
il existe (d’après la formule des accroissements finis) ![]() tel que :
tel que :
![]()
![]()
Ainsi, la restriction de ![]() à
à ![]() est lipschitzienne, donc UC elle aussi.
est lipschitzienne, donc UC elle aussi.
Par conséquent, ![]() est UC.
est UC.
Quant au cas ![]() il est évident. En conclusion :
il est évident. En conclusion :
![]()

En choisissant ![]() on voit que pour tout
on voit que pour tout ![]() on peut trouver
on peut trouver ![]() vérifiant :
vérifiant :
![]()
Il suffit en effet de considérer ![]() et
et ![]() (puisque
(puisque ![]() Par conséquent :
Par conséquent :
![]()
Passons à l’application ![]()
L’allure de son graphe suggère de considérer les couples formés d’un minimum local et du maximum local suivant : l’écart des abscisses sera arbitrairement petit tandis que l’écart des ordonnées sera fixe.
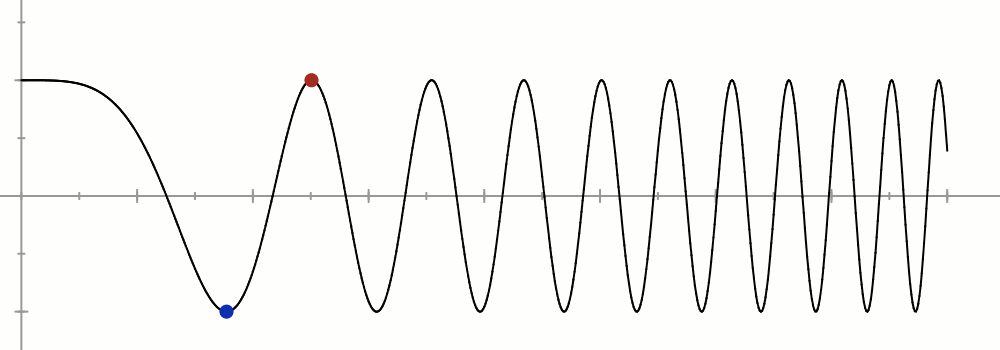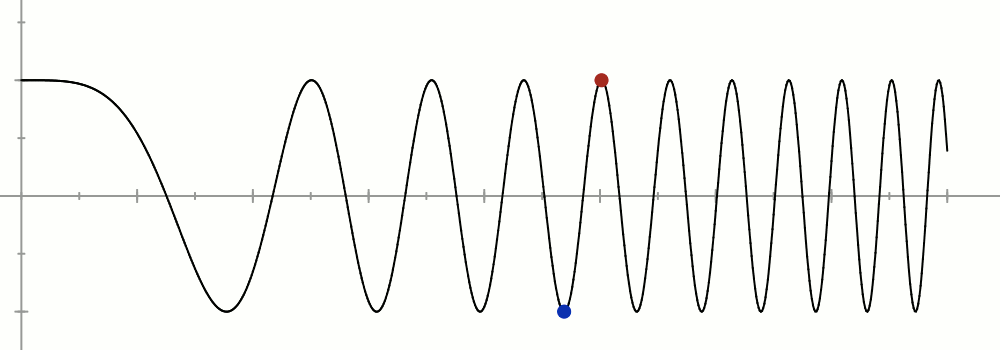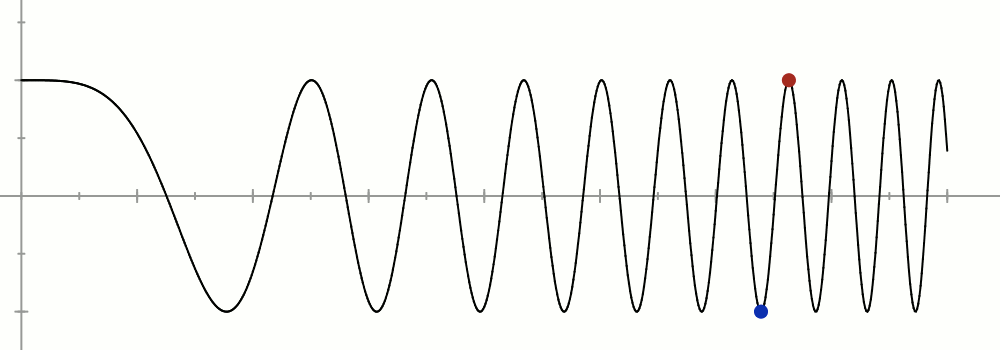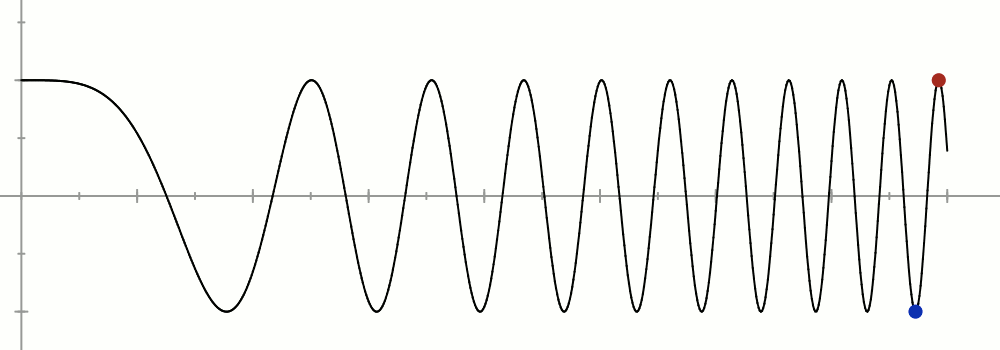
Posons donc, pour tout ![]() :
:
![]()
![]()
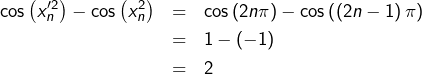
En choisissant ![]() on peut donc trouver, pour tout
on peut donc trouver, pour tout ![]() un couple
un couple ![]() tel que :
tel que :
![]()
![]()

Montrons que ![]() est uniformément continue.
est uniformément continue.
Soit ![]() Comme
Comme ![]() est UC, il existe
est UC, il existe ![]() tel que :
tel que :
![]()
De même, il existe ![]() tel que :
tel que :
![]()
Posons ![]() Grâce à l’inégalité triangulaire, on voit que si
Grâce à l’inégalité triangulaire, on voit que si ![]() vérifie
vérifie ![]() alors :
alors :
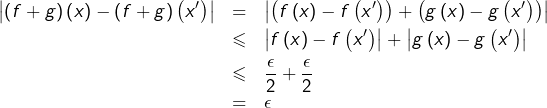
Pour le produit, c’est différent. Par exemple, si ![]() alors
alors ![]() est l’application
est l’application ![]() qui n’est pas UC, bien que
qui n’est pas UC, bien que ![]() et
et ![]() le soient.
le soient.
Considérons maintenant un couple ![]() d’applications UC et bornées de
d’applications UC et bornées de ![]() dans
dans ![]() .
.
Notons ![]() deux réels strictement positfs tels que :
deux réels strictement positfs tels que :
![]()
On observe que, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \begin{eqnarray*}\left|\left(fg\right)\left(x\right)-\left(fg\right)\left(x'\right)\right| & = & \left|f\left(x\right)g\left(x\right)-f\left(x'\right)g\left(x'\right)\right|\\& = & \left|f\left(x\right)\left[g\left(x\right)-g\left(x'\right)\right]+\left[f\left(x\right)-f\left(x'\right)\right]g\left(x'\right)\right|\\& \leqslant & A\left|g\left(x\right)-g\left(x'\right)\right|+B\left|f\left(x\right)-f\left(x'\right)\right| \end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-ceb33a0d069c7e151f30043a606e05be_l3.png)
Etant donné ![]() il existe
il existe ![]() et
et ![]() tels que pour tout
tels que pour tout ![]() :
:
![]()
![]()
On voit maintenant que :
![]()
Proposition
Le produit de deux applications UC et bornées est UC

Soit ![]() On peut artificiellement écrire, pour tout
On peut artificiellement écrire, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \begin{eqnarray*}\left|g\left(x\right)-g\left(x'\right)\right| & = & \left|\left[g\left(x\right)-f_{n}\left(x\right)\right]+\left[f_{n}\left(x\right)-f_{n}\left(x'\right)\right]+\left[f_{n}\left(x'\right)-g\left(x'\right)\right]\right|\\& \leqslant & \left|g\left(x\right)-f_{n}\left(x\right)\right|+\left|f_{n}\left(x\right)-f_{n}\left(x'\right)\right|+\left|f_{n}\left(x'\right)-g\left(x'\right)\right|\\& \leqslant & 2\left\Vert g-f_{n}\right\Vert_{\infty}+\left|f_{n}\left(x\right)-f_{n}\left(x'\right)\right|\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-4e751aa99f5d2a6b15666914850866c5_l3.png)
Etant donné ![]() on commence par choisir
on commence par choisir ![]() assez grand pour que :
assez grand pour que :
![]()
![]()
Au final, on voit que pour tout ![]() :
:
![]()
Proposition
Pour toute suite uniformément convergente d’applications UC, la limite est UC.

Soit ![]() une période de
une période de ![]() Le théorème de Heine assure l’uniforme continuité de
Le théorème de Heine assure l’uniforme continuité de ![]() sur
sur ![]() Donc, étant donné
Donc, étant donné ![]() il existe
il existe ![]() tel que :
tel que :
![]()
Imposons en outre ![]() (c’est possible, quitte à remplacer
(c’est possible, quitte à remplacer ![]() par
par ![]()
Soient ![]() vérifiant
vérifiant ![]()
Supposons, sans perte de généralité, que ![]() et notons
et notons ![]()
Alors : ![]() et
et
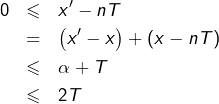
Ainsi ![]() et
et ![]() donc :
donc :
![]()
Proposition
Toute application continue et périodique est UC.

Soit ![]() Il existe par hypothèse
Il existe par hypothèse ![]() tel que :
tel que :
![]()
En particulier, on voit que si ![]() et
et ![]() appartiennent tous deux à
appartiennent tous deux à ![]() alors
alors ![]()
Autrement dit, ![]() vérifie le critère de Cauchy au point
vérifie le critère de Cauchy au point ![]() Comme
Comme ![]() est complet, il en résulte que
est complet, il en résulte que ![]() admet en
admet en ![]() une limite finie.
une limite finie.
Bien entendu, la situation est analogue en ![]()
On peut donc prolonger ![]() en une application continue
en une application continue ![]()
Mais on sait que tout application continue sur un segment, à valeurs réelles, est bornée.
En conséquence, ![]() est bornée.
est bornée.
Dans l’exercice 2, on a vu directement que l’application ![]() n’est pas uniformément continue. On peut voir cela comme conséquence du résultat précédent. En effet, si
n’est pas uniformément continue. On peut voir cela comme conséquence du résultat précédent. En effet, si ![]() était UC alors sa restriction à
était UC alors sa restriction à ![]() serait UC donc bornée : contradiction !
serait UC donc bornée : contradiction !
Posons, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[S_{n}=\frac{1}{n}\,\sum_{k=0}^{n-1}\,f\left(\frac{k}{n}\right)\,g\left(\frac{k}{n}+\frac{1}{n^{\alpha}}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ae948f40abb399d7f049fa3542d2dac2_l3.png)
![Rendered by QuickLaTeX.com \[T_{n}=\frac{1}{n}\,\sum_{k=0}^{n-1}\,f\left(\frac{k}{n}\right)\,g\left(\frac{k}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e542134d597e95c7d502c614683d555f_l3.png)
Détail (cliquer pour déplier / replier)
Pour que la somme qui définit ![]() ait un sens, encore faut-il que les réels auxquels
ait un sens, encore faut-il que les réels auxquels ![]() est appliquée soient tous dans
est appliquée soient tous dans ![]()
Et c’est bien le cas, parce qu’on a supposé ![]() ce qui entraîne :
ce qui entraîne :
![]()
On sait (théorème de convergence des sommes de Riemann) que :
![]()
Il suffit donc de montrer que :
![]()
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow+\infty}\,\frac{1}{n}\,\sum_{k=0}^{n-1}\,f\left(\frac{k}{n}\right)\,g\left(\frac{k}{n}+\frac{1}{n^{\alpha}}\right)=\int_{0}^{1}\,f\left(t\right)\,g\left(t\right)\,dt}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5b94ee155eca44a6cc40ede5fdc498c1_l3.png)
Or, d’après inégalité triangulaire :
![Rendered by QuickLaTeX.com \begin{eqnarray*}\left|S_{n}-T_{n}\right| & = & \frac{1}{n}\,\left|\sum_{k=1}^{n}\,f\left(\frac{k}{n}\right)\left[g\left(\frac{k}{n}+\frac{1}{n^{\alpha}}\right)-g\left(\frac{k}{n}\right)\right]\right|\\& \leqslant & \frac{1}{n}\,\sum_{k=1}^{n}\,\left|f\left(\frac{k}{n}\right)\right|\,\left|g\left(\frac{k}{n}+\frac{1}{n^{\alpha}}\right)-g\left(\frac{k}{n}\right)\right|\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-8a6c1cc7bb878b713b9930bb4a40b4d6_l3.png)
Etant donné
![]()
![Rendered by QuickLaTeX.com \[ n\geqslant{\displaystyle \left(\frac{1}{\delta}\right)^{1/\alpha}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2a7e490c3758f3e151f6cad4d1ec5ff1_l3.png)
![Rendered by QuickLaTeX.com \[\left|S_{n}-T_{n}\right|\leqslant\frac{\varepsilon}{n}\,\sum_{k=1}^{n}\,\left|f\left(\frac{k}{n}\right)\right|\leqslant\varepsilon\left\Vert f\right\Vert _{\infty}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e9950b1bda1c12815f025d204d3a2a3d_l3.png)

Question 1
Supposons (H) remplie et supposons de plus que ![]() admette en
admette en ![]() une limite, finie ou non.
une limite, finie ou non.
Dans un premier temps, supposons qu’il s’agisse d’une limite finie ![]() Il existe alors un réel
Il existe alors un réel ![]() tel que :
tel que :
![]()
![]()
![]()
Il s’ensuit que :
![]()
En remplaçant ![]() par
par ![]() on voit que
on voit que ![]() ne peut pas non plus être strictement négative.
ne peut pas non plus être strictement négative.
Et en adaptant très légèrement ce qui précède, on voit que ![]() ne peut pas non posséder en
ne peut pas non posséder en ![]() une limite infinie. Ainsi, il est nécessaire que la limite
une limite infinie. Ainsi, il est nécessaire que la limite ![]() soit nulle.
soit nulle.
Question 2
Dans l’illustration ci-dessous, les triangles coloriés en bleu ont pour aires respectives :
![]()
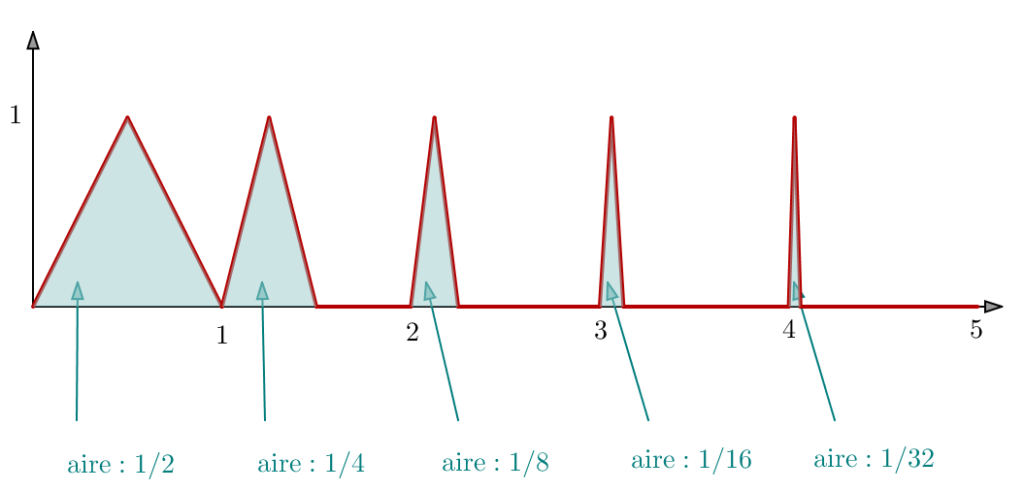
Transformons cette idée en une preuve rigoureuse, en posant pour tout ![]() et tout
et tout ![]() :
:
![Rendered by QuickLaTeX.com \[f\left(t\right)=\left\{\begin{array}{ccc}2^{n}\left(t-n+1\right) & \text{si} & t-n+1\in\left[0,2^{-n}\right[\\\\-2^{n}\left(t-n+1-2^{-n}\right) & \text{si} & t-n+1\in\left[2^{-n},2^{1-n}\right[\\\\0 & \text{si} & t-n+1\in\left[2^{1-n},1\right[\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cbb653ec64c1e7591a56c253a2819e81_l3.png)
On définit ainsi une application ![]() par ses restrictions aux intervalles
par ses restrictions aux intervalles ![]() pour
pour ![]()
Il sera peut-être plus clair de reformuler comme suit. Pour tout entier ![]() :
:
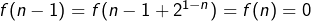 ,
,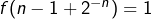
- la restriction de
 à chacun des segments
à chacun des segments ![Rendered by QuickLaTeX.com \left[n-1,n-1+2^{-n}\right],](https://math-os.com/wp-content/ql-cache/quicklatex.com-2131643a4ecb56ed5c0704bc3818c689_l3.png)
![Rendered by QuickLaTeX.com \left[n-1+2^{-n},\thinspace n-1+2^{1-n}\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ec75234642d1a306e911ee2a73fa6a5a_l3.png) et
et ![Rendered by QuickLaTeX.com \left[n-1+2^{1-n},1\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1396a5e740feef301a2d2d43c8bae844_l3.png) est affine.
est affine.
L’hypothèse (H) est vérifiée puisque, d’une part, ![]() est continue (par construction) et, d’autre part, pour tout
est continue (par construction) et, d’autre part, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\int_{0}^{x}f\left(t\right)\thinspace dt\leqslant\int_{0}^{\left\lceil x\right\rceil }f\left(t\right)\thinspace dt=\sum_{k=0}^{\left\lceil x\right\rceil -1}2^{-k}<1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-af544473e623e9cc677ff4382ae94a1b_l3.png)
Pourtant, ![]() n’admet pas de limite en
n’admet pas de limite en ![]() puisqu’en posant
puisqu’en posant
![Rendered by QuickLaTeX.com \[\left\{\begin{array}{ccc}t_{n} & = & n-1\\\\t'_{n} & = & n-1+2^{-n}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8eeca3f9eed2da1f68c9cc18078daf86_l3.png)
![]()
![]()
Question 3
Supposons que ![]() n’admette pas pour limite
n’admette pas pour limite ![]() en
en ![]() :
:
![]()
On peut alors construire (par récurrence) une suite ![]() strictement croissante telle que :
strictement croissante telle que :
![Rendered by QuickLaTeX.com \[\left\{\begin{array}{c} {\displaystyle \lim_{n\rightarrow\infty}\,x_{n}=+\infty}\\\\\forall n\in\mathbb{N},\,\left|f\left(x_{n}\right)\right|\geqslant2\varepsilon\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5b538001ff0995652d78ccb3380cdada_l3.png)
Détail (cliquer pour déplier / replier)
La condition ![]() garantit que les segments
garantit que les segments ![]() qui apparaissent ci-après sont tous contenus dans
qui apparaissent ci-après sont tous contenus dans ![]() ce qui va permettre d’appliquer
ce qui va permettre d’appliquer ![]() à leurs éléments.
à leurs éléments.
Comme ![]() est uniformément continue, il existe
est uniformément continue, il existe ![]() tel que :
tel que :
![]()
![]()
![]()
D’après la théorème des valeurs intermédiaires, ![]() garde un signe constant sur chacun des segments
garde un signe constant sur chacun des segments ![]() Donc, pour tout
Donc, pour tout ![]() :
:
![]()

Rappelons que ![]() est supposée continue et qu’on a posé, pour tout
est supposée continue et qu’on a posé, pour tout ![]() et tout
et tout ![]() :
:
![]()
Pour tout tel couple ![]() , il existe (d’après la formule de la moyenne) un réel
, il existe (d’après la formule de la moyenne) un réel
![]()
![]()
![Rendered by QuickLaTeX.com \[S_{n}=\frac{b-a}{n}\sum_{k=0}^{n-1}\left|f\left(x_{k,n}\right)\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-caa61283bfe5ce2b39a460d74c2894e2_l3.png)
![]()
Par inégalité triangulaire, pour tout ![]() :
:
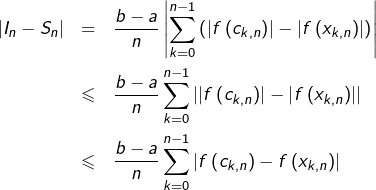
![]() étant UC (théorème de Heine), il existe pour tout
étant UC (théorème de Heine), il existe pour tout ![]() un réel
un réel ![]() tel que :
tel que :
![]()
Ainsi :
![]()
On a prouvé que :
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow\infty}I_{n}=\int_{a}^{b}\left|f\left(t\right)\right|\thinspace dt}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ec1bf2d2e2785eb93f0308c969e60ab4_l3.png)
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
