Exercices de calcul de sommes – 03

Neuf énoncés d’exercices sur les calculs de sommes (fiche 03).

icone-math-OS-Exos
exercice 1 facile

Soit \left(u_{n}\right)_{n\geqslant0} une suite arithmétique de raison r\in\mathbb{C}.

Montrer que si p,q\in\mathbb{N} sont tels que p\leqslant q, alors :

    \[\sum_{k=p}^{q}u_{k}=\frac{\left(q-p+1\right)\left(u_{p}+u_{q}\right)}{2}\]

exercice 2 facile

Calculer :

    \[\lim_{n\rightarrow\infty}\prod_{k=2}^{n}\frac{\ln(k)}{1+\ln(k)}\]

Soient \left(t_{n}\right)_{n\geqslant1} une suite de nombres réels et \left(z_{n}\right)_{n\geqslant1} une suite de nombres complexes.

On pose pour tout n\geqslant1 :

    \[S_{n}=\sum_{k=1}^{n}z_{k}\]

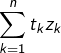Exprimer {\displaystyle \sum_{k=1}^{n}t_{k}z_{k}} au moyen de t_1,\ldots,t_n et de S_1,\ldots,S_n.

En déduire que si la suite \left(t_{n}\right)_{n\geqslant1} décroît et converge vers 0 et si de plus la suite \left(S_{n}\right)_{n\geqslant1} est bornée, alors la série {\displaystyle \sum_{k\geqslant1}t_{k}z_{k}} converge.

Etant donnés n\in\mathbb{N}^{\star} et \theta\in\mathbb{R}-2\pi\mathbb{Z}, calculer explicitement la somme :

    \[B_{n}\left(\theta\right)=\sum_{k=1}^{n}\sin\left(k\theta\right)\]

en considérant qu’il s’agit de la partie imaginaire d’une certaine somme géométrique.

Retrouver ce résultat en examinant l’expression \displaystyle{\sin\left(\frac{\theta}{2}\right)B_{n}\left(\theta\right)} et en faisant apparaître une sommation télescopique.

Calculer plus simplement , pour tout entier n\geqslant2 :

    \[S_{n}=\sum_{k=1}^{n}\binom{n}{k-1}\binom{n}{k}\]

On tâchera de privilégier un point de vue combinatoire.

Etant donné n\geqslant2 et \omega=e^{2i\pi/n}, on considère la matrice M=\left[\omega^{\left(p-1\right)\left(q-1\right)}\right]_{1\leqslant p,q\leqslant n}\in\mathcal{M}_{n}\left(\mathbb{C}\right).

Calculer M\overline{M} ainsi que M^{2}.

On pose, pour tout entier n\geqslant2 :

    \[u_{n}=\sum_{k=1}^{n-1}\frac{1}{k^{2}\left(n-k\right)^{2}}\]

Exprimer u_{n} au moyen des sommes :

    \[S_{n}=\sum_{k=1}^{n-1}\frac{1}{k^{2}}\qquad\text{et}\qquad H_{n}=\sum_{k=1}^{n-1}\frac{1}{k}\]

En déduire la nature de la série {\displaystyle \sum_{n\geqslant2}u_{n}.}

On pose pour tout entier n\geqslant2 :

    \[p_{n}=\prod_{k=1}^{n-1}\sin\left(\frac{k\pi}{n}\right)\]

Calculer p_{n} explicitement.

En déduire le calcul de l’intégrale impropre {\displaystyle \int_{0}^{\pi/2}\ln\left(\sin\left(t\right)\right)\thinspace dt,} après avoir justifié sa convergence.

exercice 9 difficile

Montrer que pour tout \left(x,y\right)\in\mathbb{R}^{2} et pour tout n\in\mathbb{N}^{\star} :

    \[\left(x+y\right)^{n}=x^{n}+\sum_{k=1}^{n}\binom{n}{k}y\left(y-k\right)^{k-1}\left(x+k\right)^{n-k}\]

Cliquer ici pour accéder aux indications
Cliquer ici pour accéder aux solutions

Partager cet article
    
Étiquettes : , , , , , ,

Laisser un commentaire