Indications - Exercices de calcul de sommes - 03

Indications pour démarrer les exercices sur les calculs de sommes (fiche 03).
Cliquer ici pour accéder aux énoncés.

On peut calculer le double de la somme demandée en associant le premier terme au dernier, le second à l’avant-dernier, etc …

L’application

$\left[0,+\infty\right[\rightarrow\mathbb{R},t\thinspace\mapsto\frac{t}{1+t}$

est croissante. Ceci devrait permettre de majorer le produit par une expression plus simple.

Pour le première question, observer que pour tout $k\in\mathbb{N}^{\star}$ :

$z_{k}=S_{k}-S_{k-1}$

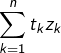(à condition de poser $S_{0}=0).$ Pour la seconde question, on peut transformer la somme partielle $\sum_{k=1}^{n}t_{k}z_{k}$ et faire apparaître la $n-$ ème somme partielle d’une série absolument convergente.

Il semble bien que l’énoncé donne déjà suffisamment d’indications …

Imaginer un ensemble $E$ de cardinal $2n$ dans lequel on prélèverait un sous-ensemble de cardinal $n-1.$ On peut cloisonner $E$ en deux parties disjointes et de même cardinal …

On applique la formule qui donne l’expression du produit de deux matrices. Des sommes géométriques doivent apparaître … Attention : les indices de ligne et de colonne sont notés $p,q$ (et non pas $i,j$ afin d’éviter toute collision avec le nombre complexe $i$ ).

On peut chercher à exprimer

$\frac{n^{2}}{k^{2}\left(n-k\right)^{2}}$

comme la somme de trois fractions plus simples, ce qui ramènera le calcul de $u_{n}$ à des sommations classiques. On peut aussi (plus rapide mais plus « savant ») reconnaître qu’il s’agit d’un produit de Cauchy.

En utilisant la formule d’Euler pour le sinus :

$\forall t\in\mathbb{R},\thinspace\sin\left(t\right)=\frac{e^{it}-e^{-it}}{2i}$

on peut ré-écrire le produit $p_{n}$ sous une forme plus maniable; on fait notamment apparaître la valeur en 1 du polynôme :

$Q_{n}=\prod_{k=1}^{n-1}\left(X-e^{2ik\pi/n}\right)$

Comparer les dérivées par rapport à $x$ de chaque membre et raisonner par récurrence.

Partager cet article