Solutions détaillées de neuf exercices sur les calculs de sommes (fiche 03).
Cliquer ici pour accéder aux énoncés.
Considérons une suite arithmétique 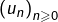 de raison
de raison  .
.
Pour 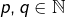 tels que
tels que 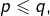 notons :
notons :
![Rendered by QuickLaTeX.com \[ S_{p,q}=\sum_{k=p}^{q}u_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cd36fbccd6156d9ad8dcd47d7e6d7de1_l3.png)
Alors :
![Rendered by QuickLaTeX.com \[2\thinspace S_{p,q}=\sum_{k=p}^{q}\left(u_{k}+u_{q+p-k}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5e86102a92306b1cd9b7289952831174_l3.png)
Or, pour tout
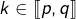
:
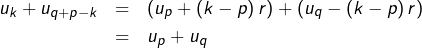
et donc :
![Rendered by QuickLaTeX.com \[2\thinspace S_{p,q}=\left(q-p+1\right)\left(u_{p}+u_{q}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-26bd0f4649071b60b13d79de212b9a02_l3.png)
d’où la conclusion. Il est conseillé de mémoriser ce résultat, sous la forme :
Proposition
La valeur d’une somme arithmétique s’obtient en effectuant l’opération suivante :
![Rendered by QuickLaTeX.com \[\frac{\left(\left(\text{premier terme}\right)+\left(\text{dernier terme}\right)\right)\times\left(\text{nb de termes}\right)}{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-163e144c65ec961a2a274caea4f82b5e_l3.png)
L’application
![Rendered by QuickLaTeX.com \[f:\left[0,+\infty\right[\rightarrow\mathbb{R},\thinspace t\mapsto\frac{t}{1+t}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c09e4e3675047d69f41ba39cbecfcbb1_l3.png)
est croissante, puisque sa dérivée est donnée par :
![Rendered by QuickLaTeX.com \[\forall t\geqslant0,\thinspace f'\left(t\right)=\frac{1}{\left(1+t\right)^{2}}>0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a39a15f8c85188d2b6b6bac839117a46_l3.png)
Par ailleurs, on sait que 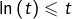 pour tout
pour tout 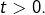 Par conséquent :
Par conséquent :
![Rendered by QuickLaTeX.com \[\forall k\geqslant2,\thinspace f\left(\ln\left(k\right)\right)\leqslant f\left(k\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-799d09980d5a25b823a488743a76e438_l3.png)
c’est-à-dire :
![Rendered by QuickLaTeX.com \[\forall k\geqslant2,\thinspace\frac{\ln\left(k\right)}{1+\ln\left(k\right)}\leqslant\frac{k}{1+k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f1863e751ef0186e20de73a7e85d1ad8_l3.png)
Il reste à multiplier membre à membre ces inégalités (entre réels positifs) pour
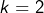
à

:
![Rendered by QuickLaTeX.com \[\prod_{k=2}^{n}\frac{\ln\left(k\right)}{1+\ln\left(k\right)}\leqslant\prod_{k=2}^{n}\frac{k}{1+k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-536c961c65b77265f98a92fbc22510ae_l3.png)
et à observer que ce dernier produit se télescope. Au final, pour tout entier

:
![Rendered by QuickLaTeX.com \[0\leqslant\prod_{k=2}^{n}\frac{\ln\left(k\right)}{1+\ln\left(k\right)}\leqslant\frac{2}{1+n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e8358255aa7e3f2509b6a31f2716ca3c_l3.png)
Il en résulte que :
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow\infty}\prod_{k=2}^{n}\frac{\ln\left(k\right)}{1+\ln\left(k\right)}=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0b2babdca73b1a45bdc0bf7da7063131_l3.png)
Le résultat établi dans cet exercice constitue une célèbre condition suffisante de convergence pour une série numérique, connue sous le nom de règle d’Abel.
Rappelons les notations. Etant donnée une suite 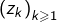 de nombres complexes, on pose :
de nombres complexes, on pose :
![Rendered by QuickLaTeX.com \[ S_{0}=0\qquad\text{et}\qquad\forall n\geqslant1,\thinspace S_{n}=\sum_{k=1}^{n}z_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d43bf2bd130b45268aae7b173980028b_l3.png)
On observe que, pour tout 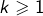 :
:
![Rendered by QuickLaTeX.com \[z_{k}=S_{k}-S_{k-1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2d1b6ec69c80a71996d008efa047e0bc_l3.png)
Par conséquent, pour tout
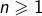
:
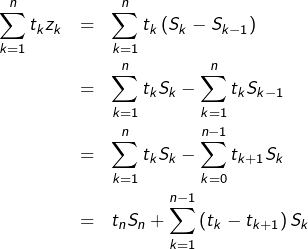
Noter que le terme 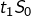 n’a pas été oublié dans cette dernière étape : il est nul.
n’a pas été oublié dans cette dernière étape : il est nul.
L’égalité :
![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=1}^{n}t_{k}z_{k}=t_{n}S_{n}+\sum_{k=1}^{n-1}\left(t_{k}-t_{k+1}\right)S_{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-585a12464177ab4740cbfbfc2473ac61_l3.png)
constitue ce qu’on appelle la
transformation d’Abel.
Remarque
Il s’agit, en quelque sorte, dune formule d’intégration par parties discrète.
Supposons la suite 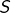 bornée et soit
bornée et soit 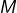 un majorant de celle-ci :
un majorant de celle-ci :
![Rendered by QuickLaTeX.com \[\forall k\geqslant1,\thinspace\left|S_{k}\right|\leqslant M\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1c5ca36cafd98a7a872537f6772de145_l3.png)
La série de terme général
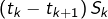
est absolument convergente (
donc convergente) car, d’une part, pour tout
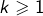
:
![Rendered by QuickLaTeX.com \[\left|\left(t_{k}-t_{k+1}\right)S_{k}\right|\leqslant M\left(t_{k}-t_{k+1}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-71e9c851c1286bd5e2bab70481259f85_l3.png)
et d’autre part, la série
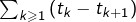
converge (et admet pour somme
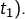
Il en résulte que la série de terme général 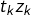 converge et admet pour somme :
converge et admet pour somme :
![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=1}^{\infty}t_{k}z_{k}=\sum_{k=1}^{\infty}\left(t_{k}-t_{k+1}\right)S_{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a4a648a68bac5568d6847e7047671e4c_l3.png)
On démontré la :
Règle d’Abel
Si 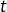 est une suite réelle décroissante de limite nulle et si
est une suite réelle décroissante de limite nulle et si 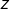 est une suite complexe dont la suite des sommes partielles est bornée, alors la série :
est une suite complexe dont la suite des sommes partielles est bornée, alors la série :
![Rendered by QuickLaTeX.com \[\sum_{k\geqslant1}t_kz_k\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-14f02a68b31251deac400ecf9c752009_l3.png)
est convergente.
Posons, pour tout 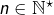 :
:
![Rendered by QuickLaTeX.com \[G_{n}=\sum_{k=1}^{n}e^{ik\theta}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-995b4077143f59f4cb3aeec40ec01772_l3.png)
Il s’agit d’une somme géométrique de raison
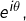
car
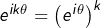
pour tout entier
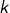
d’après la formule de Moivre. Comme par hypothèse

alors
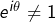
et donc :
![Rendered by QuickLaTeX.com \[G_{n}=\frac{e^{i\theta}\left(1-e^{in\theta}\right)}{1-e^{i\theta}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3e48bab4c1456afb6be1e860b2eb1690_l3.png)
que l’on peut encore écrire :
![Rendered by QuickLaTeX.com \[G_{n}=\frac{e^{i\theta}\thinspace e^{in\theta/2}}{e^{i\theta/2}}\:\frac{e^{-in\theta/2}-e^{in\theta/2}}{e^{i\theta/2}-e^{-i\theta/2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-83f3c68da42cf2e4c509fa17746f5e45_l3.png)
c’est-à-dire, d’après la formule d’Euler pour le sinus :
![Rendered by QuickLaTeX.com \[G_{n}=e^{i\left(n+1\right)\theta/2}\:\frac{\sin\left(\frac{n\theta}{2}\right)}{\sin\left(\frac{\theta}{2}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-25e0bac63ed9a733cb4f6fe8f86bdb9b_l3.png)
En récupérant les parties imaginaires de chaque membre, on obtient :
(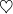 )
) ![Rendered by QuickLaTeX.com \[\boxed{B_{n}=\frac{\sin\left(\frac{n\theta}{2}\right)\thinspace\sin\left(\frac{\left(n+1\right)\theta}{2}\right)}{\sin\left(\frac{\theta}{2}\right)}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d65d2ff7633d03a1d07cfb3fda312523_l3.png)
Comme suggéré par l’énoncé, on peut aussi calculer directement :
![Rendered by QuickLaTeX.com \[\sin\left(\frac{\theta}{2}\right)B_{n}=\sum_{k=1}^{n}\sin\left(k\theta\right)\sin\left(\frac{\theta}{2}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-786466bcae3b9fb4e8d0bf1b535eb718_l3.png)
or, on peut linéariser chaque terme :
![Rendered by QuickLaTeX.com \[\sin\left(k\theta\right)\sin\left(\frac{\theta}{2}\right)=\frac{1}{2}\left[\cos\left(\left(k-\frac{1}{2}\right)\theta\right)-\cos\left(\left(k+\frac{1}{2}\right)\theta\right)\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-29743379f751b07e3de256fade12da89_l3.png)
ce qui donne une sommation télescopique :
![Rendered by QuickLaTeX.com \begin{eqnarray*} \sin\left(\frac{\theta}{2}\right)B_{n} & = & \frac{1}{2}\sum_{k=1}^{n}\left[\cos\left(\left(k-\frac{1}{2}\right)\theta\right)-\cos\left(\left(k+\frac{1}{2}\right)\theta\right)\right]\\ & = & \frac{1}{2}\left[\cos\left(\frac{\theta}{2}\right)-\cos\left(\left(n+\frac{1}{2}\right)\theta\right)\right]\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-4890181a55d227c71e00f9fd472356c8_l3.png)
et donc, vu que
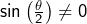
:
(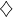 )
) ![Rendered by QuickLaTeX.com \[\boxed{B_{n}=\frac{\cos\left(\frac{\theta}{2}\right)-\cos\left(\left(n+\frac{1}{2}\right)\theta\right)}{2\sin\left(\frac{\theta}{2}\right)}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-81fd1ea6eb482e76a86724be1668bebf_l3.png)
En apparence, les résultats obtenus par les deux méthodes différent … mais en apparence seulement, car on sait bien que pour tout 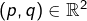 :
:
![Rendered by QuickLaTeX.com \[\cos\left(p\right)-\cos\left(q\right)=-2\sin\left(\frac{p+q}{2}\right)\sin\left(\frac{p-q}{2}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-29e65e80f556112ee7a6e602dcc47f18_l3.png)
Les formules  et
et  nous racontent donc la même histoire …
nous racontent donc la même histoire …
Considérons un ensemble  de cardinal
de cardinal 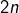 et deux parties
et deux parties 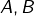 de
de 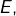 disjointes et de même cardinal
disjointes et de même cardinal 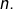
Se donner une partie de  de cardinal
de cardinal  revient à se donner, pour un certain
revient à se donner, pour un certain 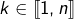 :
:
- une partie
 de
de 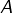 de cardinal
de cardinal 
- une partie
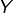 de
de 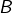 de cardinal
de cardinal 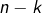
La partie  peut être choisie de
peut être choisie de 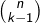 façons. Et pour chaque tel choix, la partie
façons. Et pour chaque tel choix, la partie 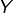 peut être choisie de
peut être choisie de 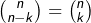 façons, ce qui donne un total de possibilités égal à :
façons, ce qui donne un total de possibilités égal à :
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n}\binom{n}{k-1}\binom{n}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-37bdc78cd25e263d3dd3e348514e007f_l3.png)
Bien entendu, le nombre parties de

de cardinal

est
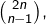
par définition !
Tout ceci prouve que :
![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=1}^{n}\binom{n}{k-1}\binom{n}{k}=\binom{2n}{n-1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-60dfcc2fa5f4625531e8da7c6aaa15a7_l3.png)
Posons :
![Rendered by QuickLaTeX.com \[\boxed{M\,\overline{M}=\left[x_{p,q}\right]_{1\leqslant p,q\leqslant n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d0ccbcd444a2a2cfbad516c666abe1cd_l3.png)
Vu que le conjugué d’un nombre complexe de module 1 coïncide avec son inverse :
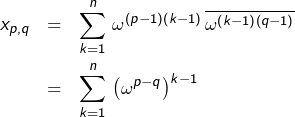
On reconnaît une somme géométrique de raison :
![Rendered by QuickLaTeX.com \[\omega^{p-q}=e^{2i\left(p-q\right)\pi/n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0ab9433276f96a2d7ae956fd9630c754_l3.png)
et l’on sait que, pour tout
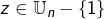
:
![Rendered by QuickLaTeX.com \[ \sum_{k=1}^{n}\,z^{k-1}=\frac{1-z^{n}}{1-z}=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cf3b3eacee02b8acc2a45b686af9924c_l3.png)
Or :
![Rendered by QuickLaTeX.com \[\omega^{p-q}=1\Leftrightarrow p-q\in n\mathbb{Z}\cap\llbracket-n+1,n-1\rrbracket =\left\{0\right\}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8258c32fb7aa2949ee75e49355e9452f_l3.png)
On voit ainsi que :
![Rendered by QuickLaTeX.com \[x_{p,q}=\left\{\begin{array}{ccc}n & \textrm{si} & p=q\\\\0 & \textrm{si} & p\neq q\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c09751c94a57fa0205e75d40dae52b47_l3.png)
Autrement dit :
![Rendered by QuickLaTeX.com \[\boxed{M\,\overline{M}=n\,I_{n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0b27d20188b242e45df57d6b3b0277c3_l3.png)
ce qui montre au passage que
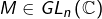
et que
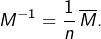
Posons :
![Rendered by QuickLaTeX.com \[\boxed{M^{2}=\left[y_{p,q}\right]_{1\leqslant p,q\leqslant n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2b20f3b0b87c8ecf2dbc5d8bd661f4af_l3.png)
Alors :
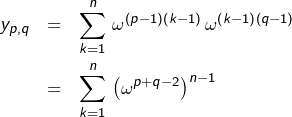
et donc :
![Rendered by QuickLaTeX.com \[y_{p,q}=\left\{ \begin{array}{ccc}n & \textrm{si} & p+q-2\not\equiv0\pmod{n}\\\\0 & \textrm{sinon}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6cc9331e32d928de8ac04e7e713517bc_l3.png)
Ainsi :
![Rendered by QuickLaTeX.com \[\boxed{M^{2}=n\,\left[\begin{array}{ccccc}1 & 0 & \cdots & \cdots & 0\\0 & 0 & \cdots & 0 & 1\\\vdots & \vdots & \iddots & \iddots & 0\\\vdots & 0 & \iddots & \iddots & \vdots\\0 & 1 & 0 & \cdots & 0\end{array}\right]}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e8b3eed94e47493ef211704b702bd964_l3.png)
On observe que :
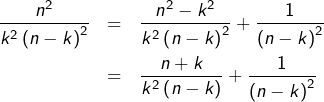
et donc, en remarquant que
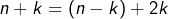
:
![Rendered by QuickLaTeX.com \[\frac{n^{2}}{k^{2}\left(n-k\right)^{2}}=\frac{1}{k^{2}}+\frac{1}{\left(n-k\right)^{2}}+\frac{2}{k\left(n-k\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-af3462aff441937e760305a89fdd60e7_l3.png)
Ainsi :
![Rendered by QuickLaTeX.com \[u_{n}=\frac{2}{n^{2}}\left[\sum_{k=1}^{n-1}\frac{1}{k^{2}}+\sum_{k=1}^{n-1}\frac{1}{k\left(n-k\right)}\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5563f6573c7f12fe4667a3e5c079303e_l3.png)
Or :
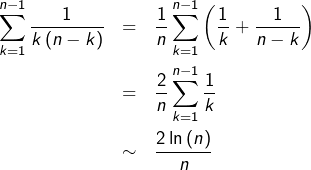
Cette dernière expression tend vers
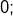
elle est donc négligeable devant
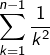
qui tend (résultat classique) vers
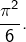
Par conséquent :
![Rendered by QuickLaTeX.com \[\boxed{u_{n}\sim\frac{\pi^{2}}{3n^{2}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9685ff924017698e8c7da365068b00c6_l3.png)
et la convergence de la série proposée en résulte.
Autre point de vue … Si vous savez ce qu’est le produit de Cauchy de deux séries numériques, vous constaterez que la série 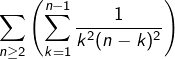 est le carré de Cauchy de la série
est le carré de Cauchy de la série 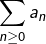 , avec :
, avec :
![Rendered by QuickLaTeX.com \[a_n=\left\{\begin{array}{ccc}{0 & \text{si }n=0\\ \frac{1}{n^2} & \text{sinon}}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b4e1e586125aebe7284ad4c1c6dffb42_l3.png)
Or, on sait (voir
cet article) que le produit de Cauchy de deux séries convergentes à termes positives (et, plus généralement, de deux séries absolument convergentes) converge et que sa somme est le produit des sommes. Ainsi, la série proposée converge et :
![Rendered by QuickLaTeX.com \[\sum_{n=2}^\infty\sum_{k=1}^{n-1}\frac{1}{k^2(n-k)^2}=\left(\sum_{n=1}^\infty\frac{1}{n^2}\right)^2=\frac{\pi^4}{36}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fda7c41c6ba1784f460506e1a0b4a687_l3.png)
La formule d’Euler pour le sinus donne, pour tout 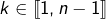 :
:
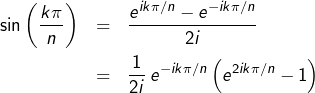
donc :
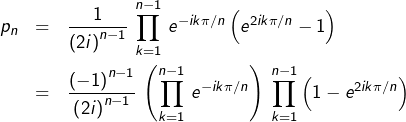
Or :
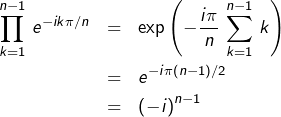
Ainsi :
![Rendered by QuickLaTeX.com \[\boxed{p_{n}=\frac{1}{2^{n-1}}\,\prod_{k=1}^{n-1}\,\left(1-e^{2ik\pi/n}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e3ece705591d1b1526afd32ae34e50d5_l3.png)
A présent, une bonne idée consiste à faire intervenir le polynôme :
![Rendered by QuickLaTeX.com \[Q_{n}=\prod_{k=1}^{n-1}\,\left(X-e^{2ik\pi/n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d5454df3b9b38dba65ac9ce5ee52c507_l3.png)
On sait d’une part que :
![Rendered by QuickLaTeX.com \[X^{n}-1=\prod_{k=0}^{n-1}\,\left(X-e^{2ik\pi/n}\right)=\left(X-1\right)\,Q_{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4796737013dd7bfb118c1c9de126f41d_l3.png)
et, d’autre part, que :
![Rendered by QuickLaTeX.com \[X^{n}-1=\left(X-1\right)\sum_{k=0}^{n-1}\,X^{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-13ba2ad1d924dd42e39dd95f49ed60f7_l3.png)
Il en résulte (par intégrité de l’anneau
![Rendered by QuickLaTeX.com \mathbb{C}\left[X\right])](https://math-os.com/wp-content/ql-cache/quicklatex.com-9adf7f7a91e95f769eb7e0c3d718eafd_l3.png)
que
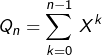
et donc que :
![Rendered by QuickLaTeX.com \[p_{n}=\frac{1}{2^{n-1}}\,Q_{n}\left(1\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9317ac5624e9fb8746c80f03e789d19b_l3.png)
d’où finalement :
![Rendered by QuickLaTeX.com \[\boxed{p_{n}=\frac{n}{2^{n-1}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c8d76341a890d79d39b5f76d13f6c889_l3.png)
Passons au calcul de l’intégrale impropre :
![Rendered by QuickLaTeX.com \[I=\int_{0}^{\pi/2}\ln\left(\sin\left(t\right)\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1b4c893baa44055315ff7a12234fdfb4_l3.png)
Nous allons
admettre et utiliser le résultat suivant :
Proposition
Si ![Rendered by QuickLaTeX.com f:\left]0,\pi\right[\rightarrow\mathbb{R}](https://math-os.com/wp-content/ql-cache/quicklatex.com-2af315ab0140e0780884a5caa44c1a07_l3.png) est continue et si l’intégrale impropre
est continue et si l’intégrale impropre 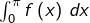 converge, alors :
converge, alors :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}\,\frac{\pi}{n}\sum_{k=1}^{n-1}\,f\left(\frac{k\pi}{n}\right)=\int_{0}^{\pi}f\left(x\right)\thinspace dx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1a260580ce2460014dfde4f11d63f107_l3.png)
L’application ![Rendered by QuickLaTeX.com f:\left]0,\pi\right[\rightarrow\mathbb{R},\thinspace t\mapsto\ln\left(\sin\left(t\right)\right)](https://math-os.com/wp-content/ql-cache/quicklatex.com-91e019322f85e244599853b7cf454359_l3.png) est continue. Au voisinage de 0 :
est continue. Au voisinage de 0 :
![Rendered by QuickLaTeX.com \[f\left(t\right)\underset{{\scriptstyle 0}}{\sim}\ln\left(t\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fb214c2697c7c39ac3024c564c8c229e_l3.png)
or on sait que
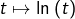
est intégrable et de signe fixe sur
![Rendered by QuickLaTeX.com \left]0,1\right].](https://math-os.com/wp-content/ql-cache/quicklatex.com-4f504d58286d960249cc931d4418fde3_l3.png)
Il s’ensuit que

est intégrable sur
![Rendered by QuickLaTeX.com \left]0,\frac{\pi}{2}\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7551e859aa107fd9f7a350e68560b624_l3.png)
et un argument de symétrie montre son intégrabilité sur
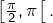
En outre, toujours en raison de la symétrie par rapport à
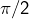
:
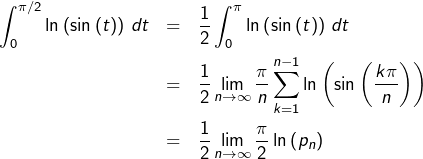
Soit finalement :
![Rendered by QuickLaTeX.com \[\boxed{\int_{0}^{\pi/2}\ln\left(\sin\left(t\right)\right)\thinspace dt=-\frac{\pi}{2}\ln\left(2\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8c74f3dd4daa9d8c353449a13b1cb309_l3.png)
Remarque
La résolution de cette question fait aussi l’objet d’une vidéo.
Procédons par récurrence. Pour 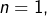 la formule est vraie.
la formule est vraie.
Supposons-la vraie au rang  pour un certain
pour un certain 
Dérivons, par rapport à 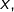 chaque membre de l’égalité à prouver.
chaque membre de l’égalité à prouver.
D’une part :
![Rendered by QuickLaTeX.com \[\frac{d}{dx}\left[\left(x+y\right)^{n}\right]=n\left(x+y\right)^{n-1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2cb586f560d9e21a1b679e26f9b71e9f_l3.png)
et d’autre part :
![Rendered by QuickLaTeX.com \begin{eqnarray*}& & \frac{d}{dx}\left[x^{n}+\sum_{k=1}^{n}\binom{n}{k}y\left(y-k\right)^{k-1}\left(x+k\right)^{n-k}\right]\\& = & nx^{n-1}+\sum_{k=1}^{n-1}\left(n-k\right)\binom{n}{k}y\left(y-k\right)^{k-1}\left(x+k\right)^{n-k-1}\\& \underset{\star}{=} & n\left(x^{n-1}+\sum_{k=1}^{n-1}\binom{n-1}{k}y\left(y-k\right)^{k-1}\left(x+k\right)^{\left(n-1\right)-k}\right)\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-22c241865c807df2a1b48f42724670fb_l3.png)
L’égalité  découle de la symétrie des coefficients binomiaux et de la formule du pion :
découle de la symétrie des coefficients binomiaux et de la formule du pion :
![Rendered by QuickLaTeX.com \[\left(n-k\right)\binom{n}{k}=\left(n-k\right)\binom{n}{n-k}=n\binom{n-1}{n-k-1}=n\binom{n-1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bdaa691571736a36cbd1c0f5530acc32_l3.png)
Bref, d’après l’hypothèse de récurrence, les dérivées sont égales.
Il suffit donc de prouver que les deux expressions qu’on a dérivées coïncident pour une certaine valeur de 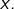 On prend
On prend 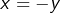 :
:
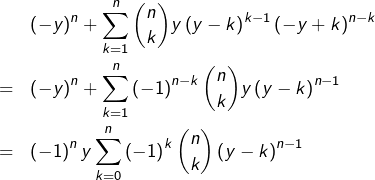
Or, en développant
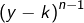
puis en intervertissant les sommes :
![Rendered by QuickLaTeX.com \begin{eqnarray*} & & \sum_{k=0}^{n}\left(-1\right)^{k}\binom{n}{k}\left(y-k\right)^{n-1}\\& = & \sum_{k=0}^{n}\left[\left(-1\right)^{k}\binom{n}{k}\sum_{j=0}^{n-1}\binom{n-1}{j}\left(-k\right)^{j}y^{n-1-j}\right]\\& = & \sum_{j=0}^{n-1}\left[\sum_{k=0}^{n}\left(-1\right)^{k}\binom{n}{k}k^{j}\right]\left(-1\right)^{j}\binom{n-1}{j}y^{n-1-j}\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-4f3cd72f0390f89d375c8f2082cc3aa4_l3.png)
Or, il se trouve que :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N}^{\star},\thinspace\forall j\in\left\llbracket 0,n-1\right\rrbracket ,\thinspace\sum_{k=0}^{n}\left(-1\right)^{k}\binom{n}{k}k^{j}=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3bf1df57616fdba6fdff0416fb54532c_l3.png)
ce qui permet de conclure.
![Rendered by QuickLaTeX.com \[ S_{p,q}=\sum_{k=p}^{q}u_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cd36fbccd6156d9ad8dcd47d7e6d7de1_l3.png)
![Rendered by QuickLaTeX.com \[2\thinspace S_{p,q}=\sum_{k=p}^{q}\left(u_{k}+u_{q+p-k}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5e86102a92306b1cd9b7289952831174_l3.png)
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\prod_{k=2}^{n}\frac{\ln\left(k\right)}{1+\ln\left(k\right)}\leqslant\prod_{k=2}^{n}\frac{k}{1+k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-536c961c65b77265f98a92fbc22510ae_l3.png)
![Rendered by QuickLaTeX.com \[0\leqslant\prod_{k=2}^{n}\frac{\ln\left(k\right)}{1+\ln\left(k\right)}\leqslant\frac{2}{1+n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e8358255aa7e3f2509b6a31f2716ca3c_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow\infty}\prod_{k=2}^{n}\frac{\ln\left(k\right)}{1+\ln\left(k\right)}=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0b2babdca73b1a45bdc0bf7da7063131_l3.png)
![]() de nombres complexes, on pose :
de nombres complexes, on pose : ![Rendered by QuickLaTeX.com \[ S_{0}=0\qquad\text{et}\qquad\forall n\geqslant1,\thinspace S_{n}=\sum_{k=1}^{n}z_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d43bf2bd130b45268aae7b173980028b_l3.png)
![]() :
:![]()
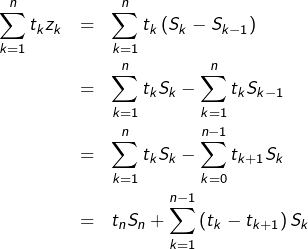
![]() n’a pas été oublié dans cette dernière étape : il est nul.
n’a pas été oublié dans cette dernière étape : il est nul.![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=1}^{n}t_{k}z_{k}=t_{n}S_{n}+\sum_{k=1}^{n-1}\left(t_{k}-t_{k+1}\right)S_{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-585a12464177ab4740cbfbfc2473ac61_l3.png)
![]() bornée et soit
bornée et soit ![]() un majorant de celle-ci :
un majorant de celle-ci :![]()
![]()
![]() converge et admet pour somme :
converge et admet pour somme :![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=1}^{\infty}t_{k}z_{k}=\sum_{k=1}^{\infty}\left(t_{k}-t_{k+1}\right)S_{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a4a648a68bac5568d6847e7047671e4c_l3.png)
![]() est une suite réelle décroissante de limite nulle et si
est une suite réelle décroissante de limite nulle et si ![]() est une suite complexe dont la suite des sommes partielles est bornée, alors la série :
est une suite complexe dont la suite des sommes partielles est bornée, alors la série :![]()
![Rendered by QuickLaTeX.com \[G_{n}=\sum_{k=1}^{n}e^{ik\theta}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-995b4077143f59f4cb3aeec40ec01772_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[G_{n}=e^{i\left(n+1\right)\theta/2}\:\frac{\sin\left(\frac{n\theta}{2}\right)}{\sin\left(\frac{\theta}{2}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-25e0bac63ed9a733cb4f6fe8f86bdb9b_l3.png)
![]() )
) ![Rendered by QuickLaTeX.com \[\boxed{B_{n}=\frac{\sin\left(\frac{n\theta}{2}\right)\thinspace\sin\left(\frac{\left(n+1\right)\theta}{2}\right)}{\sin\left(\frac{\theta}{2}\right)}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d65d2ff7633d03a1d07cfb3fda312523_l3.png)
![Rendered by QuickLaTeX.com \[\sin\left(\frac{\theta}{2}\right)B_{n}=\sum_{k=1}^{n}\sin\left(k\theta\right)\sin\left(\frac{\theta}{2}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-786466bcae3b9fb4e8d0bf1b535eb718_l3.png)
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*} \sin\left(\frac{\theta}{2}\right)B_{n} & = & \frac{1}{2}\sum_{k=1}^{n}\left[\cos\left(\left(k-\frac{1}{2}\right)\theta\right)-\cos\left(\left(k+\frac{1}{2}\right)\theta\right)\right]\\ & = & \frac{1}{2}\left[\cos\left(\frac{\theta}{2}\right)-\cos\left(\left(n+\frac{1}{2}\right)\theta\right)\right]\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-4890181a55d227c71e00f9fd472356c8_l3.png)
![]() )
) ![Rendered by QuickLaTeX.com \[\boxed{B_{n}=\frac{\cos\left(\frac{\theta}{2}\right)-\cos\left(\left(n+\frac{1}{2}\right)\theta\right)}{2\sin\left(\frac{\theta}{2}\right)}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-81fd1ea6eb482e76a86724be1668bebf_l3.png)
![]()
 de
de  de cardinal
de cardinal 
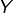 de
de 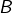 de cardinal
de cardinal 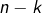
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n}\binom{n}{k-1}\binom{n}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-37bdc78cd25e263d3dd3e348514e007f_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=1}^{n}\binom{n}{k-1}\binom{n}{k}=\binom{2n}{n-1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-60dfcc2fa5f4625531e8da7c6aaa15a7_l3.png)
![]()
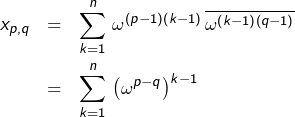
![]()
![Rendered by QuickLaTeX.com \[ \sum_{k=1}^{n}\,z^{k-1}=\frac{1-z^{n}}{1-z}=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cf3b3eacee02b8acc2a45b686af9924c_l3.png)
![]()
![Rendered by QuickLaTeX.com \[x_{p,q}=\left\{\begin{array}{ccc}n & \textrm{si} & p=q\\\\0 & \textrm{si} & p\neq q\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c09751c94a57fa0205e75d40dae52b47_l3.png)
![]()
![]()
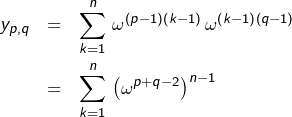
![Rendered by QuickLaTeX.com \[y_{p,q}=\left\{ \begin{array}{ccc}n & \textrm{si} & p+q-2\not\equiv0\pmod{n}\\\\0 & \textrm{sinon}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6cc9331e32d928de8ac04e7e713517bc_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{M^{2}=n\,\left[\begin{array}{ccccc}1 & 0 & \cdots & \cdots & 0\\0 & 0 & \cdots & 0 & 1\\\vdots & \vdots & \iddots & \iddots & 0\\\vdots & 0 & \iddots & \iddots & \vdots\\0 & 1 & 0 & \cdots & 0\end{array}\right]}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e8b3eed94e47493ef211704b702bd964_l3.png)
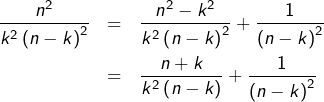
![]()
![Rendered by QuickLaTeX.com \[u_{n}=\frac{2}{n^{2}}\left[\sum_{k=1}^{n-1}\frac{1}{k^{2}}+\sum_{k=1}^{n-1}\frac{1}{k\left(n-k\right)}\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5563f6573c7f12fe4667a3e5c079303e_l3.png)
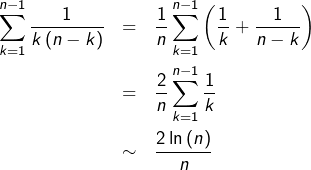
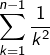 qui tend (résultat classique) vers
qui tend (résultat classique) vers ![Rendered by QuickLaTeX.com \[\boxed{u_{n}\sim\frac{\pi^{2}}{3n^{2}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9685ff924017698e8c7da365068b00c6_l3.png)
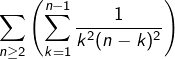 est le carré de Cauchy de la série
est le carré de Cauchy de la série ![]() , avec :
, avec :![]()
![Rendered by QuickLaTeX.com \[\sum_{n=2}^\infty\sum_{k=1}^{n-1}\frac{1}{k^2(n-k)^2}=\left(\sum_{n=1}^\infty\frac{1}{n^2}\right)^2=\frac{\pi^4}{36}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fda7c41c6ba1784f460506e1a0b4a687_l3.png)

![]() :
: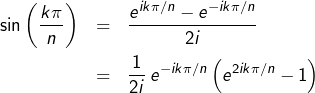
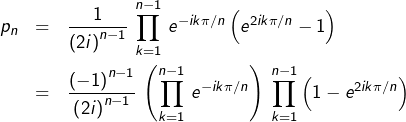
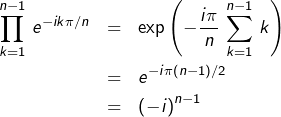
![Rendered by QuickLaTeX.com \[\boxed{p_{n}=\frac{1}{2^{n-1}}\,\prod_{k=1}^{n-1}\,\left(1-e^{2ik\pi/n}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e3ece705591d1b1526afd32ae34e50d5_l3.png)
![Rendered by QuickLaTeX.com \[Q_{n}=\prod_{k=1}^{n-1}\,\left(X-e^{2ik\pi/n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d5454df3b9b38dba65ac9ce5ee52c507_l3.png)
![Rendered by QuickLaTeX.com \[X^{n}-1=\prod_{k=0}^{n-1}\,\left(X-e^{2ik\pi/n}\right)=\left(X-1\right)\,Q_{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4796737013dd7bfb118c1c9de126f41d_l3.png)
![Rendered by QuickLaTeX.com \[X^{n}-1=\left(X-1\right)\sum_{k=0}^{n-1}\,X^{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-13ba2ad1d924dd42e39dd95f49ed60f7_l3.png)
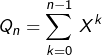 et donc que :
et donc que :![]()
![]()
![]()
![]() est continue et si l’intégrale impropre
est continue et si l’intégrale impropre ![]() converge, alors :
converge, alors :![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}\,\frac{\pi}{n}\sum_{k=1}^{n-1}\,f\left(\frac{k\pi}{n}\right)=\int_{0}^{\pi}f\left(x\right)\thinspace dx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1a260580ce2460014dfde4f11d63f107_l3.png)
![]() est continue. Au voisinage de 0 :
est continue. Au voisinage de 0 :![]()
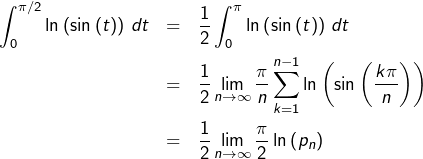
![Rendered by QuickLaTeX.com \[\boxed{\int_{0}^{\pi/2}\ln\left(\sin\left(t\right)\right)\thinspace dt=-\frac{\pi}{2}\ln\left(2\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8c74f3dd4daa9d8c353449a13b1cb309_l3.png)

![]() la formule est vraie.
la formule est vraie.![]() pour un certain
pour un certain ![]()
![]() chaque membre de l’égalité à prouver.
chaque membre de l’égalité à prouver.![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}& & \frac{d}{dx}\left[x^{n}+\sum_{k=1}^{n}\binom{n}{k}y\left(y-k\right)^{k-1}\left(x+k\right)^{n-k}\right]\\& = & nx^{n-1}+\sum_{k=1}^{n-1}\left(n-k\right)\binom{n}{k}y\left(y-k\right)^{k-1}\left(x+k\right)^{n-k-1}\\& \underset{\star}{=} & n\left(x^{n-1}+\sum_{k=1}^{n-1}\binom{n-1}{k}y\left(y-k\right)^{k-1}\left(x+k\right)^{\left(n-1\right)-k}\right)\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-22c241865c807df2a1b48f42724670fb_l3.png)
![]() découle de la symétrie des coefficients binomiaux et de la formule du pion :
découle de la symétrie des coefficients binomiaux et de la formule du pion :![]()
![]() On prend
On prend ![]() :
: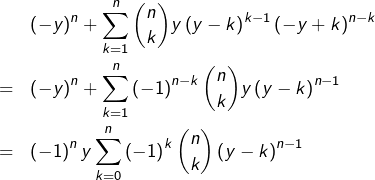
![Rendered by QuickLaTeX.com \begin{eqnarray*} & & \sum_{k=0}^{n}\left(-1\right)^{k}\binom{n}{k}\left(y-k\right)^{n-1}\\& = & \sum_{k=0}^{n}\left[\left(-1\right)^{k}\binom{n}{k}\sum_{j=0}^{n-1}\binom{n-1}{j}\left(-k\right)^{j}y^{n-1-j}\right]\\& = & \sum_{j=0}^{n-1}\left[\sum_{k=0}^{n}\left(-1\right)^{k}\binom{n}{k}k^{j}\right]\left(-1\right)^{j}\binom{n-1}{j}y^{n-1-j}\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-4f3cd72f0390f89d375c8f2082cc3aa4_l3.png)
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N}^{\star},\thinspace\forall j\in\left\llbracket 0,n-1\right\rrbracket ,\thinspace\sum_{k=0}^{n}\left(-1\right)^{k}\binom{n}{k}k^{j}=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3bf1df57616fdba6fdff0416fb54532c_l3.png)