Montrer que, pour tout entier ![]() le coefficient binomial central
le coefficient binomial central ![]() est pair.
est pair.

Soient ![]() deux entiers tels que
deux entiers tels que ![]() Prouver que :
Prouver que :
![]()

Etant donnés des entiers ![]() et
et ![]() tels que
tels que ![]() et
et ![]() calculer plus simplement :
calculer plus simplement :
![Rendered by QuickLaTeX.com \[\sum_{i=0}^{k}\left(-1\right)^{i}\binom{n}{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ecbc4bd7e9d58461cf696e4e2452f93c_l3.png)

Soit ![]() Calculer plus simplement la somme :
Calculer plus simplement la somme :
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{p}\left(-1\right)^{k}\left[\binom{2p}{k}-\binom{2p}{k-1}\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9bc6a83337296efa940df6f402ea360f_l3.png)

Trouver un équivalent, lorsque ![]() du
du ![]() ème coefficient binomial central
ème coefficient binomial central ![]()

Soient ![]() des entiers tels que
des entiers tels que ![]() Montrer que :
Montrer que :
![]()
Quelle formule présente dans cet article ce résultat généralise-t-il ?

Pour tout entier ![]() on pose :
on pose :
![]()
![]()

![]()
![]()
- Combien existe-t-il de chaînes ? Combien d’entre-elles comportent une partie
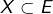 donnée ?
donnée ? - Montrer qu’il existe une antichaîne de cardinal
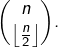
- Soit
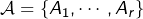 une antichaîne. Pour tout
une antichaîne. Pour tout 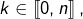 on note
on note 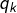 le nombre d’éléments de
le nombre d’éléments de 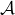 qui sont de cardinal
qui sont de cardinal 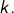
- Montrer que
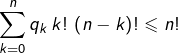
- Conclure.
- Montrer que


