Solutions détaillées de neuf exercices sur les coefficients binomiaux (fiche 02)
Cliquer ici pour accéder aux énoncés

Dans l’expression développée de ![]() les termes en
les termes en ![]() s’obtiennent en sélectionnant
s’obtiennent en sélectionnant ![]() dans 4 parenthèses, ce qui peut se faire de
dans 4 parenthèses, ce qui peut se faire de ![]() façons et, pour chaque tel choix, en sélectionnant
façons et, pour chaque tel choix, en sélectionnant ![]() dans 3 parenthèses parmi les 5 restantes, ce qui peut se faire de
dans 3 parenthèses parmi les 5 restantes, ce qui peut se faire de ![]() façons (il reste ensuite 2 parenthèses où l’on doit fatalement sélectionner
façons (il reste ensuite 2 parenthèses où l’on doit fatalement sélectionner ![]()
Le coefficient de ![]() dans le développement de
dans le développement de ![]() est donc :
est donc :
![]()
Pour tout entier ![]() on a d’après la formule de Pascal :
on a d’après la formule de Pascal :
![]()
![]()
![]()
Remarque
Plus précisément : l’exposant de ![]() dans la décomposition en facteurs premiers de
dans la décomposition en facteurs premiers de ![]() est égal au nombre de 1 dans l’écriture binaire de
est égal au nombre de 1 dans l’écriture binaire de ![]() Cet entier étant non nul puisque
Cet entier étant non nul puisque ![]() on retrouve ainsi la parité de
on retrouve ainsi la parité de ![]() Pour une preuve de ce résultat, voir cet article.
Pour une preuve de ce résultat, voir cet article.
On sait que :
![Rendered by QuickLaTeX.com \[\binom{n}{k}=\frac{n\left(n-1\right)\cdots\left(n-k+1\right)}{k!}=\prod_{j=0}^{k-1}\frac{n-j}{k-j}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7a92a5b79776b98cca7cc401fddb0ea0_l3.png)
(![]() )
) ![]()
![Rendered by QuickLaTeX.com \[\boxed{\binom{n}{k}\geqslant\left(\frac{n}{k}\right)^{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ac6c291b5cecdb4e0e2b9e80f066d770_l3.png)
![]()

Soient ![]() des entiers tels que
des entiers tels que ![]() D’après la formule de Pascal :
D’après la formule de Pascal :
![Rendered by QuickLaTeX.com \begin{eqnarray*}\sum_{i=0}^{k}\left(-1\right)^{i}\binom{n}{i} & = & 1+\sum_{i=1}^{k}\left(-1\right)^{i}\left[\binom{n-1}{i}+\binom{n-1}{i-1}\right]\\& = & 1+\sum_{i=1}^{k}\left[\left(-1\right)^{i}\binom{n-1}{i}-\left(-1\right)^{i}\binom{n-1}{i-1}\right]\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-5f7e4182a498d051b226dadee74727d8_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=0}^{k}\left(-1\right)^{i}\binom{n}{i}=\left(-1\right)^{k}\binom{n-1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9c4871dfa610f721d8724d5cfc0e0e54_l3.png)
Remarque
Pour ![]() on trouve
on trouve 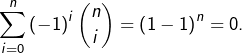 La formule obtenue pour
La formule obtenue pour ![]() s’applique donc aussi lorsque
s’applique donc aussi lorsque ![]()

Notons ![]() cette somme. On peut la séparer en deux :
cette somme. On peut la séparer en deux :
![Rendered by QuickLaTeX.com \[S_{p}=\sum_{k=1}^{p}\left(-1\right)^{k}\binom{2p}{k}+\sum_{k=1}^{p}\left(-1\right)^{k-1}\binom{2p}{k-1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b8b7e996a0b5c17e5af8af3ae27d648f_l3.png)
![Rendered by QuickLaTeX.com \[S_{p}=\sum_{k=1}^{p}\left(-1\right)^{k}\binom{2p}{k}+\sum_{j=p+1}^{2p}\left(-1\right)^{2p-j}\binom{2p}{2p-j}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f352ad279ce84cb559d39d30ef57cbca_l3.png)
![Rendered by QuickLaTeX.com \[S_{p}=\sum_{k=1}^{2p}\left(-1\right)^{k}\binom{2p}{k}=-1+\left(1-1\right)^{2p}=-1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-113ee995601c6986c0c98b4f83c68e97_l3.png)
Remarque
On peut aussi exploiter le résultat de l’exercice précédent :
![Rendered by QuickLaTeX.com \begin{eqnarray*}S_{p} & = & \sum_{k=1}^{p}\left(-1\right)^{k}\left[\binom{2p}{k}-\binom{2p}{k-1}\right]\\& = & \sum_{k=1}^{p}\left(-1\right)^{k}\binom{2p}{k}+\sum_{k=0}^{p-1}\left(-1\right)^{k}\binom{2p}{k}\\& = & -1+\sum_{k=0}^{p}\left(-1\right)^{k}\binom{2p}{k}+\sum_{k=0}^{p-1}\left(-1\right)^{k}\binom{2p}{k}\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-c3d97c48e8eeba6c319691a9a2af419e_l3.png)

Si l’on connaît la formule de Stirling :
![]()
![Rendered by QuickLaTeX.com \[\binom{2n}{n}=\frac{\left(2n\right)!}{\left(n!\right)^{2}}\sim\frac{\left(\frac{2n}{e}\right)^{2n}\sqrt{4\pi n}}{\left(\left(\frac{n}{e}\right)^{n}\sqrt{2\pi n}\right)^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-41bb2b9701d6796aae2b75300a15e716_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\binom{2n}{n}\sim\frac{4^{n}}{\sqrt{\pi n}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4dfecdc81992e0281d84fd5b83a78abf_l3.png)

Commençons par une preuve algébrique (calculatoire … donc pas passionnante). D’une part :
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{\binom{r}{q}\binom{q}{p}=\binom{r}{p}\binom{r-p}{q-p}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-de82362c3bb392d99e0c0a85911f8210_l3.png)
![]()
![]()
![]()
Remarque
Pour ![]() et toujours
et toujours ![]() , cette formule devient :
, cette formule devient :
![]()

Calculons, pour tout entier ![]() :
:
![]()
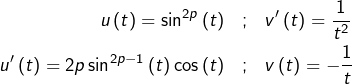
![]()
![Rendered by QuickLaTeX.com \[\sin^{2p-1}\left(x\right)=\frac{1}{4^{p-1}}\sum_{k=0}^{p-1}\left(-1\right)^{k}\binom{2p-1}{p-1-k}\sin\left(\left(2k+1\right)x\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d1d5b311f6d5442ebd81129beda4862d_l3.png)
![Rendered by QuickLaTeX.com \[J_{p}=\dfrac{2p}{4^{p-1}}\sum_{k=0}^{p-1}\left(-1\right)^{k}\binom{2p-1}{p-1-k}\int_{0}^{+\infty}\dfrac{\sin\left(\left(2k+1\right)t\right)\cos\left(t\right)}{t}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b062ca0a969baaace35d3a7b1a4c7581_l3.png)
![Rendered by QuickLaTeX.com \[J_{p}=\dfrac{p}{4^{p-1}}\sum_{k=0}^{p-1}\left(-1\right)^{k}\binom{2p-1}{p-1-k}\int_{0}^{+\infty}\dfrac{\sin\left(\left(2k+2\right)t\right)+\sin\left(2kt\right)}{t}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2aa12621cbb5b03683282eb84f874135_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\int_{0}^{+\infty}\dfrac{\sin\left(\left(2k+2\right)t\right)+\sin\left(2kt\right)}{t}\thinspace dt=\left\{ \begin{array}{cc}\pi & \text{si }k\geqslant1\\\\\dfrac{\pi}{2} & \text{si }k=0\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a54857a639c8484a3f8adfec6dc30c44_l3.png)
![Rendered by QuickLaTeX.com \[J_{p}=\dfrac{p\pi}{2^{2p-1}}\left[\binom{2p-1}{p-1}+2\sum_{k=1}^{p-1}\left(-1\right)^{k}\binom{2p-1}{p-1-k}\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6435cf83df1bfa4e8ad6e5e2090e24b0_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*}J_{p} & = & \dfrac{p\pi}{2^{2p-1}}\left[\binom{2p-1}{p-1}+2\left(-1\right)^{p-1}\sum_{j=0}^{p-2}\left(-1\right)^{j}\binom{2p-1}{j}\right]\\& = & \dfrac{p\pi}{2^{2p-1}}\left[\binom{2p-1}{p-1}-2\binom{2p-2}{p-2}\right]\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-8af88aff72de817b0c4e4a88e9dfc0c5_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{J_{p}=\dfrac{\pi}{2^{2p-1}}\binom{2p-2}{p-1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-898d88aa005ac29157850616e39dfc20_l3.png)

- L’application qui, à une chaine
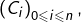 associe la permutation
associe la permutation  définie par
définie par
est une bijection. Il existe donc![Rendered by QuickLaTeX.com \[\forall i\in\left\llbracket 1,n\right\rrbracket ,\thinspace\left\{ \sigma\left(i\right)\right\} =C_{i}-C_{i-1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-61439e3cbb16bcb344f1ba1da2259123_l3.png)
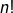 chaînes. Soit maintenant
chaînes. Soit maintenant  une partie de
une partie de 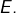 Notons
Notons 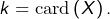 Dire que
Dire que  fait partie d’une chaîne
fait partie d’une chaîne 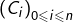 signifie que
signifie que 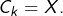 Il existe
Il existe 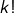 façons de contruire la sous-chaîne
façons de contruire la sous-chaîne 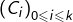 puis, pour chaque tel choix,
puis, pour chaque tel choix, 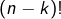 façons de prolonger celle-ci en une chaîne. Au total, le nombre de chaînes « passant par
façons de prolonger celle-ci en une chaîne. Au total, le nombre de chaînes « passant par  » est
» est 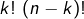
- Pour tout
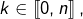 l’ensemble des parties de
l’ensemble des parties de 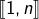 qui sont de cardinal
qui sont de cardinal 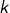 est une antichaîne, de cardinal
est une antichaîne, de cardinal 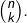 En particulier pour
En particulier pour 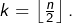
- Une majoration :
- Pour tout
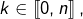 notons
notons 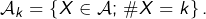 Par définition :
Par définition : 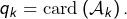 Comme
Comme 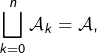 on voit en passant aux cardinaux que :
on voit en passant aux cardinaux que :
Pour chaque![Rendered by QuickLaTeX.com \[{\displaystyle \sum_{k=0}^{n}q_{k}}=r\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-56fcf77a20ccb3def346b270077fdb49_l3.png)
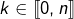 et pour chaque élément
et pour chaque élément 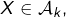 on considère les
on considère les 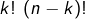 chaînes qui passent par
chaînes qui passent par 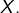 Ceci représente un total de
Ceci représente un total de 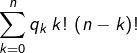 chaînes, car une même chaîne ne peut pas passer par deux éléments distincts de
chaînes, car une même chaîne ne peut pas passer par deux éléments distincts de 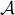 (sans quoi il existerait une relation d’inclusion entre ces deux éléments de
(sans quoi il existerait une relation d’inclusion entre ces deux éléments de 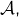 ce qui est absurde). Ce total étant majoré par le nombre chaînes, il vient :
ce qui est absurde). Ce total étant majoré par le nombre chaînes, il vient :![Rendered by QuickLaTeX.com \[\sum_{k=0}^{n}q_{k}\thinspace k!\thinspace\left(n-k\right)!\leqslant n!\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-39e5a0ee4ae8bd34082c4c24db8a217b_l3.png)
- L’inégalité précédente peut s’écrire :
Or, on sait que :![Rendered by QuickLaTeX.com \[\sum_{k=0}^{n}\frac{q_{k}}{\binom{n}{k}}\leqslant1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4953a1f645e9c49eb1e884b163e2bb2a_l3.png)
Il s’ensuit que :![Rendered by QuickLaTeX.com \[\forall k\in\left\llbracket 0,n\right\rrbracket ,\thinspace\binom{n}{k}\leqslant\binom{n}{\left\lfloor \frac{n}{2}\right\rfloor }\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e4611ed39ae8e90c2d8933c3ca628d61_l3.png)
c’est-à-dire (cf. 3°-A) :![Rendered by QuickLaTeX.com \[\sum_{k=0}^{n}q_{k}\leqslant\binom{n}{\left\lfloor \frac{n}{2}\right\rfloor }\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2a9435892a79bdf8e22054a7df7e16ee_l3.png)
Compte tenu du 2°, on conclut que le cardinal maximal d’une antichaîne est![Rendered by QuickLaTeX.com \[r\leqslant\binom{n}{\left\lfloor \frac{n}{2}\right\rfloor }\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-63e723f2631b0709e1403c97bd01e488_l3.png)
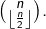
- Pour tout
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.

