Neuf énoncés d’exercices sur la notion d’application (fiche 01).

Chacun des dessins ci-dessous représente une correspondance. Expliquer, dans chaque cas, s’il s’agit d’une application et – le cas échéant – d’une injection, d’une surjection, voire d’une bijection :
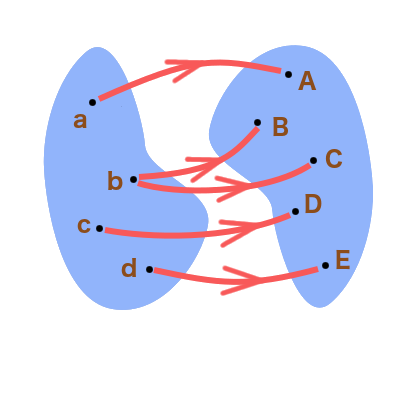
u 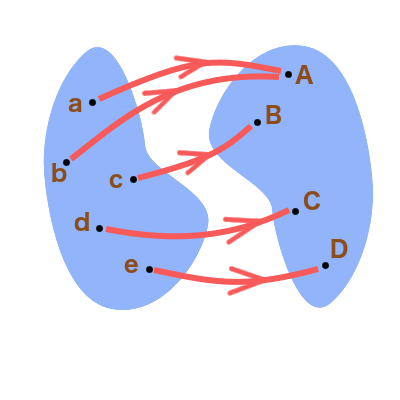
v 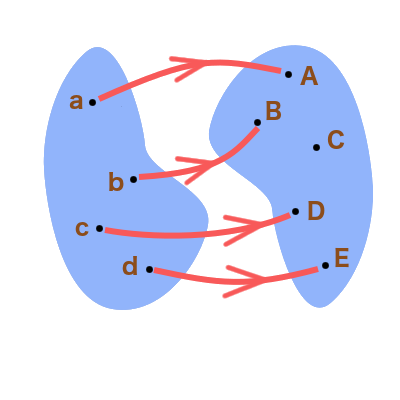
w 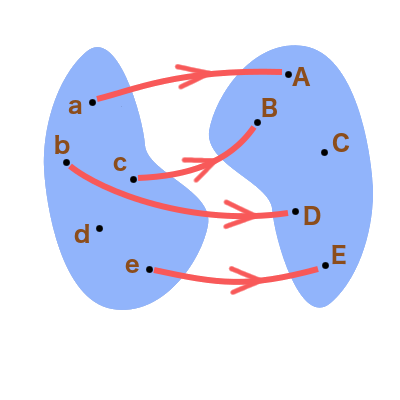
f 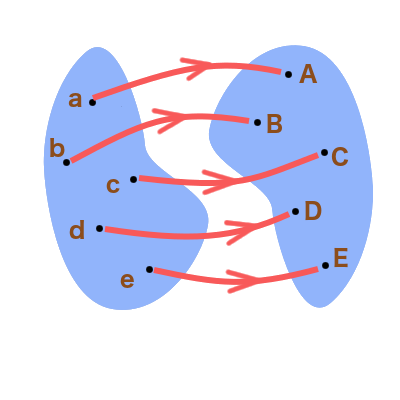
g 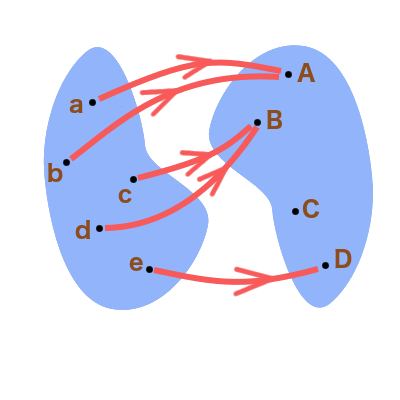
h

Préciser, pour chaque application, si elle est injective (ou non), surjective (ou non) :
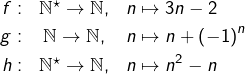
Comparer avec l’exercice suivant.

Pour chacune des applications suivantes, préciser s’il s’agit d’une injection (ou non), d’une surjection (ou non) :
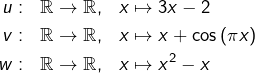
Comparer avec l’exercice précédent.

Montrer que l’application
![]()
En déduire que l’application
![]()

Proposer un exemple d’application de ![]() dans
dans ![]() qui soit injective et non surjective. Proposer aussi un exemple d’application de
qui soit injective et non surjective. Proposer aussi un exemple d’application de ![]() dans
dans ![]() qui soit surjective et non injective.
qui soit surjective et non injective.

Donner un exemple d’application périodique et surjective de ![]() dans
dans ![]()

Trouver deux applications ![]() injectives telles que
injectives telles que ![]()
Une application injective ![]() est nécessairement strictement monotone : Vrai ou Faux ?
est nécessairement strictement monotone : Vrai ou Faux ?

Soit ![]() un ensemble non vide et soit
un ensemble non vide et soit ![]() une application.
une application.
Pour tout ![]() on note
on note ![]() la
la ![]() ème itérée de
ème itérée de ![]()
On rappelle la…
Définition
![]()
Montrer que si
![]()
alors
Cliquer ici pour accéder aux indications
Cliquer ici pour accéder aux solutions

