Un espace préhilbertien réel (EPHR) ![]() est un
est un ![]() espace vectoriel qu’on a muni d’un produit scalaire. Si cette notion n’est pas claire, on pourra se reporter à cet article, dont la première section contient les rappels nécessaires.
espace vectoriel qu’on a muni d’un produit scalaire. Si cette notion n’est pas claire, on pourra se reporter à cet article, dont la première section contient les rappels nécessaires.
Le produit scalaire de deux vecteurs ![]() sera noté
sera noté ![]()
Si ![]() est en outre de dimension finie, on parle plutôt d’espace vectoriel euclidien (EVE).
est en outre de dimension finie, on parle plutôt d’espace vectoriel euclidien (EVE).
Dans un EVE de dimension n, une base ![]() est dite orthonormale (BON en abrégé) si elle est formée de vecteurs unitaires (càd : de norme 1) et deux à deux orthogonaux. Il revient au même de dire qu’il s’agit d’une famille orthonormale et génératrice de
est dite orthonormale (BON en abrégé) si elle est formée de vecteurs unitaires (càd : de norme 1) et deux à deux orthogonaux. Il revient au même de dire qu’il s’agit d’une famille orthonormale et génératrice de ![]() puisque « orthonormale » implique « libre ».
puisque « orthonormale » implique « libre ».
Proposition
Si ![]() est une BON de l’EVE
est une BON de l’EVE ![]() alors :
alors :
(A) ![Rendered by QuickLaTeX.com \[\forall x\in E,\thinspace x=\sum_{i=1}^{n}\left(x\mid e_{i}\right)e_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e04b65f2b60dad70748dff8cd440a86d_l3.png)
En effet, on peut décomposer tout vecteur ![]() dans la base
dans la base ![]() sous la forme :
sous la forme :
![Rendered by QuickLaTeX.com \[x=\sum_{k=1}^{n}x_{k}e_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c49a165485e71cafc46a9b99200b8145_l3.png)
![Rendered by QuickLaTeX.com \[\left(x\mid e_{i}\right)=\sum_{k=1}^{n}x_{k}\left(e_{k}\mid e_{i}\right)=\sum_{k=1}^{n}x_{k}\delta_{k,i}=x_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e946b48ac8d1d8c3e6be8ccbefc840c2_l3.png)
Corollaire
Si ![]() est une BON de l’EVE
est une BON de l’EVE ![]() alors :
alors :
(B) ![Rendered by QuickLaTeX.com \[\forall x\in E,\thinspace\left\Vert x\right\Vert ^{2}=\sum_{i=1}^{n}\left(x\mid e_{i}\right)^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7664d1c92c5724489e9bfe8f191a3fed_l3.png)
En partant de l’assertion (A) et en effectuant le produit scalaire de chaque membre par ![]() on obtient directement (B). On peut aussi utiliser la formule de Pythagore (le carré de la norme d’une somme de vecteurs deux à deux orthogonaux est égale à la somme des carrés des normes de ces vecteurs); pour tout
on obtient directement (B). On peut aussi utiliser la formule de Pythagore (le carré de la norme d’une somme de vecteurs deux à deux orthogonaux est égale à la somme des carrés des normes de ces vecteurs); pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\left\Vert x\right\Vert ^{2}=\left\Vert \sum_{i=1}^{n}\left(x\mid e_{i}\right)e_{i}\right\Vert ^{2}=\sum_{i=1}^{n}\left(x\mid e_{i}\right)^{2}\left\Vert e_{i}\right\Vert ^{2}=\sum_{i=1}^{n}\left(x\mid e_{i}\right)^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-83cd7c260a018c12e4cefc8415791c36_l3.png)
A présent, étant donné un EPHR ![]() et une famille
et une famille ![]() de vecteurs de
de vecteurs de ![]() on va s’interroger sur les réciproques de la proposition et de son corollaire :
on va s’interroger sur les réciproques de la proposition et de son corollaire :
- Les assertions (A) ou (B) suffisent-elles pour entraîner que
 est une BON de
est une BON de  ?
? - Et si tel n’est pas le cas, que peut-on supposer de plus pour atteindre cette conclusion ?
1 – Réciproque de (A)
Proposition
Soit ![]() un EVE de dimension
un EVE de dimension ![]() et soit
et soit ![]() une famille de vecteurs de
une famille de vecteurs de ![]() vérifiant :
vérifiant :
![Rendered by QuickLaTeX.com \[\forall x\in E,\,x=\sum_{i=1}^{n}\,\left(x\mid e_{i}\right)e_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cb1913321653f2426a8421b3bf8ca6f3_l3.png)
Par hypothèse, tout vecteur de ![]() est combinaison linéaire de
est combinaison linéaire de ![]() Autrement dit, la famille
Autrement dit, la famille ![]() est génératrice de
est génératrice de ![]() Mais comme
Mais comme ![]() c’est en fait une base de
c’est en fait une base de ![]()
En remplaçant ![]() par
par ![]() on obtient pour tout
on obtient pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[e_{j}=\sum_{i=1}^{n}\left(e_{j}\mid e_{i}\right)e_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-05749fa068c3a34e9055cef454825daa_l3.png)
![Rendered by QuickLaTeX.com \[\left(\left\Vert e_{j}\right\Vert ^{2}-1\right)e_{j}+\sum_{{1\leqslant i\leqslant n\atop i\neq j}}\left(e_{j}\mid e_{i}\right)e_{i}=0_{E}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b58496b407d25d4f9098ab7cc8eecfbe_l3.png)
![]()
Remarque
Dans la proposition, on a supposé que ![]() était de dimension
était de dimension ![]() et que la famille était constituée de
et que la famille était constituée de ![]() vecteurs … le même entier n. Sans cette hypothèse, on peut toujours affirmer que
vecteurs … le même entier n. Sans cette hypothèse, on peut toujours affirmer que ![]() est génératrice de
est génératrice de ![]() (et donc que
(et donc que ![]() est de dimension finie), mais
est de dimension finie), mais ![]() n’a aucune raison d’être libre. Un exemple de cette situation est obtenu en prenant
n’a aucune raison d’être libre. Un exemple de cette situation est obtenu en prenant ![]() le produit scalaire étant alors simplement la multiplication des nombres réels. Si l’on pose :
le produit scalaire étant alors simplement la multiplication des nombres réels. Si l’on pose :
![]()
![Rendered by QuickLaTeX.com \[x=\left(x\cdot\dfrac{1}{2}\right)\dfrac{1}{2}+\left(x\cdot\dfrac{\sqrt{3}}{2}\right)\dfrac{\sqrt{3}}{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-543ed66049a30650a1cd2e9af7a3f012_l3.png)
Ajoutons qu’on a aussi, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[x^{2}=\left(x\cdot\dfrac{1}{2}\right)^{2}+\left(x\cdot\dfrac{\sqrt{3}}{2}\right)^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ec9e0d5ff77d900459bc38866890a3f3_l3.png)
2 – Réciproque (B) sans hypothèse de dimension
Proposition
Soient ![]() un EPHR (aucune hypothèse de dimension) et
un EPHR (aucune hypothèse de dimension) et ![]() une famille de vecteurs de
une famille de vecteurs de ![]() On suppose que :
On suppose que :
![Rendered by QuickLaTeX.com \[\forall x\in E,\,\left\Vert x\right\Vert ^{2}=\sum_{i=1}^{n}\,\left(x\mid e_{i}\right)^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-64dd39bed32e0f4f7c2f40c071f75452_l3.png)
![]()
Alors ![]() est une BON de
est une BON de ![]()
Soit ![]() Par hypothèse :
Par hypothèse :
![Rendered by QuickLaTeX.com \[\left\Vert e_{j}\right\Vert ^{2}=\sum_{i=1}^{n}\,\left(e_{j}\mid e_{i}\right)^{2}=\left\Vert e_{j}\right\Vert ^{4}+\sum_{{1\leqslant i\leqslant n\atop i\neq j}}\,\left(e_{j}\mid e_{i}\right)^{2}\geqslant\left\Vert e_{j}\right\Vert ^{4}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-02cd2f609335148b6c6ca68146055458_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{{1\leqslant i\leqslant n\atop i\neq j}}\,\left(e_{j}\mid e_{i}\right)^{2}=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6773226006540848e45de544e9a19ea3_l3.png)
La famille ![]() est donc orthonormale (et, en particulier, libre).
est donc orthonormale (et, en particulier, libre).
On peut montrer qu’elle est aussi génératrice de ![]() de deux manières :
de deux manières :
Méthode 1
Notons ![]() le sev de
le sev de ![]() engendré par
engendré par ![]() Pour tout
Pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\left\Vert x\right\Vert ^{2}=\sum_{i=1}^{n}\,\left(x\mid e_{i}\right)^{2}=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1b8e7163b6dee3719916afc03066e230_l3.png)
Méthode 2
Soit ![]() On souhaite montrer que
On souhaite montrer que ![]() est combinaison linéaire de
est combinaison linéaire de ![]() Si tel est le cas, on aura nécessairement
Si tel est le cas, on aura nécessairement 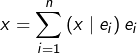 puisque
puisque ![]() est une famille orthonormale. Il est donc naturel d’essayer de prouver que le vecteur
est une famille orthonormale. Il est donc naturel d’essayer de prouver que le vecteur 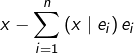 est nul. En développant par bilinéarité et d’après la formule de Pythagore :
est nul. En développant par bilinéarité et d’après la formule de Pythagore :
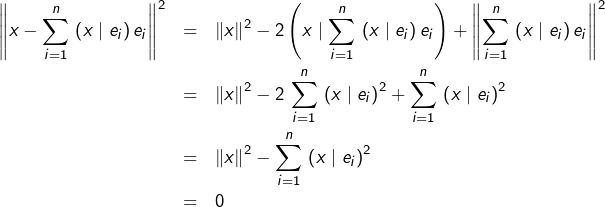
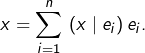 On retrouve le fait que
On retrouve le fait que ➣ En conclusion, ![]() est une BON de
est une BON de ![]()
Remarque
L’espace ![]() n’était pas supposé de dimension finie, mais il s’avère qu’il est de dimension n.
n’était pas supposé de dimension finie, mais il s’avère qu’il est de dimension n.
3 – Réciproque de (B), via matrice de Gram
Proposition
Soient ![]() un EVE de dimension n et
un EVE de dimension n et ![]() une famille de vecteurs de
une famille de vecteurs de ![]() telle que :
telle que :
![Rendered by QuickLaTeX.com \[\forall x\in E,\,\left\Vert x\right\Vert ^{2}=\sum_{i=1}^{n}\,\left(x\mid e_{i}\right)^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-64dd39bed32e0f4f7c2f40c071f75452_l3.png)
On sait déjà, en reprenant par exemple la méthode 1 de la section précédente, que ![]() est une famille génératrice et donc une base de
est une famille génératrice et donc une base de ![]() Introduisons la matrice :
Introduisons la matrice :
![]()
En utilisant une formule de polarisation, on voit que pour tout ![]() :
:
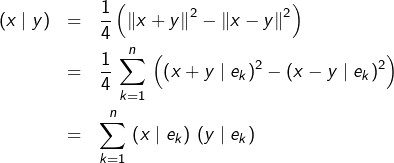
![Rendered by QuickLaTeX.com \[\forall\left(i,j\right)\in\left\llbracket 1,n\right\rrbracket ^{2},\;\left(e_{i}\mid e_{j}\right)=\sum_{k=1}^{n}\,\left(e_{i}\mid e_{k}\right)\,\left(e_{j}\mid e_{k}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-29e929d537ef88ddb4211497d07786f4_l3.png)
Soit donc ![]() tel que
tel que ![]() c’est-à-dire tel que :
c’est-à-dire tel que :
![Rendered by QuickLaTeX.com \[\forall i\in\left\llbracket 1,n\right\rrbracket ,\thinspace\sum_{j=1}^{n}\left(e_{i}\mid e_{j}\right)x_{j}=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-216c7e826d26ac579fc2c624b16aa862_l3.png)
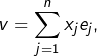 cette condition devient :
cette condition devient : ![]()
Remarque
Autre point de vue : ![]() est la matrice de Gram associée à
est la matrice de Gram associée à ![]() qui est une famille libre. Donc
qui est une famille libre. Donc ![]() est (symétrique) définie positive et, en particulier, inversible.
est (symétrique) définie positive et, en particulier, inversible.
4 – Réciproque de (B), via Cauchy-Schwarz
Proposition
Soient ![]() un EVE de dimension n et
un EVE de dimension n et ![]() une famille de vecteurs de
une famille de vecteurs de ![]() telle que :
telle que :
![Rendered by QuickLaTeX.com \[\forall x\in E,\,\left\Vert x\right\Vert ^{2}=\sum_{i=1}^{n}\,\left(x\mid e_{i}\right)^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-64dd39bed32e0f4f7c2f40c071f75452_l3.png)
… mais par un autre chemin.
Le démarrage de la preuve est le même que précedemment : la famille ![]() est nécessairement une base de
est nécessairement une base de ![]() puisque d’une part, l’orthogonal du sous-espace qu’elle engendre est nul et, d’autre part, elle comporte
puisque d’une part, l’orthogonal du sous-espace qu’elle engendre est nul et, d’autre part, elle comporte ![]() vecteurs avec
vecteurs avec ![]()
Ensuite, comme au début de la section 2, on voit que pour tout ![]() :
: ![]()
Il reste à prouver les inégalités en sens inverse, pour conclure (comme au début de la section 2) que ![]() est une BON de
est une BON de ![]()
Une bonne idée est de faire intervenir l’inégalité de Cauchy-Schwarz (ICS). Rappelons que, pour tout couple ![]() de vecteurs de
de vecteurs de ![]() :
:
![]()
![]()
Or l’existence d’un tel ![]() est assurée : il suffit de considérer l’hyperplan
est assurée : il suffit de considérer l’hyperplan ![]() et de choisir
et de choisir ![]() non nul dans la droite vectorielle
non nul dans la droite vectorielle ![]()


Bonjour Monsieur,
Merci pour ce bel article, qui peut-être ouvrira une séquence estivale 🙂
Bien à vous,
Fabrice