Les repunits sont les entiers naturels dont l’écriture décimale ne comporte que le chiffre ‘1’.
On note ![]() l’ensemble des repunits :
l’ensemble des repunits :
![]()
Déterminer quels sont les polynômes ![]() à coefficients réels tels que :
à coefficients réels tels que :
![]()
Une solution est disponible ici
Les repunits sont les entiers naturels dont l’écriture décimale ne comporte que le chiffre ‘1’.
On note ![]() l’ensemble des repunits :
l’ensemble des repunits :
![]()
Déterminer quels sont les polynômes ![]() à coefficients réels tels que :
à coefficients réels tels que :
![]()
Une solution est disponible ici
Avec l’étudiant du MIT, nous pensons avoir trouvé :
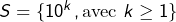
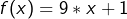
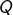 tq
tq 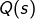 soit dans
soit dans 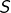 par ex
par ex 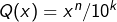 avec
avec 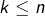
Un polynôme
En appliquant les composées on trouve
ceci car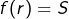 pour tout
pour tout 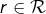 et donc
et donc 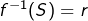
On vérifie pour tout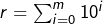 qu’on insère dans
qu’on insère dans 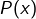 et on trouve un nombre fait d’une succession de chiffres de 9 divisée par 9 donne donc un élément de
et on trouve un nombre fait d’une succession de chiffres de 9 divisée par 9 donne donc un élément de 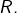
Celui là me semble bien compliqué… j’ai mis un étudiant du MIT sur le coup…. je n’arrive pas à décoller au delà de la décomposition de en fonction des puissances de 10 ou bien de
en fonction des puissances de 10 ou bien de 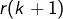 comparé à
comparé à 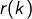 … je suppose bien entendu que
… je suppose bien entendu que 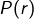 puisse être n’importe quel nombre de
puisse être n’importe quel nombre de 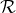 et
et  étant un quelconque nombre de
étant un quelconque nombre de 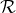 . Les deux étant différents. De même, P est un élément de
. Les deux étant différents. De même, P est un élément de ![Rendered by QuickLaTeX.com \mathbb{R}_n[X]](https://math-os.com/wp-content/ql-cache/quicklatex.com-87e0c961f301bc0d2a500f536a0e94b5_l3.png)