Solution pour le challenge 36
Montrons que, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\boxed{\left|x_{n}-y_{n}\right|\leqslant\frac{1}{1-k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-722c09ca435d99e6657a0979fbf9f1f5_l3.png)
Cette majoration est vraie pour ![]() puisque
puisque ![]()
Supposons-la vraie pour un certain ![]()
Alors d’une part :
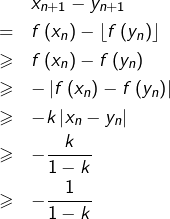
et d’autre part :
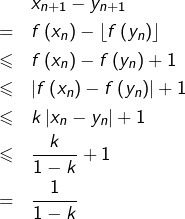
Ainsi :
![]()
comme souhaité.
Maintenant, si l’on remplace l’hypothèse ![]() par l’hypothèse
par l’hypothèse ![]() alors l’écart
alors l’écart ![]() n’est pas borné en général.
n’est pas borné en général.
Considérons par exemple :
![]()
La suite définie par :
![]()
diverge vers ![]() tandis que la suite définie par :
tandis que la suite définie par :
![]()
est constante !
Pour consulter l’énoncé, c’est ici


Excellent. Je comprends à présent d’où vient le choix de la borne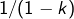 . Cependant, cela demande une une intuition mathématique.
. Cependant, cela demande une une intuition mathématique.
Comment définit-on la borne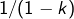 ?
?
N’est-il pas correct de dire que soit que
soit que 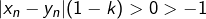 d’où
d’où 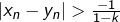 ?
?
Le second membre de l’égalité étant négatif donc toujours inférieur à un nombre positif ?
Resterait alors à prouver que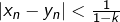 par récurrence comme proposé dans la solution ?
par récurrence comme proposé dans la solution ?
Attention, toutes les inégalités qui interviennent ici sont larges. est évidente et ne mérite aucune justification. En outre, elle n’apporte rien d’utile…
est évidente et ne mérite aucune justification. En outre, elle n’apporte rien d’utile…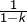 .
.
L’inégalité
Ce que je perçois dans votre commentaire, c’est la question de savoir comment apparaît « naturellement » le majorant
Pour autant que je me souvienne, j’avais initialement obtenu (voir détail dans le corrigé) :
et je m’étais dit que si la suite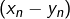 est effectivement majorée (en valeur absolue) par une constante
est effectivement majorée (en valeur absolue) par une constante 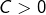 , on devrait avoir l’égalité
, on devrait avoir l’égalité 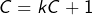 , ce qui conduit tout droit à
, ce qui conduit tout droit à 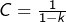 .
.
J’ai pu ensuite prouver que cette borne convient bien.