
Prouver qu’un espace vectoriel est la somme directe de deux (ou plusieurs) sous-espaces est une question omniprésente dans le programme d’algèbre linéaire des deux premières années d’enseignement supérieur scientifique. Elle se traite généralement en raisonnant par analyse-synthèse.
Cet article tâchera de faire le point sur cette question, en partant de zéro (ou presque).
1 – Quelques rappels de cours
Dans ce qui suit, ![]() et
et ![]() désignent respectivement un corps et un
désignent respectivement un corps et un ![]() espace vectoriel.
espace vectoriel.
Le plus souvent, ![]() ou
ou ![]() Plus rarement,
Plus rarement, ![]() ou
ou ![]() (avec
(avec ![]() premier).
premier).
Définition 1
Etant donnés deux sous-espaces vectoriels ![]() et
et ![]() de
de ![]() , on note :
, on note :
![]()
On dit que ![]() est la somme des deux sous-espaces
est la somme des deux sous-espaces ![]() et
et ![]() .
.
On vérifie aisément que ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() .
.

Il ne faut pas confondre ![]() avec
avec ![]() qui, en général, n’est pas un sous-espace vectoriel. Il est cependant facile de voir que
qui, en général, n’est pas un sous-espace vectoriel. Il est cependant facile de voir que ![]() est le sous-espace engendré par
est le sous-espace engendré par ![]() (preuve en annexe).
(preuve en annexe).
Comme le montre l’exemple qui suit, il faut s’attendre à ce qu’un vecteur ![]() puisse généralement s’exprimer de plusieurs manières sous la forme
puisse généralement s’exprimer de plusieurs manières sous la forme ![]() avec
avec ![]() et
et ![]() .
.
Exemple
Considèrons le ![]() espace vectoriel
espace vectoriel ![]() et ses deux sous-espaces :
et ses deux sous-espaces :
![]()
![]()
On constate que, pour tout ![]() :
:
![]()
Ceci nous conduit naturellement à la définition suivante :
Définition 2
On conserve les notations introduites plus haut.
La somme ![]() est dite directe lorsque tout vecteur
est dite directe lorsque tout vecteur ![]() peut s’exprimer d’une seule façon sous la forme
peut s’exprimer d’une seule façon sous la forme ![]() avec
avec ![]() et
et ![]() .
.
On note alors ![]() .
.

Il faut bien voir que ![]() désigne exactement le même objet mathématique que
désigne exactement le même objet mathématique que ![]() , mais avec l’information supplémentaire ( 🙂 jeu de mots) indiquée dans la définition ci-dessus.
, mais avec l’information supplémentaire ( 🙂 jeu de mots) indiquée dans la définition ci-dessus.
Proposition (caractérisation d’une somme directe)
Etant donnés deux sous-espaces ![]() et
et ![]() de
de ![]() , les trois assertions suivantes sont équivalentes :
, les trois assertions suivantes sont équivalentes :
- La somme
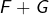 est directe
est directe 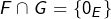
- Pour tout
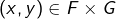 , si
, si 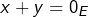 alors
alors 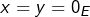
Preuve (cliquer pour déplier / replier)
![]()
Si ![]() , alors
, alors ![]() peut s’exprimer comme la somme d’un vecteur de
peut s’exprimer comme la somme d’un vecteur de ![]() et d’un vecteur de
et d’un vecteur de ![]() comme ceci :
comme ceci :
![]()
![]()
![]()
Soit ![]() tel que
tel que ![]() . On observe que :
. On observe que :
![]()
Il en résulte (d’après (2)) que ![]() .
.
![]()
Soient ![]() et
et ![]() tels que
tels que ![]() .
.
Alors ![]() et comme
et comme ![]() et
et ![]() , il résulte de l’hypothèse (3) que
, il résulte de l’hypothèse (3) que ![]() .
.
Moralité : ![]() ,
, ![]() et l’on a prouvé que la somme
et l’on a prouvé que la somme ![]() est directe.
est directe.
Lorsque deux sous-espaces ![]() et
et ![]() de
de ![]() sont en somme directe, il se peut que cette somme directe soit égale à
sont en somme directe, il se peut que cette somme directe soit égale à ![]() tout entier … ou pas !
tout entier … ou pas !
Définition 3
Deux sous-espace ![]() et
et ![]() de
de ![]() sont dits supplémentaires lorsque :
sont dits supplémentaires lorsque :
![]()
A priori, la preuve d’une égalité du type ![]() doit comporter trois points :
doit comporter trois points :
- Point 0 : prouver que
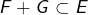 .
. - Point 1 : prouver que
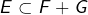 .
. - Point 2 : prouver que la somme
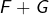 est directe.
est directe.
Mais le point 0 est sans objet ! En effet, l’inclusion ![]() est évidente puisque
est évidente puisque ![]() sont des sous-espaces de
sont des sous-espaces de ![]() ,
,
Il ne reste donc que deux points, le second pouvant être reformulé grâce à la proposition démontrée plus haut :
- Point 1 : prouver que
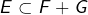 .
. - Point 2 : prouver que
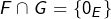 .
.
Le premier point soulève généralement une difficulté spécifique …
On doit en effet se donner un vecteur quelconque ![]() et prouver l’existence de vecteurs
et prouver l’existence de vecteurs ![]() et
et ![]() tels que
tels que ![]() . Mais selon le contexte, il peut ne pas être évident d’aller dénicher deux tels vecteurs
. Mais selon le contexte, il peut ne pas être évident d’aller dénicher deux tels vecteurs ![]() et
et ![]() …
…
Cependant, puisqu’au final il doit exister (pour un ![]() donné) un unique couple
donné) un unique couple ![]() vérifiant
vérifiant ![]() , il doit y avoir un moyen de lui mettre la main dessus sans avoir à jouer aux devinettes !
, il doit y avoir un moyen de lui mettre la main dessus sans avoir à jouer aux devinettes !
Ce moyen est un mode de raisonnement très courant, que nous allons maintenant décrire : le raisonnement par analyse-synthèse.
2 – Principe de preuve par analyse-synthèse
Afin de déterminer les solutions d’un certain problème, on procède de la manière suivante …
Dans un premier temps, on cherche des conditions nécessairement vérifiées par une éventuelle solution.
Si ces conditions sont suffisamment contraignantes, on débouche sur un ensemble assez petit (peut-être fini) de solutions possibles (ou « candidates ») … Cette première partie est appelée « l’analyse » ou « la recherche d’une condition nécessaire ».
Mais attention, rien ne dit à ce stade que ces solutions possibles sont des solutions effectives ! Il se pourrait même que le problème en question ne possède aucune solution.
Pour le savoir, on doit examiner les solutions candidates et déterminer, pour chacune d’elles, s’il s’agit d’une solution effective ou bien si elle doit être écartée. Cette seconde partie est appelée « la synthèse » ou « la recherche d’une condition suffisante ».
Remarque
Si les termes « condition nécessaire » et « condition suffisante » vous paraissent confus, le remède est simple ! Allez donc jeter un coup d’œil à cet article de vulgarisation.
Pour caricaturer le raisonnement par analyse-synthèse, il m’arrive de raconter l’exemple (farfelu) suivant à mes étudiants : imaginez qu’on vous demande de prouver l’existence, dans votre appartement, d’une canette de bière bien fraîche !
Une approche pas très futée consisterait à visiter systématiquement tout l’appartement : l’entrée, le séjour, les chambres à coucher, la salle de bain, etc … jusqu’à ce que vous mettiez la main sur cette fameuse canette.
Il semble judicieux de procéder autrement : si votre appartement abrite effectivement une canette de bière bien fraîche, alors celle-ci doit nécessairement se trouver au réfrigérateur (analyse).
Maintenant, il suffit de filer tout droit dans la cuisine, d’ouvrir la porte du frigo et … de trouver la canette qui nous y attend bien sagement (synthèse).
Nous allons appliquer ce mode de raisonnement au problème particulier qui nous intéresse, à savoir : établir une égalité du type ![]() .
.
Analyse
Donnons-nous un vecteur ![]() et supposons qu’il existe des vecteurs
et supposons qu’il existe des vecteurs ![]() et
et ![]() tels que
tels que ![]() .
.
En profitant du contexte (voir exemples à la section 3 ci-dessous), il est possible de montrer que ![]() et
et ![]() sont déterminés de façon unique en fonction de
sont déterminés de façon unique en fonction de ![]() .
.
Synthèse
Si ![]() et
et ![]() sont définis par les formules obtenues à la fin de la partie « analyse », on doit vérifier que :
sont définis par les formules obtenues à la fin de la partie « analyse », on doit vérifier que :
Afin d’illustrer cela, détaillons quelques exemples.
3 – Six exemples détaillés
Exemple 1
Considérons les vecteurs de ![]() suivants :
suivants :
![]()
![]()
Preuve (cliquer pour déplier / replier)
Raisonnons par analyse-synthèse.
Soit ![]() . Supposons qu’il existe
. Supposons qu’il existe ![]() et
et ![]() tels que :
tels que :
![]()
![]()
![Rendered by QuickLaTeX.com \[\left\{\begin{matrix}a & = & \dfrac{3x+y}{7}\\\\b & = & d\frac{x-2y}{7}\end{matrix}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0db7c2a3b6f8a39c38d8f0ae0774b360_l3.png)
Réciproquement, si ![]() et
et ![]() sont ainsi définis, on vérifie facilement que :
sont ainsi définis, on vérifie facilement que :
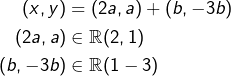
Finalement :
![]()
Plus généralement, si ![]() et
et ![]() sont deux vecteurs non colinéaires d’un
sont deux vecteurs non colinéaires d’un ![]() espace vectoriel
espace vectoriel ![]() de dimension 2, alors :
de dimension 2, alors :
![]()
Encore plus généralement, si ![]() est une famille libre de vecteurs d’un
est une famille libre de vecteurs d’un ![]() espace vectoriel
espace vectoriel ![]() de dimension
de dimension ![]() alors :
alors :
![Rendered by QuickLaTeX.com \[E=\bigoplus_{i=1}^n\mathbb{K}e_i\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6a29e93d3d668846bc48107f4f31c578_l3.png)
Exemple 2
Soient ![]() et
et ![]() . Alors :
. Alors :
![]()
Preuve (cliquer pour déplier / replier)
Raisonnons par analyse-synthèse.
Soit ![]() . Supposons qu’il existe
. Supposons qu’il existe ![]() et
et ![]() tels que :
tels que :
![]()
![]()
![Rendered by QuickLaTeX.com \[\left\{\begin{matrix}x & = & 2\lambda+a & \qquad(1)\\y & = & \lambda+b & \qquad(2)\\z & = & -\lambda+a+2b & \qquad(3)\end{matrix}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-177bacac54aae7b98475398afbb8114c_l3.png)
Alors, en effectuant la combinaison ![]() :
:
![Rendered by QuickLaTeX.com \[\lambda=\boxed{\frac{x+2y-z}{5}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-994101e1db7ead7525ad77b8b5bedd71_l3.png)
![Rendered by QuickLaTeX.com \[a=x-2\lambda=x-\frac{2x+4y-2z}{5}=\boxed{\frac{3x-4y+2z}{5}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-768ccc2571f026c3db84d9b381e256bb_l3.png)
![Rendered by QuickLaTeX.com \[b=y-\lambda=y-\frac{x+2y-z}{5}=\boxed{\frac{-x+3y+z}{5}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7252ab50eca68dbc6ccbf7b825162dec_l3.png)
Réciproquement, si ![]() ,
, ![]() et
et ![]() sont respectivement définis par les formules encadrées, alors :
sont respectivement définis par les formules encadrées, alors :
![Rendered by QuickLaTeX.com \[\left\{\begin{matrix}X=(2\lambda,\lambda,-\lambda) & \in & \mathbb{R}(2,1,-1)\\\\Y=\displaystyle{(\frac{3x-4y+2z}{5},\frac{-x+3y+z}{5},\frac{x+2y+4z}{5})} & \in & H\\\\X+Y & = & (x,y,z)\end{matrix}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1f011422b4512b56007d622295dadce7_l3.png)
Finalement :
![]()
Plus généralement, si ![]() est un hyperplan de
est un hyperplan de ![]() (c’est-à-dire, lorsque
(c’est-à-dire, lorsque ![]() est de dimension
est de dimension ![]() , un sous-espace de dimension
, un sous-espace de dimension ![]() et, en toute généralité, le noyau d’une forme linéaire non nulle) et si
et, en toute généralité, le noyau d’une forme linéaire non nulle) et si ![]() , alors
, alors ![]() .
.
Preuve (cliquer pour déplier / replier)
Soit ![]() un
un ![]() -espace vectoriel et soit
-espace vectoriel et soit ![]() une forme linéaire sur
une forme linéaire sur ![]() (c’est-à-dire une application linéaire de
(c’est-à-dire une application linéaire de ![]() dans
dans ![]() ).
).
Supposons ![]() non nulle et notons
non nulle et notons ![]() son noyau (qui est donc strictement contenu dans
son noyau (qui est donc strictement contenu dans ![]() ).
).
Soit encore ![]() ; montrons que
; montrons que
![]()
Pour cela, raisonnons, encore et toujours, par analyse-synthèse.
Etant donné ![]() , supposons qu’il existe
, supposons qu’il existe ![]() et
et ![]() tels que :
tels que :
![]()
On appliquant ![]() , on voit que :
, on voit que :
![]()
![]()
![]()
Réciproquement, si ![]() et
et ![]() sont ainsi définis, alors d’évidence
sont ainsi définis, alors d’évidence ![]() et de plus :
et de plus :
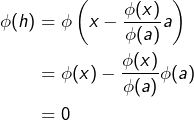
Exemple 3
Notons ![]() le
le ![]() espace vectoriel des applications de
espace vectoriel des applications de ![]() dans
dans ![]() et considérons les deux sous-ensembles suivants :
et considérons les deux sous-ensembles suivants :
![]() désigne l’ensemble des applications
désigne l’ensemble des applications ![]() qui sont paires, c’est-à-dire telles que :
qui sont paires, c’est-à-dire telles que :
![]()
![]() désigne l’ensemble des applications
désigne l’ensemble des applications ![]() qui sont impaires, c’est-à-dire telles que :
qui sont impaires, c’est-à-dire telles que :
![]()
Avec ces notations, ![]() et
et ![]() sont des sous-espaces vectoriels de
sont des sous-espaces vectoriels de ![]() et de plus :
et de plus :
![]()
Preuve (cliquer pour déplier / replier)
Raisonnons par analyse-synthèse.
Soit ![]() . Supposons qu’il existe
. Supposons qu’il existe ![]() et
et ![]() telles que
telles que ![]() .
.
Alors, pour tout ![]() :
:
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{p(x)=\frac{f(x)+f(-x)}{2}}\qquad\text{et}\qquad\boxed{i(x)=\frac{f(x)-f(-x)}{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e1e3ae9c3dceeb62f3cea5ddebc4c789_l3.png)
Réciproquement, si ![]() et
et ![]() sont ainsi définies, alors on voit immédiatement que
sont ainsi définies, alors on voit immédiatement que ![]() est paire, que
est paire, que ![]() est impaire et que
est impaire et que ![]() .
.
En conclusion, toute application ![]() peut s’écrire, de manière unique, comme la somme d’une application paire et d’une application impaire. Autrement dit :
peut s’écrire, de manière unique, comme la somme d’une application paire et d’une application impaire. Autrement dit :
![]()
En particulier, la fonction exponentielle se décompose en ses parties paire et impaire, respectivement définies par :
![]()
La première de ces deux fonctions est appelée « cosinus hyperbolique » et la seconde « sinus hyperbolique ». Elles sont traditionnellement notée cosh et sinh (notation internationale … en France, on est habitué aux notations ch et sh).
Sans entamer une trop longue digression à ce sujet, on peut préciser que le qualificatif d’hyperbolique provient du fait que les deux branches de l’hyperbole d’équation ![]() admettent les représentations paramétriques suivantes :
admettent les représentations paramétriques suivantes :
![]()
![]()
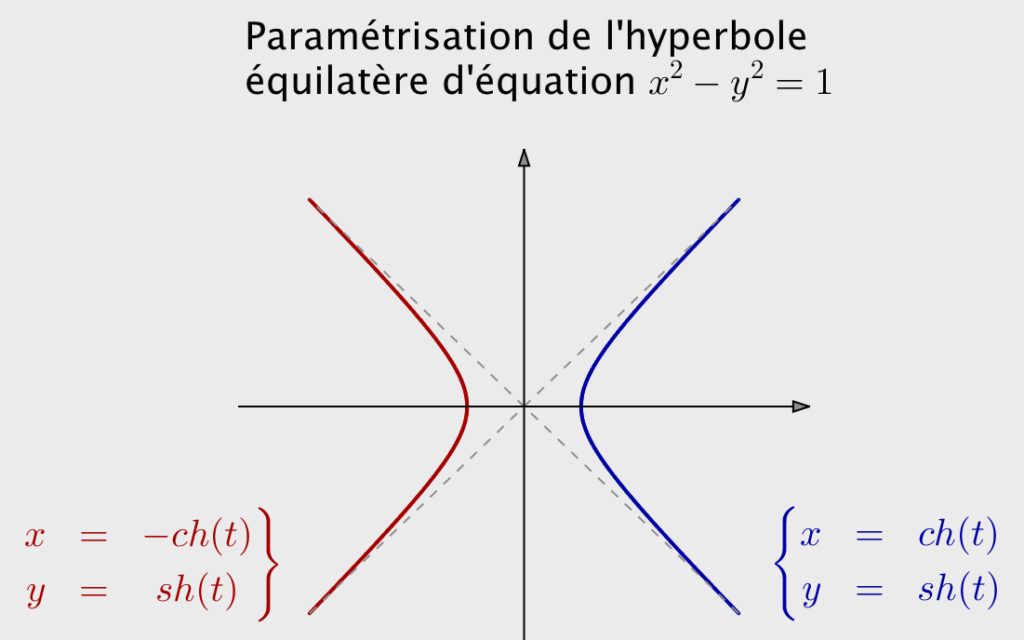
Ceci est à rapprocher du fait que le cercle unité admet la célèbre représentation paramétrique :
![]()
ce qui explique la terminologie de trigonométrie circulaire.
Exemple 4
Soit ![]() un
un ![]() espace vectoriel et soit
espace vectoriel et soit ![]() un endomorphisme de
un endomorphisme de ![]() tel que
tel que ![]() .
.
Alors :
![]()
Preuve (cliquer pour déplier / replier)
Raisonnons par analyse-synthèse.
Soit ![]() . Supposons qu’il existe
. Supposons qu’il existe ![]() et
et ![]() tels que :
tels que :
![]()
En appliquant ![]() à chaque membre de cette égalité, il vient :
à chaque membre de cette égalité, il vient :
![]()
![]()
![]()
![]()
![]()
On a bien prouvé que :
![]()
Cet exemple est fondamental. Les endomorphismes ![]() vérifiant
vérifiant ![]() (ce qu’on peut aussi noter
(ce qu’on peut aussi noter ![]() ) sont appelés projecteurs et jouent un rôle central en algèbre linéaire et en géométrie.
) sont appelés projecteurs et jouent un rôle central en algèbre linéaire et en géométrie.
Précisons que si ![]() est un projecteur, son sous-espace invariant
est un projecteur, son sous-espace invariant ![]() est confondu avec son image. Sauriez-vous établir cela ? Réponse en annexe.
est confondu avec son image. Sauriez-vous établir cela ? Réponse en annexe.
Aux projecteurs sont associés d’autres endomorphismes d’usage fréquent : les symétries. Ce sont les ![]() vérifiant
vérifiant ![]() . Sauriez-vous prouver que si
. Sauriez-vous prouver que si ![]() vérifie cette condition, alors
vérifie cette condition, alors ![]() ? Réponse en annexe également …
? Réponse en annexe également …
Exemple 5
Soit ![]() un
un ![]() espace vectoriel et soit
espace vectoriel et soit ![]() un endomorphisme tel que
un endomorphisme tel que ![]() . Alors :
. Alors :
![]()
Détail des calculs (cliquer pour déplier / replier)
Soit ![]() . Supposons qu’il existe
. Supposons qu’il existe ![]() et
et ![]() tels que :
tels que :
![]()
![]()
![]()
![]()
Réciproquement, si ![]() et
et ![]() sont ainsi définis, alors on constate que :
sont ainsi définis, alors on constate que :
ce qui montre déjà que ![]() et
et ![]() . En outre, il est clair que
. En outre, il est clair que ![]() . Ceci termine la preuve.
. Ceci termine la preuve.
Cet exemple et le précédent sont deux cas particuliers d’un résultat général, connu sous le nom de lemme de décomposition des noyaux. Pour en savoir plus à ce sujet, on pourra consulter cette vidéo.
Exemple 6
Considérons l’espace ![]() des applications de classe
des applications de classe ![]() de
de ![]() dans
dans ![]() ainsi qu’un entier
ainsi qu’un entier ![]() .
.
Notons alors :
![]()
![]()
ainsi que :
![]()
Alors : ![]() .
.
Preuve (cliquer pour déplier / replier)
Il se trouve que ![]() est (d’évidence) un sous-espace de dimension finie de
est (d’évidence) un sous-espace de dimension finie de ![]() et que
et que ![]() n’est autre que son orthogonal relativement au produit scalaire défini par :
n’est autre que son orthogonal relativement au produit scalaire défini par :
![]()
La conclusion est alors conséquence d’un résultat général, à savoir que si ![]() est un sous-espace de dimension finie d’un espace préhilbertien réel
est un sous-espace de dimension finie d’un espace préhilbertien réel ![]() , alors
, alors ![]() . Pour aller plus loin sur ce terrain, on pourra consulter cet article.
. Pour aller plus loin sur ce terrain, on pourra consulter cet article.
4 – L’astuce de la dimension finie
Soient, à nouveau, un ![]() espace vectoriel
espace vectoriel ![]() et deux sous-espaces
et deux sous-espaces ![]() et
et ![]() de
de ![]() .
.
Si ![]() est de dimension finie et si l’on veut prouver que
est de dimension finie et si l’on veut prouver que ![]() , alors il suffit de vérifier que :
, alors il suffit de vérifier que :
![]()
![]()
![]()
![]()
ou bien de vérifier que :
![]()
![]()
![]()
![]()
➥ En effet, sous les hypothèses ![]() et
et ![]() :
:
![]()
➥ Et sous les hypothèses ![]() et
et ![]() , on voit déjà (avec
, on voit déjà (avec ![]() ) que
) que ![]() , puis d’après la formule de Grassmann :
, puis d’après la formule de Grassmann :
![]()
Pour l’essentiel, cette méthode nous épargne le calcul explicite de la décomposition d’un vecteur quelconque de ![]() en la somme d’un vecteur de
en la somme d’un vecteur de ![]() et d’un vecteur de
et d’un vecteur de ![]() .
.
Ceci est un avantage dans la mesure où la dose de calcul est allégée … mais cela peut constituer un inconvénient si l’on a besoin de connaître explicitement cette fameuse décomposition (par exemple, pour déterminer l’expression analytique d’un projecteur une d’une symétrie).
Donnons un exemple d’utilisation de cette idée…
Exemple
Considérons un ![]() espace vectoriel de dimension finie
espace vectoriel de dimension finie ![]() et un endomorphisme
et un endomorphisme ![]() de
de ![]() .
.
On suppose qu’il existe ![]() tel que :
tel que :
- (1)
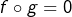
- (2)
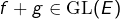
Montrons que, sous ces hypothèses :
![]()
Preuve (cliquer pour déplier / replier)
L’hypothèse (1) se traduit par l’inclusion ![]() .
.
Il est par ailleurs évident que ![]() .
.
Donc, d’après (2) :
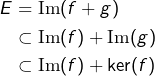
ce qui impose : ![]()
En outre, d’après la formule de Grassmann :
![]()
et donc, en appliquant à ![]() la formule du rang :
la formule du rang :
![]()
![]()
Remarque 1
Les conditions (1) et (2) ci-dessus sont remplies dans le cas où ![]() est un projecteur. En effet, si l’on pose
est un projecteur. En effet, si l’on pose ![]() , alors :
, alors :
- d’une part
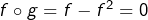
- d’autre part
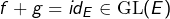
Ceci permet de retrouver l’égalité ![]() qui est bien connue dans ce cas (voir l’exemple 4 ci-dessus).
qui est bien connue dans ce cas (voir l’exemple 4 ci-dessus).
Remarque 2
Les conditions (1) et (2) entraînent que l’image et le noyau de ![]() sont supplémentaires. Cette implication est en fait une équivalence.
sont supplémentaires. Cette implication est en fait une équivalence.
En effet, introduisons le projecteur ![]() sur
sur ![]() et parallèlement à
et parallèlement à ![]() .
.
- D’une part, pour tout
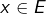 , on a
, on a 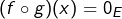 puisque
puisque 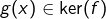 . Ainsi :
. Ainsi : 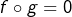 .
. - D’autre part, si
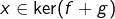 , alors
, alors 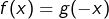 , ce qui montre que
, ce qui montre que 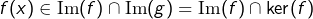 et donc
et donc 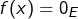 . Mais alors
. Mais alors 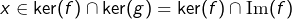 et donc
et donc 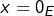 . Ceci prouve que
. Ceci prouve que 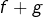 est un endomorphisme injectif et donc un automorphisme de
est un endomorphisme injectif et donc un automorphisme de  .
.
5 – Quelques mots au sujet de 
Bien que ce ne soit pas le thème principal de cet article, on ne pouvait pas laisser sous silence la généralisation naturelle de ce qui précède au cas de plusieurs sous-espaces.
Voici donc, à nouveau, les définitions 1 et 2 données au tout début, mais sous une forme élargie :
Définition
Etant donnés un entier ![]() et des sous-espaces vectoriels
et des sous-espaces vectoriels ![]() de
de ![]() , on note :
, on note :
![Rendered by QuickLaTeX.com \[\sum_{i=1}^nE_i=\left\{\sum_{i=1}^nx_i;\,\forall i\in\llbracket1,n\rrbracket,\,x_i\in E_i\right\}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2fa4d4bea6b78b7b7c34426c53bc8e22_l3.png)
En bon français, cela signifie simplement que ![]() est l’ensemble des vecteurs pouvant s’écrire comme la somme d’un vecteur de
est l’ensemble des vecteurs pouvant s’écrire comme la somme d’un vecteur de ![]() , d’un vecteur de
, d’un vecteur de ![]() , etc …, d’un vecteur de
, etc …, d’un vecteur de ![]() .
.
Cette somme 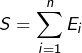 est dite directe lorsque tout vecteur de
est dite directe lorsque tout vecteur de ![]() peut s’écrire d’une seule manière sous cette forme. On note alors
peut s’écrire d’une seule manière sous cette forme. On note alors ![]() au lieu de
au lieu de ![]() .
.
Nous avons vu plus haut une proposition caractérisant les sommes directes de deux sous-espaces. Voici comment on peut la généraliser à un nombre quelconque de sous-espaces :
Proposition
Soient ![]() des sous-espaces vectoriels de
des sous-espaces vectoriels de ![]() .
.
Les assertions suivantes sont équivalentes :
- La somme
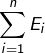 est directe
est directe - Quels que soient les vecteurs
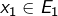 …
… 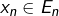 :
:![Rendered by QuickLaTeX.com \[\sum_{i=1}^nx_i=0_E\Rightarrow\forall i\in\llbracket1,n\rrbracket,\,x_i=0_E\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2c60588d254e3bdf14d4bb28a490e111_l3.png)

Une erreur classique consiste à affirmer que la somme des ![]() serait directe si, et seulement si,
serait directe si, et seulement si, 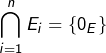 . C’est correct pour
. C’est correct pour ![]() , mais c’est faux dès que
, mais c’est faux dès que ![]() .
.
Par exemple, l’intersection de trois droites vectorielles distinctes de ![]() est réduite à
est réduite à ![]() mais la somme de ces trois droites n’est évidemment pas directe (sans quoi sa dimension serait égale à 3, ce qui est un peu trop pour un sous-espace de
mais la somme de ces trois droites n’est évidemment pas directe (sans quoi sa dimension serait égale à 3, ce qui est un peu trop pour un sous-espace de ![]() ).
).
Donnons un exemple simple et significatif de somme directe de plusieurs sous-espaces.
Exemple : somme directe de sev propres
Soit ![]() un
un ![]() espace vectoriel et soit
espace vectoriel et soit ![]() .
.
Supposons que ![]() (avec
(avec ![]() ) soient des valeurs propres de
) soient des valeurs propres de ![]() , deux à deux distinctes.
, deux à deux distinctes.
Notons, pour tout ![]() :
:
![]()
Alors la somme ![]() est directe.
est directe.
Preuve (cliquer pour déplier / replier)
On procède par récurrence sur le nombre de valeurs propres.
Pour ![]() , il n’y a rien à démontrer.
, il n’y a rien à démontrer.
Supposons la propriété établie pour un certain ![]() et soient alors
et soient alors ![]() des valeurs propres deux à deux distinctes de
des valeurs propres deux à deux distinctes de ![]() .
.
Pour montrer que la somme ![]() est directe, utilisons la caractérisation donnée dans la proposition précédente.
est directe, utilisons la caractérisation donnée dans la proposition précédente.
Soient ![]() , …,
, …, ![]() tels que :
tels que :
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{r+1}x_i=0_E\qquad\left(\spadesuit}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-90f447a8050e014026abd5991a75779b_l3.png)
Appliquons ![]() :
:
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{r+1}\lambda_i\,x_i=0_E\qquad\left(\clubsuit\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-88c0073dda46402d4a0d20e9875fc928_l3.png)
Retranchons à ![]() l’égalité
l’égalité ![]() préalablement multipliée par
préalablement multipliée par ![]() :
:
![Rendered by QuickLaTeX.com \[\sum_{i=1}^r\left(\lambda_i-\lambda_{r+1}\right)x_i=0_E\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-864269c495b4d7a305964698ed7c1b73_l3.png)
L’hypothèse de récurrence permet d’affirmer que :
![]()
![]()

Attention, cette somme directe n’a aucune raison d’être égale à ![]() tout entier !
tout entier !
Cependant, le cas où 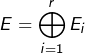 est important, car il existe alors une base de
est important, car il existe alors une base de ![]() (obtenue en concaténant des bases de chacun des
(obtenue en concaténant des bases de chacun des ![]() ) dans laquelle
) dans laquelle ![]() est représenté par une matrice diagonale. On dit, dans ce cas, que l’endomorphisme
est représenté par une matrice diagonale. On dit, dans ce cas, que l’endomorphisme ![]() est diagonalisable.
est diagonalisable.
Annexe
Dans cette section, on détaille les réponses aux questions laissées en suspens plus haut.
Proposition annexe 1
Si ![]() et
et ![]() sont deux sous-espaces vectoriels de
sont deux sous-espaces vectoriels de ![]() , alors :
, alors :
![]()
Preuve (cliquer pour déplier / replier)
Rappelons au préalable que si ![]() , on désigne par
, on désigne par ![]() l’ensemble des combinaisons linéaires de vecteurs de
l’ensemble des combinaisons linéaires de vecteurs de ![]() . Il s’agit d’un sous-espace de
. Il s’agit d’un sous-espace de ![]() , qui est aussi l’intersection de la famille des sous-espaces contenant
, qui est aussi l’intersection de la famille des sous-espaces contenant ![]() .
.
En outre, tout sous-espace de ![]() contenant
contenant ![]() contient nécessairement
contient nécessairement ![]() .
.
Cela dit …
Il est clair que ![]() et que
et que ![]() . Ainsi
. Ainsi ![]() et comme
et comme ![]() est un sev de
est un sev de ![]() , alors
, alors ![]() .
.
Par ailleurs, si ![]() , alors il existe
, alors il existe ![]() et
et ![]() tels que
tels que ![]() , ce qui montre que
, ce qui montre que ![]() .
.
Proposition annexe 2
Si ![]() est un projecteur, alors son sous-espace invariant coïncide avec son image.
est un projecteur, alors son sous-espace invariant coïncide avec son image.
Preuve (cliquer pour déplier / replier)
Si ![]() , alors
, alors ![]() , et donc
, et donc ![]() . Ceci prouve que
. Ceci prouve que ![]() . Noter que cette inclusion reste valable pour n’importe quel endomorphisme !
. Noter que cette inclusion reste valable pour n’importe quel endomorphisme !
Réciproquement, si ![]() , alors il existe
, alors il existe ![]() tel que
tel que ![]() , d’où
, d’où ![]() . Et ceci prouve l’inclusion inverse.
. Et ceci prouve l’inclusion inverse.
Proposition annexe 3
Soit ![]() vérifiant
vérifiant ![]() . Alors :
. Alors :
![]()
Preuve 1 (cliquer pour déplier / replier)
Soit ![]() . Supposons qu’il existe
. Supposons qu’il existe ![]() et
et ![]() tels que
tels que ![]() . En appliquant
. En appliquant ![]() , on obtient
, on obtient ![]() puis, par somme et différence :
puis, par somme et différence :
![Rendered by QuickLaTeX.com \[\left\{\begin{matrix}a & = & \frac12\left(x+s(x)\right)\\\\b & = & \frac12\left(x-s(x)\right) \end{matrix}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-14219b2779a8b0b59f1ac7f3138a6f19_l3.png)
Réciproquement, si ![]() et
et ![]() sont ainsi définis, alors il est immédiat que
sont ainsi définis, alors il est immédiat que ![]() .
.
En outre :
donc ![]() et
et ![]() .
.
Preuve 2 (cliquer pour déplier / replier)
Posons :
![]()
![]()
Autrement dit, ![]() est un projecteur et nous savons que :
est un projecteur et nous savons que :
![]()
Or, il est facile de voir que :
![]()
J’espère avoir contribué, par cet article, à vous rendre les choses plus claires 🙂
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.
