On s’intéresse ici au calcul de l’intégrale impropre :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{I=\int_{0}^{1}\dfrac{\ln\left(t\right)\ln^{2}\left(1-t\right)}{t}\thinspace dt}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d65d8a55a72ecd433a6b2d8827aca65d_l3.png)
Cette question provient de la rubrique Advanced Problems de l’American Mathematical Monthly (1982 – Vol 3 – A6382).
Il arrive parfois qu’une intégrale puisse être calculée explicitement, sans que l’on sache expliciter de primitive de la fonction intégrée. Une des techniques permettant cela est un développement en série, couplé à une intégration terme à terme : s’il s’avère que la série numérique obtenue est connue ou, tout au moins, calculable par une méthode ou une autre, on sera sorti d’affaire !
Un exemple simple de ce scenario est détaillée à la section 1. Il s’agit du calcul de :
![]()
Dans ce qui va suivre, on se permettra, sans autre forme de procès, d’intervertir des séries et des intégrales, ce qui dans l’absolu peut poser problème ! Mais en l’occurrence, il s’agira à chaque fois de l’intégration terme à terme d’une suite de fonctions continues, intégrables et positives sur un intervalle. Il est connu qu’avec de telles hypothèses, l’interversion série / intégrale ne soulève pas de difficulté.
On utilisera par ailleurs la fonction zeta de Riemann (voir cette note du lexique) définie par :
![Rendered by QuickLaTeX.com \[\forall s>1,\thinspace\zeta\left(s\right)=\sum_{n=1}^{+\infty}\dfrac{1}{n^{s}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-db9456b9c1422174db97831c27d1b310_l3.png)
![]()
1 – Un exemple simple
Tout d’abord l’intégrale ![]() ci-dessus est impropre pour chacune des bornes 0 et 1.
ci-dessus est impropre pour chacune des bornes 0 et 1.
Lorsque ![]() tend vers
tend vers ![]() :
:
![]()
![]()
Maintenant que la convergence de l’intégrale ![]() est établie, passons à son calcul. Une piste prometteuse consiste à développer
est établie, passons à son calcul. Une piste prometteuse consiste à développer ![]() en série géométrique. On sait que :
en série géométrique. On sait que :
![Rendered by QuickLaTeX.com \[\forall t\in\left]0,1\right[,\thinspace\dfrac{\ln\left(t\right)}{1-t}=\sum_{n=0}^{+\infty}t^{n}\ln\left(t\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-95c1da18892569e1c945edb3a065ac98_l3.png)
![Rendered by QuickLaTeX.com \[J=\sum_{n=0}^{+\infty}\int_{0}^{1}t^{n}\ln\left(t\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-478ffcd80382ca32247466ee3f7df805_l3.png)
![Rendered by QuickLaTeX.com \[\int_{0}^{1}t^{n}\ln\left(t\right)\thinspace dt=\left[\dfrac{t^{n+1}}{n+1}\ln\left(t\right)\right]_{0}^{1}-\int_{0}^{1}\dfrac{t^{n}}{n+1}\thinspace dt=-\dfrac{1}{\left(n+1\right)^{2}}et\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-53a09b412c8a754779cdf5e8bab4109c_l3.png)
![Rendered by QuickLaTeX.com \[J=-\sum_{n=0}^{+\infty}\dfrac{1}{\left(n+1\right)^{2}}=-\zeta\left(2\right)=\boxed{-\dfrac{\pi^{2}}{6}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5700a1e4155297c2e387b9ad61ac491b_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\forall s\in\left]0,1\right[,\thinspace\ln\left(1-s\right)=-\sum_{n=1}^{+\infty}\dfrac{s^{n}}{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9d6aa9d70e1039024e6edfbe9bad08b9_l3.png)
![Rendered by QuickLaTeX.com \[J=-\int_{0}^{1}\sum_{n=1}^{+\infty}\dfrac{s^{n-1}}{n}\thinspace ds=-\sum_{n=1}^{+\infty}\int_{0}^{1}\dfrac{s^{n-1}}{n}\thinspace ds=-\sum_{n=1}^{+\infty}\dfrac{1}{n^{2}}=-\zeta\left(2\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cfea317c1294fb546c0332f12d811ce3_l3.png)
2 – Une formule due à Euler
On va calculer ici la somme de la série :
![Rendered by QuickLaTeX.com \[\boxed{A=\sum_{n=1}^{+\infty}\dfrac{H_{n}}{n^{3}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fe467b98990ea7fde4aa0605a2380aaf_l3.png)
![Rendered by QuickLaTeX.com \[H_{n}=\sum_{k=1}^{n}\dfrac{1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1b8bbbae3fbf612580193470a1979179_l3.png)
![]()
![Rendered by QuickLaTeX.com \[A=\sum_{n=1}^{+\infty}\left(\dfrac{1}{n^{3}}\int_{0}^{1}\dfrac{1-t^{n}}{1-t}\right)\thinspace dt=\int_{0}^{1}\left(\dfrac{1}{1-t}\sum_{n=1}^{+\infty}\dfrac{1-t^{n}}{n^{3}}\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e38140ecc810319b0a84346096561a9d_l3.png)
Posons alors, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[f\left(t\right)=\sum_{n=1}^{+\infty}\dfrac{t^{n}}{n^{3}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e629b61f60195a2143e5c7d3769bab73_l3.png)
![]()
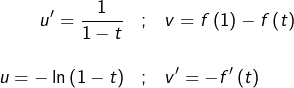
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[t\thinspace f'\left(t\right)=\sum_{n=1}^{+\infty}\dfrac{t^{n}}{n^{2}}\qquad\text{et}\qquad-\dfrac{\ln\left(1-t\right)}{t}=\sum_{n=1}^{+\infty}\dfrac{t^{n-1}}{n}=\dfrac{d}{dt}\left(t\thinspace f'\left(t\right)\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-099e03d54ceb9c82e4d73d2b9acf27d1_l3.png)
![Rendered by QuickLaTeX.com \[A=\left[\dfrac{1}{2}\left(t\thinspace f'\left(t\right)\right)^{2}\right]_{0}^{1}=\dfrac{1}{2}\thinspace f'\left(1\right)^{2}=\dfrac{1}{2}\zeta\left(2\right)^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9407c1081f0860280209304125b7fb0d_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{A=\dfrac{\pi^{4}}{72}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d5f20834b3eea06a77029812b6841bf9_l3.png)
Théorème
Pour tout entier ![]() :
:
![Rendered by QuickLaTeX.com \[\sum_{n=1}^{+\infty}\dfrac{H_{n}}{n^{q}}=\left(1+\dfrac{q}{2}\right)\thinspace\zeta\left(q+1\right)-\dfrac{1}{2}\sum_{k=1}^{q-2}\zeta\left(k+1\right)\thinspace\zeta\left(q-k\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-62fd3b6c1b0bc75f4bbb7ad2bed9c5af_l3.png)
La source principale pour ce résultat est le texte de Leonhard Euler, intitulé « Meditationes circa singulare serierum genus » (ce qu’on peut traduire par « méditations sur un type particulier de série ») et paru en 1776.
Pour ![]() cette formule donne :
cette formule donne :
![Rendered by QuickLaTeX.com \[\sum_{n=1}^{+\infty}\dfrac{H_{n}}{n^{3}}=\dfrac{5}{2}\thinspace\zeta\left(4\right)-\dfrac{1}{2}\thinspace\zeta\left(2\right)^{2}=\dfrac{5}{2}\thinspace\dfrac{\pi^{4}}{90}-\dfrac{1}{2}\left(\dfrac{\pi^{2}}{6}\right)^{2}=\dfrac{\pi^{4}}{72}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c0851182a05e109e9ad06761168415dd_l3.png)
3 – Merci Niels Henrik Abel
On va maintenant se pencher sur le calcul de :
![Rendered by QuickLaTeX.com \[\boxed{B=\sum_{n=1}^{+\infty}\dfrac{H_{n}}{\left(n+1\right)^{3}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d5228d736e0b50f2354d73a972ce424d_l3.png)
![Rendered by QuickLaTeX.com \[A-B=\sum_{n=1}^{+\infty}H_{n}\left(\dfrac{1}{n^{3}}-\dfrac{1}{\left(n+1\right)^{3}}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-14d19a41f97aa1a1482cfe5a91f8baa8_l3.png)
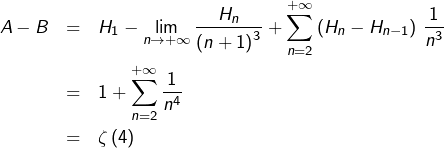
![Rendered by QuickLaTeX.com \[\boxed{B=\dfrac{\pi^{4}}{360}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0e4edd0e85ce78f97bdbd013b2a049af_l3.png)
4 – Calcul de l’intégrale I
On s’attaque pour terminer au calcul de :
![Rendered by QuickLaTeX.com \[\boxed{I=\int_{0}^{1}\dfrac{\ln\left(t\right)\ln^{2}\left(1-t\right)}{t}\thinspace dt}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8ff5bf6e500d5b48665ebab63130f97d_l3.png)
- Lorsque
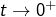 :
:
et![Rendered by QuickLaTeX.com \[\ln\left(t\right)\ln\left(1-t\right)\sim-t\ln\left(t\right)\rightarrow0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-efee08ab7351217196e6dcd1e3195987_l3.png)
d’où :![Rendered by QuickLaTeX.com \[\dfrac{\ln\left(1-t\right)}{t}\rightarrow-1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5e2bae0c6fb01a3388dcbdab7fd0fe79_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\lim_{t\rightarrow0^{+}}\dfrac{\ln\left(t\right)\ln^{2}\left(1-t\right)}{t}=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a107f9e1e23b82ae9704a27d06825831_l3.png)
- Et lorsque
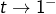 :
:
donc :![Rendered by QuickLaTeX.com \[\ln\left(t\right)\sim t-1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3ddd732ffa845905cba299130def322b_l3.png)
Or, lorsque![Rendered by QuickLaTeX.com \[\dfrac{\ln\left(t\right)\ln^{2}\left(1-t\right)}{t}\sim\ln\left(t\right)\ln^{2}\left(1-t\right)\sim\left(t-1\right)\ln^{2}\left(1-t\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6627ae1f47a6739fe9e289f4de53fa64_l3.png)
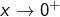 :
:
et donc :![Rendered by QuickLaTeX.com \[x\ln^{2}\left(x\right)=\left[2\sqrt{x}\ln\left(\sqrt{x}\right)\right]^{2}\rightarrow0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fc790ac26a4e5cfb31b74bec92038bd0_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\lim_{t\rightarrow1^{-}}\dfrac{\ln\left(t\right)\ln^{2}\left(1-t\right)}{t}=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a37fd8383cdc73bc9a4e26f8624fa470_l3.png)
On peut développer en série ![]() pour tout
pour tout ![]() en effectuant le produit de Cauchy par elle-même de la série :
en effectuant le produit de Cauchy par elle-même de la série :
![Rendered by QuickLaTeX.com \[-\ln\left(1-t\right)=\sum_{n=1}^{+\infty}\dfrac{t^{n}}{t}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-27d87a9899f0d4817648b17a33527062_l3.png)
![Rendered by QuickLaTeX.com \[\ln^{2}\left(1-t\right)=\sum_{n=2}^{+\infty}\left(\sum_{k=1}^{n-1}\dfrac{1}{k\left(n-k\right)}\right)t^{n}=2\sum_{n=2}^{+\infty}\dfrac{H_{n-1}}{n}t^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-67c8ab37654f5469f9b4899c77b35b47_l3.png)
![Rendered by QuickLaTeX.com \[\int_{0}^{1}\dfrac{\ln\left(t\right)\ln^{2}\left(1-t\right)}{t}\thinspace dt=2\int_{0}^{1}\sum_{n=2}^{+\infty}\dfrac{H_{n-1}}{n}t^{n-1}\ln\left(t\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bef1576b27f341eec3a9d52cff2c304c_l3.png)
![Rendered by QuickLaTeX.com \[\int_{0}^{1}\dfrac{\ln\left(t\right)\ln^{2}\left(1-t\right)}{t}\thinspace dt=-2\sum_{n=2}^{+\infty}\dfrac{H_{n-1}}{n^{3}}=-2\sum_{n=1}^{+\infty}\dfrac{H_{n}}{\left(n+1\right)^{3}}=-2B\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-74165e66e044e0e862f76673c9b0fd6e_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\int_{0}^{1}\dfrac{\ln\left(t\right)\ln^{2}\left(1-t\right)}{t}\thinspace dt=-\dfrac{\pi^{4}}{180}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c1bebb524499d8142c349906e71f09d6_l3.png)
evalf(Int(ln(t){*}ln(1-t)\textasciicircum 2/t,t=0..1),30);-0.541161616855569095758001848271evalf(-Pi^4/180,30);-0.541161616855569095758001848272ce qui paraît plutôt convaincant ! Il en va tout autrement avec chatGPT 5.2, pour qui le calcul de I se ramène à celui d’une série double « bien connue » (sic) :
![Rendered by QuickLaTeX.com \[\ln^{2}\left(1-t\right)=\sum_{m,n\geqslant1}\dfrac{t^{m+n}}{mn}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-13a26b54e2e2dce789a07956d2b8f801_l3.png)
![Rendered by QuickLaTeX.com \[\int_{0}^{1}\dfrac{\ln\left(t\right)\ln^{2}\left(1-t\right)}{t}\thinspace dt=\int_{0}^{1}\sum_{m,n\geqslant1}\dfrac{t^{m+n-1}}{mn}\ln\left(t\right)\thinspace dt=-\sum_{m,n\geqslant1}\dfrac{1}{mn\left(m+n\right)^{2}}=-\dfrac{1}{2}\zeta\left(4\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4dc4011140c804d978fffb60c946fd2c_l3.png)


C’est intéressant, merci. Juste pour compléter la rubrique calcul symbolique, j’ai fait le test avec la version 11.2 de Mathematica, qui est une version déjà ancienne. Le résultat correct, -π^4/180, est bien trouvé.
Merci pour cette précision ! Je me posais la question, mais n’ayant pas Mathematica installé sur ma machine, j’étais dans l’incapacité d’en dire plus.